专题复习检测A卷1．在△ABC中，a＝2，A＝45°，则△ABC外接圆的半径R等于()A．1B．2C．4D．无法确定【答案】A【解析】2R＝asinA＝2sin45°＝2，R＝1.2．(陕西模拟)在△ABC中，a，b，c分别是角A，B，C的对边，(a＋b＋c)(a＋c－b)＝3ac，则角B＝()A．2π3B．π3C．5π6D．π6【答案】B【解析】由(a＋b＋c)(a＋c－b)＝3ac，可得a2＋c2－b2＝ac，根据余弦定理可得cosB＝a2＋c2－b22ac＝12.又B∈(0，π)，所以B＝π3.故选B．3．(北京模拟)在△ABC中，角A，B，C所对应的边分别为a，b，c，若∠C＝30°，a＝2c，则角B等于()A．45°B．105°C．15°或105°D．45°或135°【答案】C【解析】由正弦定理asinA＝csinC，得sinA＝asinCc＝2csin30°c＝22，所以∠A＝45°或135°.所以∠B＝105°或15°.故选C．4．(陕西榆林二模)在△ABC中，角A，B，C的对边分别是a，b，c，sinAsinB＝13，若c＝2cosC＝3，则△ABC的周长为()A．3B．23C．3＋

2．9函数模型及其应用1．函数的实际应用(1)基本函数模型函数模型函数解析式一次函数模型二次函数模型指数型函数模型f(x)＝bax＋c(a，b，c为常数，a＞0且a≠1，b≠0)对数型函数模型f(x)＝blogax＋c(a，b，c为常数，a＞0且a≠1，b≠0)幂型函数模型f(x)＝axn＋b(a，b为常数，a≠0)(2)三种常用函数模型性质比较函数性质y＝ax(a＞1)y＝logax(a＞1)y＝xn(n＞0)在(0，＋∞)上的单调性单调____函数单调____函数单调____函数增长速度越来越____越来越____相对平稳图象的变化随x值增大，图象与____轴接近平行随x值增大，图象与____轴接近平行随n值变化而不同2.函数建模(1)函数模型应用的两个方面①利用已知函数模型解决问题；②建立恰当的函数模型，并利用所得函数模型解释有关现象，对某些发展趋势进行预测．(2)应用函数模型解决问题的基本过程：________、________、________、___

新高考数学实战演练仿真模拟卷一．选择题（共8小题）1．已知集合2{|560}Axxx，1{|33}xBx，则(AB)A．{|06}xxB．{|10}xxC．{|06}xx„D．{|0}xx【解析】解：{|16}Axx，{|0}Bxx，{|10}ABxx．故选：B．2．若复数z满足11iiz，其中i为虚数单位，则||(z)A．1B．2C．2D．3【解析】解：复数z满足11iiz，解得11izi，所以22221(1)|1|||1|1|11izi．故选：A．3．设等差数列{}na的前n项和为nS，若44a，972S，则10(a)A．20B．23C．24D．28【解析】解：设等差数列{}na的公差为d，44a，972S，134ad，1989722ad，解得18a，4d，则1084928a．故选：D．4．德国著名的天文学家开普勒说过：“几何学里有两件宝，一个是勾股定理，另一个是黄金分割．如果把勾股定理比作黄金矿的话，�

考点02命题及其关系、充分条件与必要条件（1）理解命题的概念.（2）了解“若p，则q”形式的命题及其逆命题、否命题与逆否命题，会分析四种命题的相互关系.（3）理解必要条件、充分条件与充要条件的意义.一、命题及其关系1．命题的概念在数学中用语言、符号或式子表达的，可以判断真假的陈述句叫做命题．其中判断为真的语句叫真命题，判断为假的语句叫假命题．2．四种命题及其关系(1)四种命题命题表述形式原命题若p，则q逆命题若q，则p否命题若p，则q逆否命题若q，则p(2)四种命题间的关系(3)常见的否定词语正面词语=>(<)是都是任意(所有)的任两个至多有1(n)个至少有1个否定词()不是不都是某个某两个至少有2(n+1)个1个也没有3．四种命题的真假关系(1)两个命题互为逆否命题，它们有相同的真假性；(2)两个命题互为逆命题或互�

专题复习检测A卷1．已知向量a＝(2,6)，b＝(－1，λ)，若a∥b，则λ＝()A．3B．－3C．13D．－13【答案】B2．已知向量a＝(x－1,2)，b＝(2,1)，则a⊥b的充要条件是()A．x＝－12B．x＝－1C．x＝5D．x＝0【答案】D3．在四边形ABCD中，AC→＝(1,2)，BD→＝(－4,2)，则该四边形的面积为()A．5B．25C．5D．10【答案】C4．(山东模拟)已知|a|＝1，|b|＝2，且a⊥(a－b)，则向量a在b方向上的投影为()A．1B．2C．12D．22【答案】D【解析】由a⊥(a－b)，可得a·(a－b)＝a2－a·b＝0，所以a·b＝a2＝1.所以向量a在b方向上的投影为|a|cos〈a，b〉＝a·b|b|＝12＝22.故选D．5．(湖南怀化模拟)在△ABC中，D为BC上一点，E是AD的中点，若BD→＝λDC→，CE→＝13AB→＋μAC→，则λ＋μ＝()A．13B．－13C．76D．－76【答案】B【解析】如图所示，由BD→＝λDC→，可得AD→－AB→＝λ(AC→－AD→)，则AD→＝11＋λAB→＋λ1＋λAC→

3．1导数的概念及运算1．导数的概念(1)定义如果函数y＝f(x)的自变量x在x0处有增量Δx，那么函数y相应地有增量Δy＝f(x0＋Δx)－f(x0)，比值ΔyΔx就叫函数y＝f(x)从x0到x0＋Δx之间的平均变化率，即ΔyΔx＝f（x0＋Δx）－f（x0）Δx.如果当Δx→0时，ΔyΔx有极限，我们就说函数y＝f(x)在点x0处____________，并把这个极限叫做f(x)在点x0处的导数，记作____________或y′|x＝x0，即f′(x0)＝0limxΔyΔx＝0limxf（x0＋Δx）－f（x0）Δx.(2)导函数当x变化时，f′(x)便是x的一个函数，我们称它为f(x)的导函数(简称导数)．y＝f(x)的导函数有时也记作y′，即f′(x)＝y′＝0limxf（x＋Δx）－f（x）Δx.(3)用定义求函数y＝f(x)在点x0处导数的方法①求函数的增量Δy＝____________；②求平均变化率ΔyΔx＝____________；③取极限，得导数f′(x0)＝0limxΔyΔx.2．导数的几何意义函数y＝f(x)在点x0�

新高考数学实战演练仿真模拟卷一．选择题（共8小题）1．已知函数()()fxxxab，若函数(1)yfx为偶函数，且f（1）0，则b的值为()A．2B．1C．1D．2【解析】解：(1)fx为偶函数，(1)(1)fxfx，(1)(1)(1)(1)xxabxxab，22(2)1(2)1xaxaxaxa，22aa，解得2a，又f（1）0，(12)0b，解得1b．故选：C．2．已知集合2{|20}Axxx„，{|1381}xBx，{|2Cxxn，}nN，则()(ABC)A．{0，2，4}B．{2，4}C．{0，2}D．{2}【解析】解：{|02}Axx剟，{|04}Bxx，{|2Cxxn，}nN，{|04}ABxx„，(){0ABC，2}．故选：C．3．若复数1zi，则||(1zz)A．1B．2C．22D．4【解析】解：数1zi，则11|||||||1|2111ziiizii，故选：B．4．已知等差数列{}na的前n项和为nS，2121aa，2a与

专题复习检测A卷1．(新课标Ⅲ)中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是()ABCD【答案】A【解析】由题意，木构件与某一带卯眼的木构件咬合成长方体，小的长方体是榫头，从图形看出轮廓是长方形，内含一个长方形，且一条边重合，另外3边是虚线．故选A．2．(北京海淀区模拟)一个正四棱锥的底面边长为2，高为3，则该正四棱锥的全面积为()A．8B．12C．16D．20【答案】B【解析】由题意得侧面三角形的高为32＋12＝2，所以该四棱锥的全面积为4×12×2×2＋22＝12.故选B．3．(四川广安模拟)已知△ABC中，AB＝AC＝2，AB⊥AC，将△ABC绕BC所在直线旋转一周，形成一个几何体，则该几�

考点03逻辑联结词、全称量词与存在量词1．简单的逻辑联结词了解逻辑联结词“或”、“且”、“非”的含义.2．全称量词与存在量词（1）理解全称量词与存在量词的意义.（2）能正确地对含有一个量词的命题进行否定.一、逻辑联结词1．常见的逻辑联结词：或、且、非一般地，用联结词“且”把命题p和q联结起来，得到一个新命题，记作pq，读作“p且q”；用联结词“或”把命题p和q联结起来，得到一个新命题，记作pq，读作“p或q”；对一个命题p的结论进行否定，得到一个新命题，记作p，读作“非p”．2．复合命题的真假判断“p且q”“p或q”“非p”形式的命题的真假性可以用下面的表（真值表）来确定：pqpqpqpq()pq()pq()()pq()()pq真真假假真真假假假假真假假真真假假真真假假真真假真假假真真假假假真真假假�

3．2导数的应用(一)函数的单调性与导数(1)在某个区间(a，b)内，如果f′(x)>0，那么函数y＝f(x)在这个区间内________；如果f′(x)<0，那么函数y＝f(x)在这个区间内________．(2)如果在某个区间内恒有f′(x)＝0，那么函数f(x)在这个区间上是________．自查自纠：(1)单调递增单调递减(2)常数函数(教材改编)函数f(x)＝x3－6x2的单调递减区间为()A．(0，4)B．(0，2)C．(4，＋∞)D．(－∞，0)解：f′(x)＝3x2－12x＝3x(x－4)，由f′(x)<0，得0<x<4，所以单调递减区间为(0，4)．故选A.已知函数f(x)＝1＋x－sinx，则f(2)，f(3)，f(π)的大小关系正确的是()A．f(2)>f(3)>f(π)B．f(3)>f(2)>f(π)C．f(2)>f(π)>f(3)D．f(π)>f(3)>f(2)解：f′(x)＝1－cosx，当x∈(0，π]时，f′(x)>0，所以f(x)在(0，π]上是增函数，所以f(π)>f(3)>f(2)．故选D.(2017·浙江)函数y＝f(x)的导函数y＝f′(x)的图象如图所示，则函数y＝f(x)的图象可能是

新高考数学实战演练仿真模拟卷一．选择题（共8小题）1．已知集合2{|60}Axxx„，{|10}Bxx，则(AB)A．(，3]B．(，2]C．(,1)D．[2，1)【解析】解：集合2{|60}{|23}Axxxxx剟?，{|10}{|1}Bxxxx，{|3}(ABxx„，3]．故选：A．2．复数2(1)(1ii)A．1iB．1iC．1iD．1i【解析】解：复数22(1)1222(1)111(1)(1)iiiiiiiiiii222211iiii．故选：C．3．如图是一个装有水的倒圆锥形杯子，杯子口径6cm，高8cm（不含杯脚），已知水的高度是4cm，现往杯子中放入一种直径为1cm的珍珠，该珍珠放入水中后直接沉入杯底，且体积不变．如果放完珍珠后水不溢出，则最多可以放入珍珠()A．98颗B．106颗C．120颗D．126颗【解析】解：作出轴截面如图，由题意，8OP，14OP，3OA，设11OAx

专题复习检测A卷1．△ABC所在的平面为α，直线l⊥AB，l⊥AC，直线m⊥BC，m⊥AC，则直线l，m的位置关系是()A．相交B．异面C．平行D．不确定【答案】C【解析】l⊥AB，l⊥AC⇒l⊥α；m⊥BC，m⊥AC⇒m⊥α.故l∥m.2．已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是()A．若m⊥α，n⊥α，则m∥nB．若α⊥γ，β⊥γ，则α∥βC．若m∥α，n∥α，则m∥nD．若m∥α，m∥β，则α∥β【答案】A【解析】垂直于同一个平面的两条直线平行，A正确；α，β垂直于同一个平面γ，则α，β可能相交或平行，B错误；m，n平行于同一个平面，则m，n可能相交、平行或异面，C错误；α，β平行于同一条直线m，则α，β可能相交或平行，D错误．故选A．3．(福建三明二模)如图，已知正方体ABCD－A1B1C1D1的棱长为2，则以下四个命题中错误的是()A．直线A1C1与AD1为异面直线B�

考点04函数及其表示（1）了解构成函数的要素，会求一些简单函数的定义域和值域；了解映射的概念.（2）在实际情境中，会根据不同的需要选择恰当的方法（如图象法、列表法、解析法）表示函数.（3）了解简单的分段函数，并能简单应用.一、函数的概念1．函数与映射的相关概念(1)函数与映射的概念函数映射两个集合A、B设A、B是两个非空数集设A、B是两个非空集合对应关系按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应按某一个确定的对应关系f，使对于集合A中的任意一个元素x，在集合B中都有唯一确定的元素y与之对应名称称f：A→B为从集合A到集合B的一个函数称f：A→B为从集合A到集合B的一个映射记法y＝f(x)，x∈Af：A→B注意：判断一个对应关系是否是函数关系，就看这个对应关系是否满足函�

3．3导数的应用(二)1．函数的极值与导数(1)判断f(x0)是极大值，还是极小值的方法一般地，当f′(x0)＝0时，①如果在x0附近的左侧f′(x)＞0，右侧f′(x)＜0，那么f(x0)是极大值；②如果在x0附近的左侧____________，右侧____________，那么f(x0)是极小值．(2)求可导函数极值的步骤①求f′(x)；②求方程____________的根；③检查f′(x)在上述根的左右对应函数值的符号．如果左正右负，那么f(x)在这个根处取得____________；如果左负右正，那么f(x)在这个根处取得____________．2．函数的最值与导数(1)在闭区间[a，b]上连续的函数f(x)在[a，b]上必有最大值与最小值．(2)若函数f(x)在[a，b]上单调递增，则____________为函数在[a，b]上的最小值，____________为函数在[a，b]上的最大值；若函数f(x)在[a，b]上单调递减，则____________为函数在[a，b]上的最大值，____________为函数在[a，b]上的最小�

新高考数学实战演练仿真模拟卷一．选择题（共8小题）1．已知集合2{|20}Axxx，{|1}Bxxm，ABA，则实数m的取值范围为()A．(2,)B．(1,2)C．[2，)D．(1，2]【解析】解：{|12}Axx；ABA；AB；2m…；m的取值范围为[2，)．故选：C．2．已知复数(12)(2)Zii（其中i为虚数单位），则复数Z的共轭复数在复平面内对应的点为()A．(3,4)B．(3,4)C．(4,3)D．(4,3)【解析】解：2(12)(2)24243Ziiiiii，43Zi，则复数Z的共轭复数在复平面内对应的点为(4,3)，故选：D．3．“22mn”是“lnmlnn”()A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分又不必要条件【解析】解：lnmlnn，则0mn，故22mn，反之，22mn，得||||mn，推不出lnmlnn，故“22mn”是“lnmlnn”的必要不充分条件�

专题复习检测A卷1．在空间四边形OABC中，OB＝OC，∠AOB＝∠AOC＝π3，则cos〈OA→，BC→〉等于()A．12B．22C．－12D．0【答案】D【解析】OA→·BC→＝OA→·(OC→－OB→)＝OA→·OC→－OA→·OB→＝|OA→|·|OC→|cos〈OA→，OC→〉－|OA→|·|OB→|cos〈OA→，OB→〉＝|OA→|·|OC→|cosπ3－|OA→|·|OB→|cosπ3＝0，∴cos〈OA→，BC→〉＝0.2．已知长方体ABCD－A1B1C1D1中，AB＝BC＝4，CC1＝2，则直线BC1和平面DBB1D1夹角的正弦值为()A．32B．33C．105D．1010【答案】C【解析】如图，建立空间直角坐标系，则B(4,0,0)，C(4,4,0)，C1(4,4,2)，显然AC⊥平面BB1D1D，所以AC→＝(4,4,0)为平面BB1D1D的一个法向量．又BC1→＝(0,4,2)，所以cos〈BC1→，AC→〉＝BC1→·AC→|BC1→||AC→|＝1616＋4·16＋16＝105，即直线BC1和平面DBB1D1夹角的正弦值为105.3．已知三棱柱ABC－A1B1C1的侧棱与底面垂直，体积为94，底面是边长为3的正三�

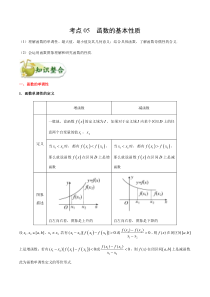
考点05函数的基本性质（1）理解函数的单调性、最大值、最小值及其几何意义；结合具体函数，了解函数奇偶性的含义.（2）会运用函数图象理解和研究函数的性质.一、函数的单调性1．函数单调性的定义增函数减函数定义一般地，设函数fx的定义域为I，如果对于定义域I内某个区间D上的任意两个自变量的值1x，2x当12xx时，都有12fxfx，那么就说函数fx在区间D上是增函数当12xx时，都有12fxfx，那么就说函数fx在区间D上是减函数图象描述自左向右看，图象是上升的自左向右看，图象是下降的设12,[,]xxab，12xx.若有1212()0[]xxfxfx或1212()()0fxfxxx，则()fx在闭区间[],ab上是增函数；若有1212()0[]xxfxfx或1212()()0fxfxxx，则()fx在闭区间[],ab上是减函数.此为函数单调性定义的等价形式.2．�

4．1弧度制及任意角的三角函数1．任意角(1)角的概念角可以看成平面内一条射线绕着端点从一个位置______到另一个位置所成的图形．我们规定：按____________方向旋转形成的角叫做正角，按____________方向旋转形成的角叫做负角．如果一条射线没有作任何旋转，我们称它形成了一个____________．(2)象限角使角的顶点与原点重合，角的始边与x轴的____________重合．角的终边在第几象限，就说这个角是第几象限角．①α是第一象限角可表示为α|2kπ<α<2kπ＋π2，k∈Z；②α是第二象限角可表示为____________；③α是第三象限角可表示为____________；④α是第四象限角可表示为____________．(3)非象限角如果角的终边在____________上，就认为这个角不属于任何一个象限．①终边在x轴非负半轴上的角的集合可记作{α|α＝2kπ，k∈Z}；②终边在x轴非正半轴上的角的集�

专题复习检测A卷1．(天津模拟)8名学生和2位老师站成一排合影，2位老师不相邻的排法种数为()A．A88A29B．A88C29C．A88A27D．A88C27【答案】A【解析】不相邻问题用插空法，8名学生先排有A88种排法，产生9个空，2位老师插空有A29种排法，所以共有A88A29种排法．故选A．2．现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动，每人从事翻译、导游、礼仪、司机四项工作之一，每项工作至少有一人参加．甲、乙不会开车但能从事其他三项工作，丙、丁、戊都能胜任四项工作，则不同安排方案的种数是()A．152B．126C．90D．54【答案】B【解析】分两类：若有2人从事司机工作，则有C23A33＝18种；若有1人从事司机工作，则有C13C24A33＝108种，所以共有18＋108＝126种．3．(广西钦州三模)二项式x＋12xn的展开式前三项系数成等差数列，则n＝()A．6B．7C�

新高考数学实战演练仿真模拟卷一．选择题（共8小题）1．满足条件|1||34|zi的复数z在复平面上对应点的轨迹是()A．直线B．圆C．椭圆D．抛物线【解析】解：设zxyi，由|1||34|zi，可得|(1)||34|xyii，即2222(1)34xy，两边同平方可得22(1)25xy，所以复数z在复平面上对应点的轨迹是以(1,0)为圆心，5为半径的圆．故选：B．2．在二项式10(1)x的展开式中任取一项，则该项的系数为奇数的概率是()A．25B．411C．511D．611【解析】解：有题意知本题是一个等可能事件的概率，在二项式10(1)x的展开式中任取一项有11种结果，1和x系数都为1，我们只考虑二项式系数即可．二项式系数为1，10，45，120，210，252，210，120，45，10，1得到奇数4个，任取一项，该项的系数为奇数的概率411p故选：B．3．化学平衡是指在一定条件下，可逆反应