考点24不等关系与一元二次不等式1．不等关系了解现实世界和日常生活中的不等关系，了解不等式（组）的实际背景.2．一元二次不等式（1）会从实际情境中抽象出一元二次不等式模型.（2）通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.（3）会解一元二次不等式，对给定的一元二次不等式，会设计求解的程序框图.一、不等关系1．不等式的概念（1）现实世界与日常生活中，与等量关系一样，不等量关系也是自然界中存在着的基本数量关系．（2）用数学符号“”“”“”“”连接两个数或代数式以表示它们之间的不等关系，含有这些不等号的式子，叫做不等式．2．两个实数大小的比较（1）作差法：设a，bR，则0abab，a<b⇔a−b<0.（2）作商法：设a>0，b>0，则a>b⇔1ab，a<b⇔1ab.3．不等式的性质（1）�

18．4空间中的平行关系1．空间中直线与平面之间的位置关系(1)直线在平面内，则它们__________公共点．(2)直线与平面相交，则它们______________公共点．(3)直线与平面平行，则它们________公共点．直线与平面相交或平行的情况统称为______________．2．直线与平面平行的判定和性质(1)直线与平面平行的判定定理平面外____________与此平面内的____________平行，则该直线与此平面平行．即线线平行⇒线面平行．用符号表示：____________________________．(2)直线与平面平行的性质定理一条直线与一个平面平行，则过这条直线的任一平面与此平面的__________与该直线__________．即线面平行⇒线线平行．用符号表示：__________________________．3．平面与平面之间的位置关系(1)两个平面平行，则它们______________．(2)两个平面相交，则它们______________，两个平面垂直是相交的一种特殊情

考点25二元一次不等式（组）与简单的线性规划问题（1）会从实际情境中抽象出二元一次不等式组.（2）了解二元一次不等式的几何意义，能用平面区域表示二元一次不等式组.（3）会从实际情境中抽象出一些简单的二元线性规划问题，并能加以解决.一、二元一次不等式（组）与平面区域1．二元一次不等式表示的平面区域一般地，在平面直角坐标系中，二元一次不等式0AxByC表示直线0AxByC某一侧所有点组成的平面区域，我们把直线画成虚线，以表示区域不包括边界.不等式0AxByC表示的平面区域包括边界，把边界画成实线．2．对于二元一次不等式的不同形式，其对应的平面区域有如下结论：3．确定二元一次不等式(组)表示平面区域的方法（1）对于直线0AxByC同一侧的所有点(x，y)，使得AxByC的值符号相同，也就是位于同一�

18．5空间中的垂直关系1．线线垂直如果两条直线所成的角是______(无论它们是相交还是异面)，那么这两条直线互相垂直．2．直线与平面垂直(1)定义：如果直线l与平面α内的任意一条直线都垂直，我们就说______________________，记作______．直线l叫做______________，平面α叫做______________．直线与平面垂直时，它们惟一的公共点P叫做______．垂线上任意一点到垂足间的线段，叫做这个点到这个平面的垂线段，垂线段的长度叫做这个点到平面的________．(2)判定定理：一条直线与一个平面内的______________都垂直，则该直线与此平面垂直．推论：如果在两条平行直线中，有一条垂直于平面，那么另一条直线也垂直于这个平面．用符号表示：a∥b，a⊥α⇒b⊥α．(3)性质定理：垂直于同一个平面的两条直线__________．3．直线和平面所成的角平面的一条斜线和它在平面上的�

考点26基本不等式基本不等式：(0,0)2ababab（1）了解基本不等式的证明过程.（2）会用基本不等式解决简单的最大（小）值问题.一、基本不等式1．基本不等式：2abab（1）基本不等式成立的条件：0,0ab.（2）等号成立的条件，当且仅当ab时取等号．2．算术平均数与几何平均数设0,0ab，则a、b的算术平均数为2ab，几何平均数为ab，基本不等式可叙述为：两个正数的算术平均数不小于它们的几何平均数．3．利用基本不等式求最值问题（1）如果积xy是定值P，那么当且仅当xy时，x＋y有最小值是2P.(简记：积定和最小)（2）如果和x＋y是定值P，那么当且仅当xy时，xy有最大值是24P.(简记：和定积最大)4．常用结论（1）222(,)abababR（2）2(,)baabab同号（3）2()(,)2abababR（4）222()(,)22abababR（5）2222()()(,)abababR（6

18．6空间向量及其加减、数乘和数量积运算1．空间向量的有关概念(1)空间向量：在空间，我们把具有________和________的量叫做空间向量．(2)零向量：规定______________的向量叫做零向量．(3)单位向量：________的向量称为单位向量．(4)相反向量：与向量a__________________的向量，称为a的相反向量，记为－a．(5)相等向量：________________的向量称为相等向量．(6)空间向量的加法运算满足交换律及结合律：a＋b＝________；(a＋b)＋c＝______________．2．空间向量的数乘运算(1)向量的数乘：实数λ与空间向量a的乘积λa仍然是一个向量，称为向量的数乘．①当λ____0时，λa与向量a方向相同；当λ____0时，λa与向量a方向相反．②λa的长度是向量a的长度的______倍．(2)空间向量的数乘运算满足分配律及结合律：①分配律：λ(a＋b)＝____________．②结合律：λ(μa)＝________．(3)共线向量�

考点27空间几何体的结构及其三视图与直观图空间几何体（1）认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构.（2）能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别上述三视图所表示的立体模型，会用斜二测法画出它们的直观图.（3）会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式.（4）会画某些建筑物的视图与直观图（在不影响图形特征的基础上，尺寸、线条等不作严格要求）.一、空间几何体的结构1．多面体几何体结构特征备注棱柱①底面互相平行.②侧面都是平行四边形③每相邻两个平行四边形的公共边互相平行.按侧棱与底面是否垂直分类，可分为斜棱柱和直棱柱.侧棱与底面不垂直的棱柱叫做斜�

18．7空间向量的坐标表示、运算及应用1．空间向量基本定理如果三个向量a，b，c不共面，那么对空间任一向量p，存在有序实数组____________，使得__________________．其中，{a，b，c}叫做空间的一个________，a，b，c都叫做__________．2．空间直角坐标系(1)如果空间的一个基底的三个基向量____________，且长都为______，则这个基底叫做单位正交基底，常用{i，j，k}来表示(其中|i|＝|j|＝|k|＝1)．(2)在空间选定一点O和一个单位正交基底{}i，j，k，以O为原点，分别以i，j，k的方向为正方向建立三条数轴：__________________________，它们都叫做坐标轴，这时我们说建立了一个空间直角坐标系Oxyz，点O叫做原点，向量i，j，k都叫做坐标向量．通过每两个坐标轴的平面叫做坐标平面，分别称为xOy平面、yOz平面、zOx平面．(3)建系时，一般使∠xOy＝135°(或45°)，∠yOz＝90°，建立____手

19．1直线与方程1．平面直角坐标系中的基本公式(1)数轴上A，B两点的距离数轴上点A的坐标为x1，点B的坐标为x2，则A，B两点间的距离|AB|＝____________．(2)平面直角坐标系中的基本公式①两点间的距离公式：在平面直角坐标系中，两点A(x1，y1)，B(x2，y2)之间的距离公式为d(A，B)＝|AB|＝_________________________．②线段的中点坐标公式：若点P1，P2的坐标分别为(x1，y1)，(x2，y2)，线段P1P2的中点M的坐标为(x，y)，则x＝，y＝．2．直线的倾斜角与斜率(1)直线的倾斜角当直线l与x轴相交时，取x轴作为基准，x轴________与直线l向上方向之间所成的角α叫做直线l的倾斜角．当直线l与x轴________或________时，我们规定它的倾斜角为0°．因此，直线的倾斜角α的取值范围为__________________．(2)斜率一条直线的倾斜角α的____________叫做这条直线的斜率，常用小写字母k表示，

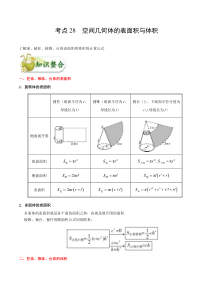
考点28空间几何体的表面积与体积了解球、棱柱、棱锥、台的表面积和体积的计算公式.一、柱体、锥体、台体的表面积1．旋转体的表面积圆柱（底面半径为r，母线长为l）圆锥（底面半径为r，母线长为l）圆台（上、下底面半径分别为r′,r,母线长为l）侧面展开图底面面积2π底Sr2π底Sr22,ππ上底下底SrSr侧面面积2π侧Srlπ侧Srlπ侧Slrr表面积2π表Srrlπ表Srrl22π表Srrrlrl2．多面体的表面积多面体的表面积就是各个面的面积之和，也就是展开图的面积.棱锥、棱台、棱柱的侧面积公式间的联系：二、柱体、锥体、台体的体积1．柱体、锥体、台体的体积公式几何体体积柱体柱体VSh(S为底面面积，h为高),2π圆柱Vrh(r为底面半径，h为高)锥体13锥体VSh(S为底面面积，h为高)，213π圆锥Vrh(r为底面半径

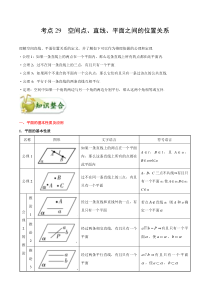
考点29空间点、直线、平面之间的位置关系理解空间直线、平面位置关系的定义，并了解如下可以作为推理依据的公理和定理.·公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在此平面内.·公理2：过不在同一条直线上的三点，有且只有一个平面.·公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.·公理4：平行于同一条直线的两条直线互相平行.·定理：空间中如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补.一、平面的基本性质及应用1．平面的基本性质名称图形文字语言符号语言公理1如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在此平面内Al，Bl，且Aα，Bα⇒l⊂α公理2过不在同一条直线上的三点，有且只有一个平面A，B，C三点不共�

19．2两条直线的位置关系1．两条直线的位置关系(1)平行：对于两条不重合的直线l1，l2，其斜率分别为k1，k2，有l1∥l2⇔____________，特别地，当直线l1，l2的斜率都不存在时，l1与l2的关系为____________．(2)垂直：如果两条直线l1，l2的斜率都存在，且分别为k1，k2，则有l1⊥l2⇔____________，特别地，若直线l1：x＝a，直线l2：y＝b，则l1与l2的关系为____________．2．两条直线的交点坐标一般地，将两条直线的方程联立，得方程组A1x＋B1y＋C1＝0，A2x＋B2y＋C2＝0．若方程组有唯一解，则两条直线__________，此解就是__________；若方程组无解，则两条直线____________，此时两条直线____________．3．距离公式(1)点到直线的距离：点P0(x0，y0)到直线l：Ax＋By＋C＝0的距离d＝_____________________．(2)两条平行直线间的距离：两条平行直线l1：Ax＋By＋C1＝0与l2：Ax＋By＋C2＝0(C1�

考点30直线、平面平行的判定及其性质（1）以立体几何的定义、公理和定理为出发点，认识和理解空间中线面平行的有关性质与判定定理.理解以下判定定理：·如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行.·如果一个平面内的两条相交直线与另一个平面都平行，那么这两个平面平行.理解以下性质定理，并能够证明：·如果一条直线与一个平面平行，那么经过该直线的任一个平面与此平面的交线和该直线平行.·如果两个平行平面同时和第三个平面相交，那么它们的交线相互平行.·垂直于同一个平面的两条直线平行.（2）能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.一、直线与平面平行的判定与性质1．直线与平面平行的判定定理文字语言平面外的一条直线与此平面内的一条直线平行，则该直

19．3圆的方程1．圆的定义在平面内，到____________的距离等于____________的点的____________叫圆．确定一个圆最基本的要素是____________和____________．2．圆的标准方程与一般方程(1)圆的标准方程：方程(x－a)2＋(y－b)2＝r2(r>0)叫做以点____________为圆心，____________为半径长的圆的标准方程．(2)圆的一般方程：方程x2＋y2＋Dx＋Ey＋F＝0(____________)叫做圆的一般方程．注：将上述一般方程配方得x＋D22＋y＋E22＝D2＋E2－4F4，此为该一般方程对应的标准方程，表示的是以____________为圆心，____________为半径长的圆．3．点与圆的位置关系点与圆的位置关系有三种，设圆的标准方程(x－a)2＋(y－b)2＝r2(r>0)，点M(x0，y0)，则(1)点M在圆上：_________________________．(2)点M在圆外：_________________________．(3)点M在圆内：_________________________．4．确定圆的方程的方法和步骤确�

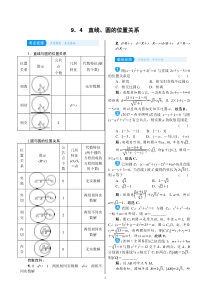
19．4直线、圆的位置关系1．直线与圆的位置关系位置关系图示公共点个数几何特征代数特征(解的个数)相离无实数解相切d＝r相交22.圆与圆的位置关系位置关系图示(R>r)公共点个数几何特征(O1O2＝d)代数特征(两个圆的方程组成的方程组的解的个数)外离0无实数解外切1两组相同实数解相交2两组不同实数解内切1两组相同实数解内含0无实数解自查自纠：1．0d>r1两组相同实数解d<r两组不同实数解2．d>R＋rd＝R＋rR－r<d<R＋rd＝R－rd<R－r圆(x－1)2＋(y＋2)2＝6与直线2x＋y－5＝0的位置关系是()A．相切B．相交但直线不过圆心C．相交过圆心D．相离解：由题意知圆心(1，－2)到直线2x＋y－5＝0的距离d＝|2×1－2－5|22＋1＝5<6，且2×1＋(－2)－5≠0，所以直线与圆相交但不过圆心．故选B．(2017·西安调研)若直线x－y＋1＝0与圆(x－a)2＋y2＝2有公共点，则实数a的取值范围是()A．[－

考点31直线、平面垂直的判定及其性质（1）以立体几何的定义、公理和定理为出发点，认识和理解空间中线面垂直的有关性质与判定定理.理解以下判定定理：·如果一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直.·如果一个平面经过另一个平面的垂线，那么这两个平面互相垂直.理解以下性质定理，并能够证明：·如果两个平面垂直，那么一个平面内垂直于它们交线的直线与另一个平面垂直.（2）能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.一、直线与平面垂直1．定义如果直线l与平面α内的任意一条直线都垂直，我们就说直线l与平面α互相垂直.记作：l⊥α.图形表示如下：【注意】定义中的“任意一条直线”这一词语与“所有直线”是同义语，与“无数条直线”不是同义语．2．直线与平面垂直

19．5曲线与方程1．曲线与方程一般地，在直角坐标系中，如果某曲线C(看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程f(x，y)＝0的实数解建立了如下的关系：(1)____________________________________．(2)____________________________________．那么，这个方程叫做曲线的方程，这条曲线叫做方程的曲线．2．求曲线方程的一般步骤(1)建立适当的__________，用有序实数对(x，y)表示曲线上____________M的坐标．(2)写出____________的点M的集合：P＝{M|p(M)}．(3)用__________表示条件p(M)，列出方程f(x，y)＝0．(4)化方程f(x，y)＝0为____________形式．(5)说明以化简后的方程的________为坐标的________都在曲线上．注：步骤(5)可以省略不写，如有特殊情况，可以作适当说明，另外，也可以根据情况省略步骤(2)．3．求曲线的轨迹方程的常用方法(1)直接法：直接利用条件建立x，y之间的关�

考点32直线与方程（1）在平面直角坐标系中，结合具体图形，确定直线位置的几何要素.（2）理解直线的倾斜角和斜率的概念，掌握过两点的直线斜率的计算公式.（3）掌握直线方程的几种形式（点斜式、两点式及一般式），了解斜截式与一次函数的关系.一、直线的倾斜角与斜率1．直线的倾斜角（1）定义：在平面直角坐标系中，对于一条与x轴相交的直线，把x轴所在的直线绕着交点按逆时针方向旋转到和直线重合时所转过的最小正角称为这条直线的倾斜角．当直线l与x轴平行或重合时，规定它的倾斜角为0．（2）范围：直线l倾斜角的范围是[0,180)．2．斜率公式（1）若直线l的倾斜角90°，则斜率tank．（2）P1(x1，y1)，P2(x2，y2)在直线l上，且x1≠x2，则直线l的斜率k＝2121yyxx．二、直线的方程1．直线方程的五种形式方程适用范围①点�

19．6椭圆1．椭圆的定义(1)定义：平面内与两个定点F1，F2的距离的和等于常数2a(2a______|F1F2|)的点的轨迹叫做椭圆．这两个定点叫做椭圆的________，两焦点间的距离叫做椭圆的________．※(2)另一种定义方式(见人教A版教材选修2－1P47例6、P50)：平面内动点M到定点F的距离和它到定直线l的距离之比等于常数e(0＜e＜1)的轨迹叫做椭圆．定点F叫做椭圆的一个焦点，定直线l叫做椭圆的一条准线，常数e叫做椭圆的__________．2．椭圆的标准方程及几何性质焦点在x轴上焦点在y轴上(1)图形(2)标准方程y2a2＋x2b2＝1(a>b>0)(3)范围－a≤x≤a，－b≤y≤b－a≤y≤a，－b≤x≤b(4)中心原点O(0，0)(5)顶点A1(－a，0)，A2(a，0)B1(0，－b)，B2(0，b)(6)对称轴x轴，y轴(7)焦点F1(0，－c)，F2(0，c)(8)焦距2c＝2a2－b2(9)离心率自查自纠：1．(1)＞焦点焦距(2)离心率2．(2)x2a2＋y2b2＝1(a＞b＞0)(5)A1(0，－a)，A2(0�

考点33直线的位置关系（1）能根据两条直线的斜率判定这两条直线平行或垂直.（2）能用解方程组的方法求两条相交直线的交点坐标.（3）掌握两点间的距离公式、点到直线的距离公式，会求两条平行直线间的距离.一、两条直线的位置关系斜截式111222::lykxblykxb一般式11112222:0:0lAxByClAxByC1l与2l相交12kk12210ABAB1l与2l垂直121kk12120AABB1l与2l平行12kk且12bb1221122100ABABBCBC或1221122100ABABACAC1l与2l重合12kk且12bb1221122112210ABABACACBCBC注意：（1）当两条直线平行时，不要忘记它们的斜率不存在时的情况；（2）当两条直线垂直时，不要忘记一条直线的斜率不存在、另一条直线的斜率为零的情况．二、两条直线的交点对于直线l1：A1x＋B1y＋C1＝0，l2：A2x＋B2y＋C2＝0，1l与2l的交点坐标�