第2节平面向量基本定理及向量坐标运算【教材回扣】1．平面向量基本定理(1)基底：________的向量e1，e2叫做表示这一平面内所有向量的一组基底．(2)定理：如果e1，e2是同一平面内的两个________向量，那么对于这一平面内的任意向量a，有且只有一对实数λ1，λ2，使a＝________.2．平面向量的坐标表示在平面直角坐标系中，分别取与x轴、y轴方向相同的两个单位向量i，j作为基底，该平面内的任一向量a可表示成a＝xi＋yj，a与数对(x，y)是一一对应的，把有序数对(x，y)叫做向量a的坐标，记作a＝_____，其中a在x轴上的坐标是x，a在y轴上的坐标是y.不共线不共线(x，y)λ1e1＋λ2e23．平面向量的坐标运算向量的加法、减法设a＝(x1，y1)，b＝(x2，y2)，则a＋b＝____________，a－b＝____________向量的数乘设a＝(x，y)，λ∈R，则λa＝____________向量坐标的求法设A(x1，y1)，B(x2，y2)，则|AB→|＝________________4.向量共线的坐标表示若a＝(x1，y1)，b＝(x2，y2)，则a∥b⇔____________＝0.(x1＋x2，y1＋y2)(x1－x2，y1－y2)(λx，λy)(x2－x1)2＋(y2－y1)2x1y2－x2y1【教材提炼】一、教材改编1．[必修二·P36习题6.3T4改编]已知▱ABCD的顶点A(－1，－2)，B(3，－1)，C(5,6)，则顶点D的坐标为()A．(1,5)B．(2,5)C．(3,4)D．(5,1)答案：A解析：设顶点D的坐标为(x，y)，AB→＝(4,1)，DC→＝(5－x,6－y)，∵平行四边形ABCD中，AB→＝CD→，∴4＝5－x，1＝6－y，解得x＝1，y＝5.所以顶点D的坐标为(1,5)．2．[必修二·P36习题6.3T1改编]如图，在△ABC中，AD＝13AB，点E是CD的中点．设AB→＝a，AC→＝b，用a，b表示CD→＝________，AE→＝________.答案：13a－b，16a＋12b解析：CD→＝CA→＋AD→＝CA→＋13AB→＝－AC→＋13AB→＝13a－bAE→＝AC→＋CE→＝AC→＋12CD→＝AC→＋12(AD→－AC→)＝12AC→＋12AD→＝12AC→＋12×13

第3课时导数与不等式题型一不等式恒成立问题[师生共研][例1][2020·山东泰安一中联考]已知函数f(x)＝12x2－alnx＋1(a∈R)．(1)若函数f(x)在[1,2]上是单调递增函数，求实数a的取值范围；(2)若－2≤a<0，对任意x1，x2∈[1,2]，不等式|f(x1)－f(x2)|≤m1x1－1x2恒成立，求实数m的取值范围．解：(1)易知f(x)不是常值函数，∵f(x)＝12x2－alnx＋1在[1,2]上是增函数，∴f′(x)＝x－ax≥0恒成立，所以a≤x2，只需a≤(x2)min＝1.(2)因为－2≤a<0，由(1)知，函数f(x)在[1,2]上单调递增，不妨设1≤x1≤x2≤2，则|f(x1)－f(x2)|≤m1x1－1x2，可化为f(x2)＋mx2≤f(x1)＋mx1，设h(x)＝f(x)＋mx＝12x2－alnx＋1＋mx，则h(x1)≥h(x2)，所以h(x)为[1,2]上的减函数，即h′(x)＝x－ax－mx2≤0在[1,2]上恒成立，等价于m≥x3－ax在[1,2]上恒成立，设g(x)＝x3－ax，所以m≥g(x)max，因－2≤a<0，所以g′(x)＝3x2－a>0，所以函数g(x)在[1,2]上是增函数，所以g(x)max＝g(2)＝8－2a≤12(当且仅当a＝－2时等号成立)．所以m≥12.类题通法不等式恒成立问题的求解策略(1)已知不等式f(x·λ)>0(λ为实参数)对任意的x∈D恒成立，求参数λ的取值范围．利用导数解决此类问题可以运用分离参数法．(2)如果无法分离参数，可以考虑对参数或自变量进行分类讨论求解，如果是二次不等式恒成立的问题，可以考虑二次项系数与判别式的方法(a>0，Δ<0或a<0，Δ<0)求解.【跟踪训练1】[2020·山东莱州一中质量检测]已知函数f(x)＝1＋ln(1＋x)x(x>0)．(1)判断函数f(x)在(0，＋∞)上的单调性；(2)若f(x)>kx＋1恒成立，求整数k的最大值．解：(1)因为f(x)＝1＋ln(1＋x)x(x>0)，所以f′(x)＝－11＋x－ln(1＋x)x2，(x>0)，又因为x>0，所以11＋x>0，ln(1＋x)>0，所以f′(x)<0，即函数f(x)在(0，＋∞)上为减函数．(2)由f(x)>kx＋1恒成立，即k<x＋1＋(x＋1)ln(x＋1)

高考必考题突破讲座(一)函数与导数的综合问题高考总复习·数学（理科）题型特点考情分析命题趋势2018·全国卷Ⅰ，212018·全国卷Ⅱ，212017·全国卷Ⅰ，212017·全国卷Ⅱ，211.极值、最值、导数几何意义及单调性的综合问题．2．利用导数研究不等式的综合问题.分值：12～14分1.以函数为载体，以导数为解题工具，主要考查函数的单调性、极值、最值问题的求法，以及参数的取值范围问题．2．不等式的证明问题是高考考查的热点内容，常与不等式、二次函数等相联系．问题的解决通常采用构造新函数的方法.目录高考必考题突破讲座题型一利用导数研究函数的性质以含参数的函数为载体，结合具体函数与导数的几何意义，研究函数的性质，是高考的热点．主要考查：(1)讨论函数的单调性和单调区间；(2)求函数的极值或最值；(3)利用函数的单调性、极值、最值，求参数的范围．【例1】已知函数f(x)＝ax－2x－3lnx，其中a为常数．(1)当函数f(x)的图象在点23，f23处的切线的斜率为1时，求函数f(x)在32，3上的最小值；(2)若函数f(x)在区间(0，＋∞)上既有极大值又有极小值，求a的取值范围．解析(1)f′(x)＝a＋2x2－3x，由f′23＝a＋92－92＝1可得a＝1，即f(x)＝x－2x－3lnx，f′(x)＝1＋2x2－3x＝x2－3x＋2x2＝(x－1)(x－2)x2，当x∈32，3有：x32，22(2,3]f′(x)－0＋f(x)单调递减1－3ln2单调递增从而在32，3上，f(x)有最小值，且最小值为f(2)＝1－3ln2.(2)f′(x)＝a＋2x2－3x＝ax2－3x＋2x2(x>0)，由题设可得方程ax2－3x＋2＝0有两个不等的正实根．不妨设这两个根为x1，x2，且x1≠x2，则Δ＝9－8a＞0，x1＋x2＝3a>0，x1x2＝2a>0解得0<a<98.故所求a的取值范围为0，98.素养解读(1)从已知切线的斜率去求参数a的过程既考查了数学运算的核心素养，又考查了逻辑推理的核心素养．(2)将函数有极大值和极小值转化为一元二次方程的实数根的问题考查了数学建模的核心素养．(3)通过二次函数的图象与性质列出一元二次方程根的

5.3平面向量的数量积与平面向量的应用第五章内容索引0102必备知识预案自诊关键能力学案突破03素养提升微专题5数学运算——平面向量与三角形的“四心”必备知识预案自诊【知识梳理】1.平面向量的数量积2.向量数量积的运算律交换律a·b=b·a分配律(a+b)·c=a·c+b·c数乘结合律(λa)·b=λ(a·b)=a·(λb)(λ为实数)定义设两个非零向量a,b的夹角为θ,则数量|a||b|cosθ叫做a与b的数量积,记作a·b投影|a|cosθ叫做向量a在b方向上的投影,|b|cosθ叫做向量b在a方向上的投影几何意义数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积3.平面向量数量积的性质及坐标表示已知非零向量a=(x1,y1),b=(x2,y2),a与b的夹角为θ.向量的有关概念几何表示坐标表示模|a|=𝑎·𝑎|a|=𝑥12+𝑦12数量积|a||b|cosθx1x2+y1y2夹角cosθ=𝑎·𝑏|𝑎||𝑏|cosθ=𝑥1𝑥2+𝑦1𝑦2𝑥12+𝑦12·𝑥22+𝑦22A(x1,y1),B(x2,y2)两点的距离|AB|=|𝐴𝐵||AB|=(𝑥1-𝑥2)2+(𝑦1-𝑦2)2a⊥b的充要条件a·b=0x1x2+y1y2=0|a·b|与|a||b|的关系|a·b|≤|a||b||x1x2+y1y2|≤𝑥12+𝑦12·𝑥22+𝑦224.向量在平面几何中的应用(1)要证AB=CD,可转化为证明𝐴𝐵2=𝐶𝐷2或|𝐴𝐵|=|𝐶𝐷|.(2)要证两线段AB,CD平行,只要证存在唯一实数λ≠0,使等式𝐴𝐵=λ𝐶𝐷成立即可.(3)要证两线段AB,CD垂直,只需证𝐴𝐵·𝐶𝐷=0.(4)求夹角问题,利用夹角公式cosθ=𝑎·𝑏|𝑎||𝑏|.常用结论1.平面向量数量积运算的常用公式:(1)(a+b)·(a-b)=a2-b2.(2)(a±b)2=a2±2a·b+b2.2.当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a||b|.3.a与b的夹角θ为锐角,则有a·b>0,反之不成立(θ为0时不成立);a与b的夹角为钝角,则有a·b<0,反之不成立(θ为π时不成立).【考点自诊】1.判断下列结论是否正确,正确的画“”,错误的画“×”.(1)一个非零向量在另一个非零向量

等比数列及其前n项和第三节返回1．等比数列的有关概念(1)定义：如果一个数列从第2项起，每一项与它的前一项的比等于同一常数(不为零)，那么这个数列就叫做等比数列．这个常数叫做等比数列的公比，通常用字母q表示，定义的表达式为an＋1an＝q.(2)等比中项：如果a，G，b成等比数列，那么G叫做a与b的等比中项．即G是a与b的等比中项⇔a，G，b成等比数列⇒G2＝ab.只有当两个数同号且不为0时，才有等比中项，且等比中项有两个.返回2．等比数列的有关公式(1)通项公式：an＝a1qn－1.(2)前n项和公式：Sn＝na1，q＝1，a1(1－qn)1－q＝a1－anq1－q，q≠1.①已知a1，q，n，an，Sn中的任意三个，即可求得其余两个，这体现了方程思想.②在等比数列求和时，要注意q＝1和q≠1的讨论.返回3．等比数列与指数型函数的关系当q>0且q≠1时，an＝a1q·qn可以看成函数y＝cqx，其是一个不为0的常数与指数函数的乘积，因此数列{an}各项所对应的点都在函数y＝cqx的图象上；对于非常数列的等比数列{an}的前n项和Sn＝a1(1－qn)1－q＝－a11－qqn＋a11－q，若设a＝a11－q，则Sn＝－aqn＋a(a≠0，q≠0，q≠1)．由此可知，数列{Sn}的图象是函数y＝－aqx＋a图象上一系列孤立的点．对于常数列的等比数列，即q＝1时，因为a1≠0，所以Sn＝na1.由此可知，数列{Sn}的图象是函数y＝a1x图象上一系列孤立的点．返回二、常用结论汇总——规律多一点返回设数列{an}是等比数列，Sn是其前n项和．(1)通项公式的推广：an＝am·qn－m(n，m∈N*)．(2)若m＋n＝p＋q，则aman＝apaq；若2s＝p＋r，则apar＝a2s，其中m，n，p，q，s，r∈N*.(3)ak，ak＋m，ak＋2m，…仍是等比数列，公比为qm(k，m∈N*)．(4)若数列{an}，{bn}是两个项数相同的等比数列，则数列{ban}，{pan·qbn}和panqbn也是等比数列．(5)若数列{an}的项数为2n，则S偶S奇＝q；若项数为2n＋1，则S奇－a1S偶＝q.返回(一)判一判(对的打“√”，错的打“×”)(1)满足an＋1＝qan(n∈N*，q为常数)的数列{an}为等比数列.()(2)三个数a，b，c成等比数列

变量间的相关关系与统计案例第三节课前自修区基础相对薄弱，一轮复习更需重视基础知识的强化和落实课堂讲练区考点不宜整合太大，挖掘过深否则会挫伤学习的积极性课时跟踪检测返回(1)常见的两变量之间的关系有两类：一类是函数关系，另一类是相关关系；与函数关系不同，相关关系是一种非确定性关系．1．变量间的相关关系(2)从散点图上看，点散布在从左下角到右上角的区域内，两个变量的这种相关关系称为；点散布在左上角到右下角的区域内，两个变量的这种相关关系为．正相关负相关2．两个变量的线性相关(1)从散点图上看，如果这些点从整体上看大致分布在通过散点图中心的一条直线附近，称两个变量之间具有线性相关关系，这条直线叫做回归直线．体现的不一定是因果关系.返回(2)回归方程为y^＝b^x＋a^，其中b^＝i＝1n(xi－x)(yi－y)i＝1n(xi－x)2＝i＝1nxiyi－nxyi＝1nx2i－nx2，a^＝y－b^x.回归直线y^＝b^x＋a^必过样本点的中心(x，y)，这个结论既是检验所求回归直线方程是否准确的依据，也是求参数的一个依据.(3)通过求Q＝i＝1n(yi－bxi－a)2的最小值而得到回归直线的方法，即使得样本数据的点到回归直线的距离的平方和最小，这一方法叫做最小二乘法．返回(4)相关系数：当r＞0时，表明两个变量；当r＜0时，表明两个变量．r的绝对值越接近于1，表明两个变量的线性相关性．r的绝对值越接近于0，表明两个变量之间几乎不存在线性相关关系．通常|r|大于0.75时，认为两个变量有很强的线性相关性．正相关负相关越强返回3．独立性检验(1)2×2列联表设X，Y为两个变量，它们的取值分别为{x1，x2}和{y1，y2}，其样本频数列联表(2×2列联表)如下：y1y2总计x1aba＋bx2cdc＋d总计a＋cb＋da＋b＋c＋d(2)独立性检验利用随机变量K2(也可表示为χ2)的观测值k＝n(ad－bc)2(a＋b)(c＋d)(a＋c)(b＋d)(其中n＝a＋b＋c＋d为样本容量)来判断“两个变量有关系”的方法称为独立性检验．独立性检验是对两个变量有关系的可信程度的判断，而不是对其是否有关系的判断．返回(1)求解回归方程的关键是确定回归系数a^，b^，应充分利用回归直线过样本中心点(x，y)．(2)根据K2的值可以判断两个分类变量有关的可信程度，若K2越大，则两分类

大一轮复习讲义高考专题突破四高考中的数列问题第七章数列与数学归纳法NEIRONGSUOYIN内容索引题型分类深度剖析课时作业题型分类深度剖析1PARTONE题型一等差数列、等比数列的基本问题师生共研例1(2018·浙江杭州地区四校联考)已知数列{an}满足a1＝1,1a2n＋4＝1an＋1，记Sn＝a21＋a22＋…＋a2n，若S2n＋1－Sn≤t30对任意的n∈N*恒成立.(1)求数列{a2n}的通项公式；解由题意得1a2n＋1－1a2n＝4，则1a2n是以1为首项，4为公差的等差数列，则1a2n＝1＋(n－1)×4＝4n－3，则a2n＝14n－3.解不妨设bn＝S2n＋1－Sn＝a2n＋1＋a2n＋2＋…＋a22n＋1，考虑到bn－bn＋1＝a2n＋1＋a2n＋2＋…＋a22n＋1－(a2n＋2＋a2n＋3＋…＋a22n＋2＋a22n＋3)＝a2n＋1－a22n＋2－a22n＋3(2)求正整数t的最小值.＝14n＋1－18n＋5－18n＋9＝18n＋2－18n＋5＋18n＋2－18n＋9>0，则bn的最大值为b1＝S3－S1＝a22＋a23＝15＋19＝1445≤t30，∴t≥283，则tmin＝10.等差数列、等比数列综合问题的解题策略(1)分析已知条件和求解目标，为最终解决问题设置中间问题，例如求和需要先求出通项、求通项需要先求出首项和公差(公比)等，确定解题的顺序.(2)注意细节：在等差数列与等比数列综合问题中，如果等比数列的公比不能确定，则要看其是否有等于1的可能，在数列的通项问题中第一项和后面的项能否用同一个公式表示等，这些细节对解题的影响也是巨大的.思维升华解设数列{an}的公差为d，依题意可得2＋2＋d＝3q，2＋d＝q2，解得d＝－1，q＝1(舍去)或d＝2，q＝2.跟踪训练1(2018·浙江名校联盟联考)已知等差数列{an}的前n项和为Sn，等比数列{bn}的公比是q(q≠1)，且满足：a1＝2，b1＝1，S2＝3b2，a2＝b3.(1)求an与bn；即λ>12×23n在n∈N*时成立，只需λ>12×23nmax.(2)设cn＝2bn－λ，若数列{cn}是递减数列，求实数λ的取值范围.23na解由(1)可知cn＝2n－λ·3n，若{cn}是递减数列

立体几何(必修2)第八章第一节空间几何体的结构、三视图和直观图高考概览：1.认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构；2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，能识别上述的三视图所表示的立体模型，会用斜二测画法画出它们的直观图；3.会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式．主干知识梳理Z主干梳理精要归纳[知识梳理]1．多面体的结构特征2．旋转体的形成3.空间几何体的三视图(1)三视图的名称几何体的三视图包括：．(2)三视图的画法①在画三视图时，重叠的线只画一条，挡住的线要画成虚线．②三视图的正视图、侧视图、俯视图分别是从几何体的方、方、方观察到的几何体的正投影图．正视图、侧视图、俯视图正前正左正上4．空间几何体的直观图空间几何体的直观图常用来画，其规则是：(1)原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴，y′轴的夹角为，z′轴与x′轴和y′轴所在平面．(2)原图形中平行于坐标轴的线段，直观图中仍；平行于x轴和z轴的线段在直观图中保持原长度；平行于y轴的线段在直观图中．斜二测画法45°或135°垂直平行于坐标轴不变长度变为原来的一半[辨识巧记]1．三类特殊多面体(1)直棱柱：侧棱与底面垂直的棱柱称为直棱柱．(2)正棱柱：正棱柱是侧棱都垂直于底面，且底面是正多边形的棱柱．(3)正棱锥：底面是正多边形，且顶点在底面的投影为底面中心的棱锥为正棱锥．2．一个结论利用斜二测画法画出的水平放置的平面图形的直观图的面积是原来图形的24倍．3．旋转体三视图的常见结论(1)球的三视图都是半径相等的圆．(2)水平放置的圆锥的正视图和侧视图均为全等的等腰三角形．(3)水平放置的圆台的正视图和侧视图均为全等的等腰梯形．(4)水平放置的圆柱的正视图和侧视图均为全等的矩形．[双基自测]1．判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)有两个面平行，其余各面都是平行四边形的几何体是棱柱．()(2)有一个面是多边形，其余各面都是三角形的几何体是棱锥．()(3)用斜二测画法画水平放置的∠A时，若∠A的两边分别平行于x轴和y轴，且∠A＝90°，则在直观图中，∠A＝45°.()(4)正方体、球、圆锥各自的三视图中，三视图均相同．()[答案](1)×(2)

不等式、推理与证明(必修5、选修1－2)第七章2020版高考文科数学一轮复习课件第一节不等式的性质、一元二次不等式高考概览：1.掌握不等式的性质及应用；2.会从实际情境中抽象出一元二次不等式模型；3.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的关系；4.会解一元二次不等式．主干知识梳理Z主干梳理精要归纳[知识梳理]1．两个实数比较大小的方法(1)作差法a－b>0⇔a>b，a－b＝0⇔a＝b(a，b∈R)，a－b<0⇔a<b.(2)作商法ab>1⇔a>b(a∈R，b>0)，ab＝1⇔a＝b(a∈R，b>0)，ab<1⇔a<b(a∈R，b>0).2．不等式的基本性质3．不等式的一些常用性质(1)倒数的性质①a>b，ab>0⇒1a1b.②a<0<b⇒1a1b.(2)有关分数的性质若a>b>0，m>0，则：①ba<b＋ma＋m；ba>b－ma－m(b－m>0)．②ab>a＋mb＋m；ab<a－mb－m(b－m>0)．<<4．三个二次之间的关系5.简单分式不等式的解法x－ax－b>0等价于(x－a)(x－b)>0；x－ax－b<0等价于(x－a)(x－b)<0；x－ax－b≥0等价于(x－a)(x－b)≥0，x－b≠0；x－ax－b≤0等价于(x－a)(x－b)≤0，x－b≠0.[辨识巧记]1．倒数性质的几个必备结论(1)a>b，ab>0⇒1a<1b.(2)a<0<b⇒1a<1b.(3)a>b>0,0<c<d⇒ac>bd.(4)0<a<x<b或a<x<b<0⇒1b<1x<1a.2．一元二次不等式的解法技巧求不等式ax2＋bx＋c>0(a>0)的解集，先求出对应方程ax2＋bx＋c＝0(a>0)的根，再根据口诀：大于取两边，小于取中间求解集．[双基自测]1．判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)若ab>1，则a>b.()(2)若ab>0，则a>b⇔1a<1b.()(3)若不等式ax2＋bx＋c>0的解集是(－∞，x1)∪(x2，＋∞)，则方程ax2＋bx＋c＝0的两个根是x1和x2.()(4)一元二次不等式ax2＋bx＋c≤0在R上恒成立的条件是a<0且Δ＝b2－4ac≤0.()[答案](1)×(2)√(3)√(4)√2．(2018·唐山模拟)若a，b为实数，且a<b<0，则下列不等式正确的

第9章算法初步、统计与统计第一节算法与程序框图[考纲传真]1.了解算法的含义，了解算法的思想.2.理解图的三种基本逻辑结构：顺序结构、条件结构、循环结构.3.了基本算法语句——输入语句、输出语句、赋值语句、条件语句语句的含义．栏目导航课堂题型全突破真题自主验效果课前知识全通关课后限时集训01020304课前知识全通关1．算法(1)算法通常是指按照__________解决某一类问题的______的步骤．(2)应用：算法通常可以编成计算机______，让计算机执决问题．2．程序框图程序框图又称流程图，是一种用________、流程线及____来表示算法的图形．一定规则明有限程序程序框文字答案2．三种基本逻辑结构及相应语句名称示意图相应语句顺序结构①输入语句：INPUT“提示内容”；变量②输出语句：PRINT“提示内容”；表达式③赋值语句：变量＝表达式IF条件THEN语句体ENDIF条件结构IF条件THEN语句体1ELSE语句体2ENDIF直到型循环结构DO循环体LOOPUNTIL条件循环结构当型循环结构WHILE条件循环体WEND[常用结论]1．注意区分处理框与输入框，处理框主要是赋值、计算入框只是表示一个算法输入的信息．2．循环结构中必有条件结构，其作用是控制循环进程，入“死循环”，是循环结构必不可少的一部分．3．注意区分当型循环与直到型循环．直到型循环是“先后判断，条件满足时终止循环”，而当型循环则是“先判断，后条件满足时执行循环”．两者的判断框内的条件表述在解决同时是不同的，它们恰好相反．[基础自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，打“×”)(1)算法只能解决一个问题，不能重复使用．(2)程序框图中的图形符号可以由个人来确定．(3)输入框只能紧接开始框，输出框只能紧接结束框．(4)条件结构的出口有两个，但在执行时，只有一个出口的．()(5)5＝x是赋值语句．(6)输入语句可以同时给多个变量赋值．[答案](1)×(2)×(3)×(4)√(5)×(6)√2．(教材改编)执行如图所示的程序框图，则输出S的值为A．－32B．32C．－12D．12D[按照程序框图依次循环运算，当k＝5时，停止循环，当k＝5时，S＝sin5π6＝12.]解析答案3．(教材改编)根据给出的程序框图，计算f(－1)＋f(2)＝A．0B．1C．2D．4A[f(－1)＝4×(－

第8节函数的应用(二)【教材回扣】1．函数的零点(1)函数的零点的概念对于函数y＝f(x)，我们把使________的实数x叫做函数y＝f(x)的零点．(2)方程、函数、图象之间的关系方程f(x)＝0有实数解⇔函数y＝f(x)________⇔函数y＝f(x)的图象与x轴有公共点．(3)函数的零点的本质是方程f(x)＝0的实数解，因此，函数的零点不是点，而是一个实数．例如函数f(x)＝x＋1，当f(x)＝x＋1＝0时，仅有一个实数解x＝－1，所以函数f(x)＝x＋1有一个零点－1.f(x)＝0有零点2．函数零点存在定理如果函数y＝f(x)在区间[a，b]上的图象是一条________的曲线，且有________，那么，函数y＝f(x)在区间(a，b)内至少有一个零点，即存在c∈(a，b)，使得________，这个c也就是方程f(x)＝0的解．连续不断f(a)·f(b)<0f(c)＝03．二次函数y＝ax2＋bx＋c(a>0)的图象与零点的关系Δ>0Δ＝0Δ<0二次函数y＝ax2＋bx＋c(a>0)的图象与x轴的交点________________无交点零点个数210(x1,0)，(x2,0)(x1,0)4.常见的函数模型(1)一次函数模型y＝kx＋b(k，b为常数，k≠0)(2)二次函数模型y＝ax2＋bx＋c(a，b，c为常数，a≠0)(3)指数型函数模型y＝bax＋c(a，b，c为常数，b≠0，a>0且a≠1)(4)对数型函数模型y＝mlogax＋n(m，a，n为常数，m≠0，a>0且a≠1)常见函数模型(5)幂函数型模型y＝axα＋b(a，b为常数，a≠0)【教材提炼】一、教材改编1．[必修一·P155习题4.5T4改编]函数f(x)＝lnx－2x的零点所在的大致区间是()A．(1,2)B．(2,3)C．(1e，1)和(3,4)D．(4，＋∞)答案：B解析：∵f(2)＝ln2－1<0，f(3)＝ln3－23>0，且函数f(x)的图象在(0，＋∞)上连续不断，f(x)为增函数，∴f(x)的零点在区间(2,3)内．2．[必修一·P156习题4.5T13改编]若函数f(x)＝24ax2＋4x－1在区间(－1,1)内恰有一个零点，则实数a的取值范围是________．答案：{0，－16}∪(－18，524)解析：(1)当a＝0时，f(x)＝4x－1.令f(x)＝0，

第6讲利用导数研究函数的零点问题第三章导数及其应用第三章导数及其应用设函数f(x)＝lnx＋mx，m∈R.(1)当m＝e(e为自然对数的底数)时，求f(x)的极小值；(2)讨论函数g(x)＝f′(x)－x3零点的个数．判断函数零点的个数(师生共研)第三章导数及其应用【解】(1)由题设，当m＝e时，f(x)＝lnx＋ex，定义域为(0，＋∞)，则f′(x)＝x－ex2，由f′(x)＝0，得x＝e.所以当x∈(0，e)时，f′(x)<0，f(x)在(0，e)上单调递减，当x∈(e，＋∞)时，f′(x)>0，f(x)在(e，＋∞)上单调递增，所以当x＝e时，f(x)取得极小值f(e)＝lne＋ee＝2，所以f(x)的极小值为2.第三章导数及其应用(2)由题设g(x)＝f′(x)－x3＝1x－mx2－x3(x>0)，令g(x)＝0，得m＝－13x3＋x(x>0)．设φ(x)＝－13x3＋x(x>0)，则φ′(x)＝－x2＋1＝－(x－1)(x＋1)，当x∈(0，1)时，φ′(x)>0，φ(x)在(0，1)上单调递增；当x∈(1，＋∞)时，φ′(x)<0，φ(x)在(1，＋∞)上单调递减．所以x＝1是φ(x)的唯一极值点，且是极大值点，第三章导数及其应用因此x＝1也是φ(x)的最大值点．所以φ(x)的最大值为φ(1)＝23.又φ(0)＝0，结合y＝φ(x)的图象(如图)，可知①当m>23时，函数g(x)无零点；②当m＝23时，函数g(x)有且只有一个零点；第三章导数及其应用③当0<m<23时，函数g(x)有两个零点；④当m≤0时，函数g(x)有且只有一个零点．综上所述，当m>23时，函数g(x)无零点；当m＝23或m≤0时，函数g(x)有且只有一个零点；当0<m<23时，函数g(x)有两个零点．第三章导数及其应用函数的零点个数也就是函数图象与x轴交点的个数，所以可以借助函数图象的特征迅速求解函数的零点个数问题．对于含参函数的零点个数，一般可从两个方面讨论：一是利用导数研究函数的单调性和极值，作出函数的大致图象，根据极大值和极小值的符号确定函数零点的个数；二是分离参数，将问题转化为求y＝a和y＝f(x)的图象的交点个数问题求解．第三章导数及其应用(2019·长春市质量监测(二))已知函数f(x)＝ex＋bx－1(b∈R)．(1)讨论f(x)的单调性；(2)若方程f(x)＝lnx

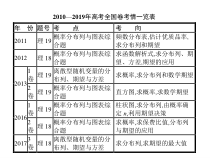
2010—2019年高考全国卷考情一览表年份题号考点考向2011理19概率分布列与图表综合题频数分布表,估计优质品率,求分布列和期望2012理18概率分布列与图表综合题求函数解析式,求分布列、期望、方差,期望的应用20131卷理19离散型随机变量的分布列、期望与方差求概率,求分布列和数学期望2卷理19概率分布列与图表综合题直方图,求概率,求数学期望20161卷理19概率分布列与图表综合题柱状图,求分布列,由概率确定n,利用期望决策2卷理18概率分布列与图表综合题求概率,求保费比值,分布列与期望的应用20173卷理18离散型随机变量的分布列、期望与方差求分布列,求期望的最大值年份题号考点考向20181卷理20离散型随机变量的分布列、期望与方差求期望,并依据期望进行决策3卷理8离散型随机变量的分布列、期望与方差独立重复试验,已知方差求概率20191卷理21离散型随机变量的分布列、期望与方差求分布列及解释方案的合理性考情分析与预测1.高考考查频率不高,高考主要考查三个方面:(1)求离散型随机变量的分布列,期望,方差;(2)分布列、期望与统计图表综合应用;(3)利用分布列、期望、方差进行决策或分析.此类试题阅读量大,知识综合.2.2020年高考将保持稳定.考点116考点117考点116离散型随机变量的分布列、期望与方差1.(2018·浙江,7,4分,难度★★)设0<p<1,随机变量ξ的分布列是ξ012P1-p212p2则当p在(0,1)内增大时,(D)A.D(ξ)减小B.D(ξ)增大C.D(ξ)先减小后增大D.D(ξ)先增大后减小解析由题意可知,E(ξ)=0×1-𝑝2+1×12+2×𝑝2=12+p,D(ξ)=0-12-𝑝2×1-𝑝2+1-12-𝑝2×12+2-12-𝑝2×𝑝2=12-2𝑝2+2𝑝+12=-𝑝2-𝑝+14-12=-𝑝-122+12,p∈(0,1).故当p在(0,1)内增大时,D(ξ)先增大后减小.考点116考点1172.(2019·全国1,理21,12分,难度★★)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就

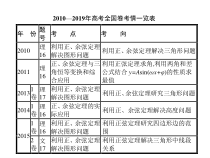
2010—2019年高考全国卷考情一览表年份题号考点考向2010理16利用正、余弦定理解决图形问题利用正、余弦定理解决三角形问题2011理16正、余弦定理与三角恒等变换和综合应用利用正弦定理求角,利用两角和差公式结合y=Asin(ωx+φ)的性质求最值20131卷理17利用正、余弦定理解决图形问题利用正、余弦定理研究三角形问题20141卷理16正、余弦定理的实际应用利用正、余弦定理解决高度问题20151卷理16利用正、余弦定理解决图形问题利用正弦定理研究四边形边的范围2卷文17利用正、余弦定理解决图形问题利用正弦定理解决三角形中线段关系年份题号考点考向20171卷文11正、余弦定理与三角恒等变换的综合应用根据两角和差公式结合正弦定理求角20191卷文11正、余弦定理与三角恒等变换的综合应用正、余弦定理的综合应用3卷理18文18正、余弦定理与三角恒等变换的综合应用求角的度数及三角形面积的取值范围考情分析与预测1.高考常考内容,属中档题,高考对本节的考查主要有三个方面:(1)正余弦定理与三角恒等变换的综合应用:解三角形、边角统一思想与三角恒等变换的综合应用求角的三角函数值或者范围;(2)利用正余弦定理解决图形问题:分析给出的图形,将已知条件先集中到某个三角形中,解三角形,再依次解其他三角形,直至求出结果;(3)正余弦定理的实际应用:建立三角函数模型,利用解三角形公式求出边或角.2.2020年高考对本节的考查不会有大的变化,仍是考查正余弦定理与三角恒等变换的综合应用以及解决图形中的边角问题.考点54考点55考点56考点54正、余弦定理与三角恒等变换的综合应用1.(2019·全国1,文11,5分,难度★★)△ABC的内角A,B,C的对边分别为a,b,c.已知asinA-bsinB=4csinC,cosA=-14,则𝑏𝑐=(A)A.6B.5C.4D.3解析由已知及正弦定理,得a2-b2=4c2,由余弦定理的推论,得-14=cosA=𝑏2+𝑐2-𝑎22𝑏𝑐,∴𝑐2-4𝑐22𝑏𝑐=-14,∴-3𝑐2𝑏=-14,∴𝑏𝑐=32×4=6,故选A.考点54考点55考点562.(2017·全国1,文11,5分,难度★★)△ABC的内角A,B,C的对边分别为a,b,c.已知sinB+sinA(sinC-cosC)=0,a=2,c=2,则C=(B)A.π12B.π

第四节函数y＝Asin(ωx＋φ)的图象及三角函数模型的简单应用教材回顾考点突破栏目导航最新考纲考情考向分析1.了解函数y＝Asin(ωx＋φ)的物理意义；能画出y＝Asin(ωx＋φ)的图象．2．了解参数A，ω，φ对函数图象变化的影响．3．会用三角函数解决一些简单实际问题，体会三角函数是描述周期变化现象的重要函数模型.以考查函数y＝Asin(ωx＋φ)的图象的五点法画图、图象之间的平移伸缩变换、由图象求函数解析式以及利用正弦型函数解决实际问题为主，常与三角函数的性质、三角恒等变换结合起来进行综合考查，加强数形结合思想的应用意识．题型为选择题和填空题，中档难度.[基础梳理]1．五点法画函数y＝Asin(ωx＋φ)的图象(1)列表：(2)描点：，，，，.(3)连线：把这5个点用光滑曲线顺次连接，就得到y＝Asin(ωx＋φ)在区间长度为一个周期内的图象．－φω，0π2ω－φω，Aπω－φω，03π2ω－φω，－A2πω－φω，02．函数y＝sinx的图象经变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种途径3．y＝Asin(ωx＋φ)的物理意义4.三角函数的零点、不等式问题(1)把函数表达式转化为正弦型函数形式y＝Asin(ωx＋φ)＋B(A>0，ω>0)．(2)画出长度为一个周期的区间上的函数图象．(3)利用图象解决有关三角函数的方程、不等式问题．[三基自测]1．(必修4·习题1.5A组改编)为了得到函数y＝sin2x－π3的图象，只需把函数y＝sin2x＋π6的图象()A．向左平移π4个单位长度B．向右平移π4个单位长度C．向左平移π2个单位长度D．向右平移π2个单位长度答案：B2．(必修4·习题1.5A组改编)已知简谐运动f(x)＝2sinπ3x＋φ|φ|<π2的图象经过点(0,1)，则该简谐运动的最小正周期T和初相φ分别为()A．T＝6，φ＝π6B．T＝6，φ＝π3C．T＝6π，φ＝π6D．T＝6π，φ＝π3答案：A3．(必修4·习题1.5A组改编)电流i(单位：A)随时间t(单位：s)变化的函数关系是i＝5sin100πt＋π3，t∈[0，＋∞)，则电流i变化的初相、周期分别是．答案：π3，1504．(必修4·习题1.5例题改

第2章函数、导数及其应用第1讲函数及其表示板块一知识梳理·自主学习[必备知识]考点1函数与映射的概念考点2函数的三要素函数由定义域、和值域三个要素构成，对函数y＝f(x)，x∈A，其中(1)定义域：的取值构成的集合；(2)值域：函数值的集合考点3函数的表示法表示函数的常用方法有：对应关系自变量x{f(x)|x∈A}．解析法、列表法、图象法．考点4分段函数若函数在定义域的不同子集上，因不同而分别用几个不同的式子来表示，这种函数称为分段函数．对应关系[必会结论]1．映射：(1)映射是函数的推广，函数是特殊的映射，A，B为非空数集的映射就是函数；(2)映射的两个特征：第一，在A中取元素的任意性；第二，在B中对应元素的唯一性；(3)映射问题允许多对一，但不允许一对多．2．判断两个函数相等的依据是两个函数的定义域和对应关系完全一致．3．分段函数的定义域等于各段函数的定义域的并集，其值域等于各段函数的值域的并集，分段函数虽由几个部分组成，但它表示的是一个函数．4．与x轴垂直的直线和一个函数的图象至多有1个交点．[双基夯实]一、疑难辨析判断下列结论的正误．(正确的打“√”，错误的打“×”)1．若A＝R，B＝{x|x>0}，f：x→y＝|x|，其对应是从A到B的映射．()2．函数f(x)＝x2－2x与g(t)＝t2－2t是同一函数．()×√3．若两个函数的定义域与值域相同，则这两个函数相等．()4．若f(x)＝|x－1|－|x|，则ff12＝0.()5．分段函数是由两个或几个函数组成的．()×××二、小题快练1．下列图象可以表示以M＝{x|0≤x≤1}为定义域，以N＝{x|0≤x≤1}为值域的函数的是()解析A选项中的值域不对，B选项中的定义域错误，D选项不是函数的图象，由函数的定义可知选项C正确．2．[2017·济宁模拟]已知函数f(x)满足f(2x)＝2f(x)，且当1≤x<2时，f(x)＝x2，则f(3)＝()A.98B.94C.92D．9解析∵f(2x)＝2f(x)，且当1≤x<2时，f(x)＝x2，∴f(3)＝2f32＝2×322＝92.3．[2016·江苏高考]函数y＝3－2x－x2的定义域是________．[－3,1]解析若函数有意义，则3－2x－x2≥0，即x2＋2x－3≤0，解得－3≤x≤1.4．[

2020年高考一轮复习函数模型及其应用2023年5月31日星期三最新考纲考情索引核心素养1.了解指数函数、对数函数以及幂函数的增长特征，知道直线上升、指数增长、对数增长等不同函数类型增长的含义．2.了解函数模型(如指数函数、对数函数、幂函数、分段函数等普遍使用的函数模型)在社会生活的广泛应用.2018·浙江卷，T112018·天津卷，T142017·全国卷Ⅲ，T32016·全国卷Ⅲ，T41.数学建模2.直观想象3.数学运算1．指数、对数、幂函数模型性质比较函数性质y＝ax(a＞1)y＝logax(a＞1)y＝xn(n＞0)在(0，＋∞)上的增减性单调_____单调_____单调递增增长速度越来越快越来越慢相对平稳递增递增图象的变化随x的增大逐渐表现为与____平行随x的增大逐渐表现为与______平行随n值变化而各有不同值的比较存在一个x0，当x＞x0时，有logax＜xn＜axy轴x轴2.几种常见的函数模型函数模型函数解析式一次函数模型f(x)＝ax＋b(a，b为常数，a≠0)二次函数模型f(x)＝ax2＋bx＋c(a，b，c为常数，a≠0)与指数函数相关模型f(x)＝bax＋c(a，b，c为常数，a>0且a≠1，b≠0)与对数函数相关模型f(x)＝blogax＋c(a，b，c为常数，a>0且a≠1，b≠0)与幂函数相关模型f(x)＝axn＋b(a，b，n为常数，a≠0)3.解函数应用问题的步骤(1)审题：弄清题意，分清条件和结论，理顺数量关系，初步选择数学模型.(2)建模：将自然语言转化为数学语言，将文字语言转化为符号语言，利用数学知识，建立相应的数学模型．(3)解模：求解数学模型，得出数学结论．(4)还原：将数学问题还原为实际问题．以上过程用框图表示如下：1．“直线上升”是匀速增长，其增长量固定不变；“指数增长”先慢后快，其增长量成倍增加，常用“指数爆炸”来形容；“对数增长”先快后慢，其增长速度缓慢．2．充分理解题意，并熟练掌握几种常见函数的图象和性质是解题的关键．3．易忽视实际问题中自变量的取值范围，需合理确定函数的定义域，必须验证数学结果对实际问题的合理性．1．概念思辨判断下列说法的正误(正确的打“√”，错误的打“×”)．(1)某种商品进价为每件100元，按进价增加10%出售，后因库存积压降价，若按九折出售，则每件还能获利.()(2)函数y＝2x的函数值比

2020年高考一轮复习函数y＝Asin(ωx＋φ)的图象及应用2023年5月31日星期三最新考纲考情索引核心素养1.了解函数y＝Asin(ωx＋φ)的物理意义；能画出函数y＝Asin(ωx＋φ)的图象，了解参数A，ω，φ对函数图象变化的影响．2.了解三角函数是描述周期变化现象的重要函数模型，会用三角函数解决一些简单的实际问题.2018·天津卷，T62016·全国卷Ⅰ，T62016·全国卷Ⅲ，T141.数学运算2.直观想象1．用五点法画y＝Asin(ωx＋φ)一个周期内的简图用五点法画y＝Asin(ωx＋φ)一个周期内的简图时，要找五个关键点，如下表所示．x___－φω＋π2ω___3π2ω－φω___ωx＋φ0___π___2πy＝Asin(ωx＋φ)0A0－A0－φωπ－φω2π－φωπ23π22.函数y＝Asin(ωx＋φ)中各量的物理意义简谐振动振幅周期频率相位初相y＝Asin(ωx＋φ)(A>0，ω>0)x∈[0，＋∞]A______f＝1T_____φT＝2πωωx＋φ3.函数y＝sinx的图象经变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种途径1．由y＝sinωx到y＝sin(ωx＋φ)(ω>0，φ>0)的变换：向左平移φω个单位长度而非φ个单位长度．2．函数y＝Asin(ωx＋φ)的对称轴由ωx＋φ＝kπ＋π2，k∈Z确定；对称中心由ωx＋φ＝kπ，k∈Z确定其横坐标．1．概念思辨判断下列结论的正误(正确的打“√”，错误的打“×”)．(1)将函数y＝3sin2x的图象左移π4个单位长度后所得图象的解析式是y＝3sin2x＋π4.()(2)利用图象变换作图时“先平移，后伸缩”与“先伸缩，后平移”中平移的长度一致．()(3)函数y＝Acos(ωx＋φ)的最小正周期为T，那么函数图象的两个相邻对称中心之间的距离为T2.()(4)由图象求解析式时，振幅A的大小是由一个周期内图象中最高点的值与最低点的值确定的．()解析：(1)将函数y＝3sin2x的图象向左平移π4个单位长度后所得图象的解析式是y＝3cos2x.(2)“先平移，后伸缩”的平移单位长度为|φ|，而“先伸缩，后平移”的平移单位长度为φω.故当ω≠1时平移的长度不相等．答案：(1)×(2)×(3)√(4)√2．教材衍化(1)(人A必修4·P56T3改编)y＝2s

2020年高考一轮复习简单的逻辑联结词、全称量词与存在量词2023年5月31日星期三最新考纲考情索引核心素养1.了解逻辑联结词“或”“且”“非”的含义．2.理解全称量词与存在量词的意义．3.能正确地对含有一个量词的命题进行否定.2017·山东卷，T51.逻辑推理2.数学运算1．简单的逻辑联结词(1)命题中的“___”“___”“___”叫做逻辑联结词．(2)命题p∧q，p∨q，¬p的真假判断．且或非pqp∧qp∨q¬p真真___真___真假______假假真假______假假___假___真假假真真真假真2.全称量词与存在量词(1)全称量词：短语“所有的”“任意一个”等在逻辑中通常叫做全称量词，用符号“___”表示．(2)存在量词：短语“存在一个”“至少有一个”等在逻辑中通常叫做存在量词，用符号“___”表示．∀∃3．全称命题和特称命题名称形式全称命题特称命题结构对M中的任意一个x，有p(x)成立存在M中的一个x0，使p(x0)成立简记____________________________否定∃x0∈M，¬p(x0)_______，¬p(x)∀x∈M，p(x)∃x0∈M，p(x0)∀x∈M1．含有逻辑联结词的命题真假判断口诀：p∨q→见真即真，p∧q→见假即假，p与¬p→真假相反．2．含有一个量词的命题的否定规律是“改量词，否结论”．3．“p∨q”的否定是“(¬p)∧(¬q)”，“p∧q”的否定是“(¬p)∨(¬q)”．1．概念思辨判断下列结论的正误(正确的打“√”，错误的打“×”)．(1)命题“5>6或5>2”是假命题.()(2)命题¬(p∧q)是假命题，则命题p，q中至少有一个是真命题．()(3)“长方形的对角线相等”是特称命题．()(4)∃x0∈M，p(x0)与∀x∈M，¬p(x)的真假性相反．()解析：(1)错误．命题p∨q中，p，q有一真则真．(2)错误．p∧q是真命题，则p，q都是真命题．(3)错误．命题“长方形的对角线相等”是全称命题．答案：(1)×(2)×(3)×(4)√2．教材衍化(1)(人A选修1－1·P26A组T3改编)命题“∀x∈R，x2＋x≥0”的否定是()A．∃x0∈R，x20＋x0≤0B．∃x0∈R，x20＋x0<0C．∀x∈R，x2＋x≤0D．∀x∈R，x2＋x<0解析：由全称命题的否定是特称命题知命题B正确．答案：B(2)(人A选

2020年高考一轮复习正弦定理和余弦定理2023年5月31日星期三最新考纲考情索引核心素养掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.2018·全国卷Ⅰ，T162018·全国卷Ⅱ，T72018·全国卷Ⅲ，T112017·全国卷Ⅰ，T112017·全国卷Ⅱ，T162017·全国卷Ⅲ，T152016·全国卷Ⅰ，T42016·全国卷Ⅱ，T151.数学运算2.逻辑推理1．正、余弦定理在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则定理正弦定理余弦定理公式____________________＝2Ra2＝b2＋c2－2bccosA；b2＝_______________；c2＝_______________asinA＝bsinB＝csinCc2＋a2－2cacosBa2＋b2－2abcosC常见变形(1)a＝2RsinA，b＝________，c＝________；(2)sinA＝a2R，sinB＝b2R，sinC＝c2R(3)a∶b∶c＝__________________；(4)asinB＝bsinA，bsinC＝csinB，asinC＝csinAcosA＝________；cosB＝________；cosC＝________2RsinB2RsinCsinA∶sinB∶sinCb2＋c2－a22bcc2＋a2－b22caa2＋b2－c22ab2.S△ABC＝12absinC＝12bcsinA＝12acsinB＝abc4R＝12(a＋b＋c)·r(r是三角形内切圆的半径)，并可由此计算R，r.3．在△ABC中，已知a，b和A时，解的情况如下：项目A为锐角A为钝角或直角图形关系式a＝bsinAbsinA＜a＜ba≥ba＞ba≤b解的个数____________________________一解两解一解一解无解1．三角形中的三角函数关系．(1)sin(A＋B)＝sinC；(2)cos(A＋B)＝－cosC；(3)sinA＋B2＝cosC2；(4)cosA＋B2＝sinC2.2．三角形中的射影定理．在△ABC中，a＝bcosC＋ccosB；b＝acosC＋ccosA；c＝bcosA＋acosB.3．△ABC中，∠A>∠B⇔a>b⇔sinA>sinB⇔cosA<cosB.1．概念思辨判断下列结论的正误(正确的打“√”，错误的打“×”