【文档说明】2020高考数学大一轮复习指导课件第十一章概率统计与统计案例离散型随机变量的分布列期望与方差.ppt，共(58)页，1.833 MB，由小橙橙上传

转载请保留链接：https://www.ichengzhen.cn/view-256673.html

以下为本文档部分文字说明：

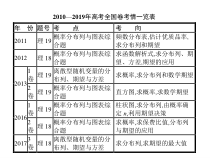
2010—2019年高考全国卷考情一览表年份题号考点考向2011理19概率分布列与图表综合题频数分布表,估计优质品率,求分布列和期望2012理18概率分布列与图表综合题求函数解析式,求分布列、期望、方差,期望的应用20131卷理19

离散型随机变量的分布列、期望与方差求概率,求分布列和数学期望2卷理19概率分布列与图表综合题直方图,求概率,求数学期望20161卷理19概率分布列与图表综合题柱状图,求分布列,由概率确定n,利用期望决策2卷理18概率

分布列与图表综合题求概率,求保费比值,分布列与期望的应用20173卷理18离散型随机变量的分布列、期望与方差求分布列,求期望的最大值年份题号考点考向20181卷理20离散型随机变量的分布列、期望与方差求期望,

并依据期望进行决策3卷理8离散型随机变量的分布列、期望与方差独立重复试验,已知方差求概率20191卷理21离散型随机变量的分布列、期望与方差求分布列及解释方案的合理性考情分析与预测1.高考考查频率不高,

高考主要考查三个方面:(1)求离散型随机变量的分布列,期望,方差;(2)分布列、期望与统计图表综合应用;(3)利用分布列、期望、方差进行决策或分析.此类试题阅读量大,知识综合.2.2020年高考将保持稳定.考点116考点117考点116离散型随机变量的分布列、期望与方差1

.(2018·浙江,7,4分,难度★★)设0<p<1,随机变量ξ的分布列是ξ012P1-p212p2则当p在(0,1)内增大时,(D)A.D(ξ)减小B.D(ξ)增大C.D(ξ)先减小后增大D.D(ξ)先增

大后减小解析由题意可知,E(ξ)=0×1-𝑝2+1×12+2×𝑝2=12+p,D(ξ)=0-12-𝑝2×1-𝑝2+1-12-𝑝2×12+2-12-𝑝2×𝑝2=12-2𝑝2+2𝑝+12=-𝑝2-𝑝+14-12=-𝑝-

122+12,p∈(0,1).故当p在(0,1)内增大时,D(ξ)先增大后减小.考点116考点1172.(2019·全国1,理21,12分,难度★★)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于

两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施

以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.考点116考点117(1)求X的分布列;(2)若甲药

、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c

=P(X=1).假设α=0.5,β=0.8.(ⅰ)证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;(ⅱ)求p4,并根据p4的值解释这种试验方案的合理性.考点116考点117解(1)X的所有可能取值为-1,0,1.P(X=-1)=(1-α

)β,P(X=0)=αβ+(1-α)(1-β),P(X=1)=α(1-β).所以X的分布列为X-101P(1-α)βαβ+(1-α)(1-β)α(1-β)(2)(ⅰ)由(1)得a=0.4,b=0.5,c=0.1.因此pi=0.4pi-1+0.5pi

+0.1pi+1,故0.1(pi+1-pi)=0.4(pi-pi-1),即pi+1-pi=4(pi-pi-1).又因为p1-p0=p1≠0,所以{pi+1-pi}(i=0,1,2,…,7)为公比为4,首项为p1的等比数列.考点116考点117(ⅱ)由(ⅰ)可得p8=p8-p7+

p7-p6+…+p1-p0+p0=(p8-p7)+(p7-p6)+…+(p1-p0)=48-13p1.由于p8=1,故p1=348-1,所以p4=(p4-p3)+(p3-p2)+(p2-p1)+(p1-p0)=44-13p1=

1257.p4表示最终认为甲药更有效的概率.由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,认为甲药更有效的概率为p4=1257≈0.0039,此时得出错误结论的概率非常小,说明这种试验方案合理.考点116

考点1173.(2018·全国1,理20,12分,难度★★)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验.设每件

产品为不合格品的概率都为p(0<p<1),且各件产品是否为不合格品相互独立.(1)记20件产品中恰有2件不合格品的概率为f(p),求f(p)的最大值点p0.(2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p0作为p的值.已知每件产品的检验费用为2元,若有不合格品进

入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.①若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X,求EX;②以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有

产品作检验?考点116考点117解(1)20件产品中恰有2件不合格品的概率为f(p)=C202p2(1-p)18.因此f'(p)=C202[2p(1-p)18-18p2(1-p)17]=2C202p(1-p)17(1

-10p).令f'(p)=0,得p=0.1.当p∈(0,0.1)时,f'(p)>0;当p∈(0.1,1)时,f'(p)<0.所以f(p)的最大值点为p0=0.1.(2)由(1)知,p=0.1.①令Y表示余下的1

80件产品中的不合格品件数,依题意知Y~B(180,0.1),X=20×2+25Y,即X=40+25Y.所以EX=E(40+25Y)=40+25EY=490.②如果对余下的产品作检验,则这一箱产品所需要的检验费为400元.由于EX>

400,故应该对余下的产品作检验.考点116考点1174.(2018·北京,理17,12分,难度★★)电影公司随机收集了电影的有关数据,经分类整理得到下表:电影类型第一类第二类第三类第四类第五类第六类电影部数14050300200800510好评率0.40.20.150.250.20.1好评率是

指:一类电影中获得好评的部数与该类电影的部数的比值.假设所有电影是否获得好评相互独立.(1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;(2)从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率;考点116考点117(3)假设每类电

影得到人们喜欢的概率与表格中该类电影的好评率相等.用“ξk=1”表示第k类电影得到人们喜欢,“ξk=0”表示第k类电影没有得到人们喜欢(k=1,2,3,4,5,6).写出方差Dξ1,Dξ2,Dξ3,Dξ4,Dξ5,Dξ6的大小关系.解(1)设“从电影公司收集的电影中随机选取1部,这部电影是获得好评

的第四类电影”为事件A,第四类电影中获得好评的电影为200×0.25=50(部).P(A)=50140+50+300+200+800+510=502000=0.025.(2)设“从第四类电影和第五类电

影中各随机选取1部,恰有1部获得好评”为事件B,P(B)=0.25×0.8+0.75×0.2=0.35.(3)由题意可知,定义随机变量如下:ξk=0,第𝑘类电影没有得到人们喜欢,1,第𝑘类电影得到人们喜欢,考点116考点117则ξk显然服从两点分布,则六类电影

的分布列及方差计算如下:第一类电影:ξ110P0.40.6Dξ1=0.4×0.6=0.24;第二类电影:ξ210P0.20.8Dξ2=0.2×0.8=0.16;第三类电影:ξ310P0.150.85Dξ3=0.15×0.85=0.1275;考点116考点117第四类电影:ξ

410P0.250.75Dξ4=0.25×0.75=0.1875;第五类电影:ξ510P0.20.8Dξ5=0.2×0.8=0.16;第六类电影:ξ610P0.10.9Dξ6=0.1×0.9=0.09;综上所述,Dξ1>Dξ4>Dξ2=Dξ5>Dξ3>Dξ6.考点116考点1175.(2

018·天津,理16,13分,难度★★)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?(2)若抽出的7人中有4人睡眠不足,3人睡

眠充足,现从这7人中随机抽取3人做进一步的身体检查.①用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;②设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.考点116考点117解(1)由已知,甲、乙、丙

三个部门的员工人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.(2)①随机变量X的所有可能取值为0,1,2,3.P(X=k)=C4𝑘·C

33-𝑘C73(k=0,1,2,3).所以,随机变量X的分布列为X0123P13512351835435随机变量X的数学期望E(X)=0×135+1×1235+2×1835+3×435=127.考点116考点117②设事件B为“抽取的3人中,睡眠充足的员工

有1人,睡眠不足的员工有2人”;事件C为“抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人”,则A=B∪C,且B与C互斥.由①知,P(B)=P(X=2),P(C)=P(X=1),故P(A)=P(B∪C)=P(X=2)+P(X

=1)=67.所以,事件A发生的概率为67.考点116考点1176.(2017·全国3,理18,12分,难度★★)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处

理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数

据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数216362574以最高气温位于各区间的频率代替最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量X(单位:瓶)

的分布列;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?考点116考点117解(1)由题意知,X所有可能取值为200,300,500,由表

格数据知P(X=200)=2+1690=0.2,P(X=300)=3690=0.4,P(X=500)=25+7+490=0.4.因此X的分布列为X200300500P0.20.40.4(2)由题意知,这种酸奶一天的需求量至多为500,至少为2

00,因此只需考虑200≤n≤500.当300≤n≤500时,若最高气温不低于25,则Y=6n-4n=2n;若最高气温位于区间[20,25),则Y=6×300+2(n-300)-4n=1200-2n;若最高气温低于20,则Y=6×200+2(n-20

0)-4n=800-2n.因此EY=2n×0.4+(1200-2n)×0.4+(800-2n)×0.2=640-0.4n.考点116考点117当200≤n<300时,若最高气温不低于20,则Y=6n-4n=

2n;若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n.因此EY=2n×(0.4+0.4)+(800-2n)×0.2=160+1.2n.所以n=300时,Y的数学期望达到最大值,最

大值为520元.考点116考点1177.(2017·天津,理16,13分,难度★★)从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为12,13,14.(1)记X表

示一辆车从甲地到乙地遇到红灯的个数,求随机变量X的分布列和数学期望;(2)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.考点116考点117解(1)随机变量X的所有可能取值为0,1,2,3.P(X=0)=1-12×1-13×1-

14=14,P(X=1)=12×1-13×1-14+1-12×13×1-14+1-12×1-13×14=1124,P(X=2)=1-12×13×14+12×1-13×14+12×13×1-14=14,P(X=3)=12×13×14=124.所以,随机变量X的分布列为X0123P14112

414124随机变量X的数学期望E(X)=0×14+1×1124+2×14+3×124=1312.考点116考点117(2)设Y表示第一辆车遇到红灯的个数,Z表示第二辆车遇到红灯的个数,则所求事件的概率为P(Y+Z=1)=P(Y=0,Z=1)+P(Y=1,Z=

0)=P(Y=0)P(Z=1)+P(Y=1)P(Z=0)=14×1124+1124×14=1148.所以,这2辆车共遇到1个红灯的概率为1148.考点116考点1178.(2017·山东,理18,12分,难度★★)在心理学研究中,常采用对比试验的方法评价不同心理暗

示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示.通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,

A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.(1)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率.(2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.

考点116考点117解(1)记接受甲种心理暗示的志愿者中包含A1但不包含B1的事件为M,则P(M)=C84C105=518.(2)由题意知X可取的值为:0,1,2,3,4,则P(X=0)=C65C105=142,P(X=1)=C64C41C105=521,P(X=2)=C63C42C105=102

1,P(X=3)=C62C43C105=521,P(X=4)=C61C44C105=142.考点116考点117因此X的分布列为X01234P1425211021521142X的数学期望是EX=0×P(X=0)+1×P(X=

1)+2×P(X=2)+3×P(X=3)+4×P(X=4)=0+1×521+2×1021+3×521+4×142=2.在求离散型随机变量取某值的概率时,常常会用到古典概型求概率的问题,结合排列组合知识求得各对应概率,就转

化为常规的期望与方差题目.考点116考点1179.(2016·天津,理16,13分,难度★★)某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4,现从这10人中随机

选出2人作为该组代表参加座谈会.(1)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;(2)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列和数学期望.考点116考点117解(1)由已知,有P(A)=C

31C41+C32C102=13.所以,事件A发生的概率为13.(2)随机变量X的所有可能取值为0,1,2.P(X=0)=C32+C32+C42C102=415,P(X=1)=C31C31+C31C41C102=715

,P(X=2)=C31C41C102=415.所以,随机变量X的分布列为X012P415715415随机变量X的数学期望E(X)=0×415+1×715+2×415=1.考点116考点11710.(2015·天津,理16,13分,难度★★)为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员

组队参加.现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.(1)设A为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”,求事件A发生的概率;(2)设X为选

出的4人中种子选手的人数,求随机变量X的分布列和数学期望.考点116考点117解(1)由已知,有P(A)=C22C32+C32C32C84=635.所以,事件A发生的概率为635.(2)随机变量X的所有可能取值为1,2,3,4.P(X=k)=C5𝑘C

34-𝑘C84(k=1,2,3,4).所以,随机变量X的分布列为X1234P1143737114随机变量X的数学期望E(X)=1×114+2×37+3×37+4×114=52.考点116考点11711.(20

15·四川,理17,12分,难度★★)某市A,B两所中学的学生组队参加辩论赛,A中学推荐了3名男生、2名女生,B中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人、女生中随机抽取3人组成代表队.(1)求A中学至少有1名学生入选代表队

的概率;(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛.设X表示参赛的男生人数,求X的分布列和数学期望.考点116考点117解(1)由题意知,参加集训的男、女生各有6名.参赛学生全从B中学抽取(等价于A中学没有学生入选代表队)的概率为C33C43C63C63=11

00.因此,A中学至少有1名学生入选代表队的概率为1-1100=99100.(2)根据题意,X的可能取值为1,2,3.P(X=1)=C31C33C64=15,P(X=2)=C32C32C64=35,P(X=3)=C33C31C64=15.考点116考点117所以X的分布列为X123P153

515因此,X的数学期望为E(X)=1×P(X=1)+2×P(X=2)+3×P(X=3)=1×15+2×35+3×15=2.考点116考点11712.(2015·安徽,理17,12分,难度★★)已知2件次品和3件正品混放在一起,现

需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.(1)求第一次检测出的是次品且第二次检测出的是正品的概率;(2)已知每检测一件产品需要费用100

元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求X的分布列和均值(数学期望).考点116考点117解(1)记“第一次检测出的是次品且第二次检测出的是正品”为事件A,P(A)=A21A31A52=310

.(2)X的可能取值为200,300,400.P(X=200)=A22A52=110,P(X=300)=A33+C21C31A22A53=310,P(X=400)=1-P(X=200)-P(X=300)=1-110−310=61

0.故X的分布列为X200300400P110310610EX=200×110+300×310+400×610=350.考点116考点11713.(2015·福建,理16,13分,难度★★)某银行规定,一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定.小王到该银行

取钱时,发现自己忘记了银行卡的密码,但可以确认该银行卡的正确密码是他常用的6个密码之一.小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定.(1)求当天小王的该银行卡被锁定的概率;(2)设当天小

王用该银行卡尝试密码的次数为X,求X的分布列和数学期望.考点116考点117解(1)设“当天小王的该银行卡被锁定”的事件为A,则P(A)=56×45×34=12.(2)依题意得,X所有可能的取值是1,2,3.又P(X=1)=16,P(X=2)=

56×15=16,P(X=3)=56×45×1=23,所以X的分布列为X123P161623所以E(X)=1×16+2×16+3×23=52.考点116考点11714.(2013·全国1,理19,12分,难度★★)一批产品需要进行质量检验,

检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,

则这批产品通过检验;其他情况下,这批产品都不能通过检验.假设这批产品的优质品率为50%,即取出的每件产品是优质品的概率都为,且各件产品是否为优质品相互独立.(1)求这批产品通过检验的概率;(2)已知每件产品的检验费用为100元,且抽取的每件产

品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.12考点116考点117解(1)设第一次取出的4件产品中恰有3件优质品为事件A1,第一次取出的4件产品全是优质品为事件A2,第二次取出的4件产品都是优质品为事件B1,第二

次取出的1件产品是优质品为事件B2,这批产品通过检验为事件A,依题意有A=(A1B1)∪(A2B2),且A1B1与A2B2互斥,所以P(A)=P(A1B1)+P(A2B2)=P(A1)P(B1|A1)+P(A2)P(B2|A2)=416×116+116×12=364.(2)X可能的取值为400,5

00,800,并且P(X=400)=1-416−116=1116,P(X=500)=116,P(X=800)=14.所以X的分布列为X400500800P111611614EX=400×1116+50

0×116+800×14=506.25.考点116考点117考点117概率分布列与图表综合题1.(2017·北京,理17,13分,难度★★)为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患

者的生理指标x和y的数据,并制成下图,其中“􀆽”表示服药者,“+”表示未服药者.考点116考点117(1)从服药的50名患者中随机选出一人,求此人指标y的值小于60的概率;(2)从图中A,B,C,D四

人中随机选出两人,记ξ为选出的两人中指标x的值大于1.7的人数,求ξ的分布列和数学期望Eξ;(3)试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)考点116考点117解(1)由图知,在服药的50名患者中,指标y的值小于

60的有15人,所以从服药的50名患者中随机选出一人,此人指标y的值小于60的概率为1550=0.3.(2)由图知,A,B,C,D四人中,指标x的值大于1.7的有2人:A和C.所以ξ的所有可能取值为0,1,2.P(ξ=0)=C22C42=16,P(ξ=1)=C21C21C4

2=23,P(ξ=2)=C22C42=16.所以ξ的分布列为ξ012P162316故ξ的期望E(ξ)=0×16+1×23+2×16=1.(3)在这100名患者中,服药者指标y数据的方差大于未服药者指标y数据的方差.考点116考点1172.(2016·全国1,理19,12

分,难度★★)某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几

个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.考点116考点117(1)

求X的分布列;(2)若要求P(X≤n)≥0.5,确定n的最小值;(3)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?解(1)由柱状图并以频率代替概率可得,一台机器在三年内需更换的易损零件数为8,9,

10,11的概率分别为0.2,0.4,0.2,0.2.从而P(X=16)=0.2×0.2=0.04;P(X=17)=2×0.2×0.4=0.16;P(X=18)=2×0.2×0.2+0.4×0.4=0.24;P(X=19

)=2×0.2×0.2+2×0.4×0.2=0.24;P(X=20)=2×0.2×0.4+0.2×0.2=0.2;P(X=21)=2×0.2×0.2=0.08;P(X=22)=0.2×0.2=0.04.所以X的分布列为考点116考点11

7X16171819202122P0.040.160.240.240.20.080.04(2)由(1)知P(X≤18)=0.44,P(X≤19)=0.68,故n的最小值为19.(3)记Y表示2台机器在购买易损零件上所需的费用(单位:元).当n=19时,EY=19×200×0.68+(19×

200+500)×0.2+(19×200+2×500)×0.08+(19×200+3×500)×0.04=4040.当n=20时,EY=20×200×0.88+(20×200+500)×0.08+(20×200+2×500)×0.04

=4080.可知当n=19时所需费用的期望值小于n=20时所需费用的期望值,故应选n=19.考点116考点1173.(2016·全国2,理18,12分,难度★★)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下

:上年度出险次数01234≥5保费0.85aa1.25a1.5a1.75a2a设该险种一续保人一年内出险次数与相应概率如下:一年内出险次数01234≥5概率0.300.150.200.200.100.05(1)求一续保人本年度的保费高于

基本保费的概率;(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;(3)求续保人本年度的平均保费与基本保费的比值.考点116考点117解(1)设A表示事件:“一续保人本年度的保费高于基本保费”,则事件A发生当且仅当一年内出险次数大于1,故P(A

)=0.2+0.2+0.1+0.05=0.55.(2)设B表示事件:“一续保人本年度的保费比基本保费高出60%”,则事件B发生当且仅当一年内出险次数大于3,故P(B)=0.1+0.05=0.15.又P(AB)=P(B),故P(B|A)=𝑃(𝐴𝐵)𝑃

(𝐴)=𝑃(𝐵)𝑃(𝐴)=0.150.55=311.因此所求概率为311.(3)记续保人本年度的保费为X,则X的分布列为X0.85aa1.25a1.5a1.75a2aP0.300.150.200.200.100.05EX=0.85a×0.30+a×0.15+1

.25a×0.20+1.5a×0.20+1.75a×0.10+2a×0.05=1.23a.因此续保人本年度的平均保费与基本保费的比值为1.23.考点116考点1174.(2013·全国2,理19,12分,难度★★)经销商经销某种农产品,在一个销售季度内,每售

出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农

产品的利润.考点116考点117(1)将T表示为X的函数;(2)根据直方图估计利润T不少于57000元的概率;(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=10

5,且X=105的概率等于需求量落入[100,110)的频率),求T的数学期望.考点116考点117解(1)当X∈[100,130)时,T=500X-300(130-X)=800X-39000,当X∈[130,150]时,T=500×130=65000.所以T=800𝑋-39000,100≤�

�<130,65000,130≤𝑋≤150.(2)由(1)知利润T不少于57000元当且仅当120≤X≤150.由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T不少于57000元的概

率的估计值为0.7.(3)依题意可得T的分布列为T45000530006100065000P0.10.20.30.4所以ET=45000×0.1+53000×0.2+61000×0.3+65000×0.4=59400.考点116考点1175.(2013·北京,理16

,13分,难度★★)下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.(1)

求此人到达当日空气重度污染的概率;(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)考点116考点117解设Ai表示事件“此人于3月i日到达该

市”(i=1,2,…,13).根据题意,P(Ai)=113,且Ai∩Aj=⌀(i≠j).(1)设B为事件“此人到达当日空气重度污染”,则B=A5∪A8.所以P(B)=P(A5∪A8)=P(A5)+P(A8)=213.(2)由题意可知,X的所

有可能取值为0,1,2,且P(X=1)=P(A3∪A6∪A7∪A11)=P(A3)+P(A6)+P(A7)+P(A11)=413,P(X=2)=P(A1∪A2∪A12∪A13)=P(A1)+P(A2)+P(A12)+P(

A13)=413,P(X=0)=1-P(X=1)-P(X=2)=513.所以X的分布列为X012P513413413故X的数学期望EX=0×513+1×413+2×413=1213.(3)从3月5日开始连续

三天的空气质量指数方差最大.考点116考点1176.(2012·全国,理18,12分,难度★★)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.(1)若花店一天购进16枝玫瑰花,求

当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:日需求量n14151617181920频数10201616151310以100天记录的各需求量的频率作为各需求量

发生的概率.①若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列、数学期望及方差;②若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.考点116考点117解(1

)当日需求量n≥16时,利润y=80.当日需求量n<16时,利润y=10n-80.所以y关于n的函数解析式为y=10𝑛-80,𝑛<16,80,𝑛≥16(n∈N).(2)①X可能的取值为60,70,80,并且P(X=60)=0.1,P(X=70

)=0.2,P(X=80)=0.7.X的分布列为X607080P0.10.20.7X的数学期望为EX=60×0.1+70×0.2+80×0.7=76.X的方差为DX=(60-76)2×0.1+(70-76)2×0.2+(80-76)2×0.7=44.

考点116考点117②答案一:花店一天应购进16枝玫瑰花.理由如下:若花店一天购进17枝玫瑰花,Y表示当天的利润(单位:元),那么Y的分布列为Y55657585P0.10.20.160.54Y的数学期望为EY=55×0.1+65×0.2+75×0.16+85×0.54=76.4.Y的方差为D

Y=(55-76.4)2×0.1+(65-76.4)2×0.2+(75-76.4)2×0.16+(85-76.4)2×0.54=112.04.由以上的计算结果可以看出,DX<DY,即购进16枝玫瑰花时利润波动相对较小.另外,虽然EX<EY,但两者相差不

大.故花店一天应购进16枝玫瑰花.考点116考点117答案二:花店一天应购进17枝玫瑰花.理由如下:若花店一天购进17枝玫瑰花,Y表示当天的利润(单位:元),那么Y的分布列为Y55657585P0.10.20.160.54Y的数学期望为EY=55×0.1+65×0.2+7

5×0.16+85×0.54=76.4.由以上的计算结果可以看出,EX<EY,即购进17枝玫瑰花时的平均利润大于购进16枝时的平均利润.故花店一天应购进17枝玫瑰花.考点116考点1177.(2011·全国,理19,12分,难度★★)某种产品的质量以其质量指标值衡量,质量指标

值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:A配方的频数分布

表指标值分组[90,94)[94,98)[98,102)[102,106)[106,110]频数82042228B配方的频数分布表指标值分组[90,94)[94,98)[98,102)[102,106)[106,110]频数412

423210考点116考点117(1)分别估计用A配方,B配方生产的产品的优质品率;(2)已知用B配方生产的一件产品的利润y(单位:元)与其质量指标值t的关系式为y=-2,𝑡<94,2,94≤𝑡<102,4,𝑡≥102.从用B配方生产的产品中任取一件,其利润记为X(单位:

元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)考点116考点117解(1)由试验结果知,用A配方生产的产品中优质品的频率为22+8100=0.3,所以用A配方生产的产品的优质品率的估计值为0.3.由试验结果知,用B配方生

产的产品中优质品的频率为32+10100=0.42,所以用B配方生产的产品的优质品率的估计值为0.42.(2)用B配方生产的100件产品中,其质量指标值落入区间[90,94),[94,102),[102,110]的频率

分别为0.04,0.54,0.42,因此P(X=-2)=0.04,P(X=2)=0.54,P(X=4)=0.42,即X的分布列为X-224P0.040.540.42X的数学期望E(X)=-2×0.04+2×0.54+4×0.42=2.68.