【文档说明】2020高考数学大一轮复习指导课件第四章平面向量与解三角形44解三角形的应用.ppt，共(51)页，2.145 MB，由小橙橙上传

转载请保留链接：https://www.ichengzhen.cn/view-256674.html

以下为本文档部分文字说明：

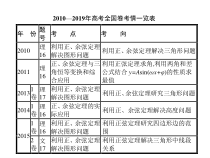
2010—2019年高考全国卷考情一览表年份题号考点考向2010理16利用正、余弦定理解决图形问题利用正、余弦定理解决三角形问题2011理16正、余弦定理与三角恒等变换和综合应用利用正弦定理求角,利用

两角和差公式结合y=Asin(ωx+φ)的性质求最值20131卷理17利用正、余弦定理解决图形问题利用正、余弦定理研究三角形问题20141卷理16正、余弦定理的实际应用利用正、余弦定理解决高度问题20151卷理16利用正、

余弦定理解决图形问题利用正弦定理研究四边形边的范围2卷文17利用正、余弦定理解决图形问题利用正弦定理解决三角形中线段关系年份题号考点考向20171卷文11正、余弦定理与三角恒等变换的综合应用根据两角和差公式结合正弦定理求角20191卷文11正、余弦定理与三角恒等变换的综合应用正、余弦

定理的综合应用3卷理18文18正、余弦定理与三角恒等变换的综合应用求角的度数及三角形面积的取值范围考情分析与预测1.高考常考内容,属中档题,高考对本节的考查主要有三个方面:(1)正余弦定理与三角恒等变换的综合应用:解三角

形、边角统一思想与三角恒等变换的综合应用求角的三角函数值或者范围;(2)利用正余弦定理解决图形问题:分析给出的图形,将已知条件先集中到某个三角形中,解三角形,再依次解其他三角形,直至求出结果;(3)正余弦定理的实际应用:建立三角函数模型,利用解三角形公式求出边或角.2.

2020年高考对本节的考查不会有大的变化,仍是考查正余弦定理与三角恒等变换的综合应用以及解决图形中的边角问题.考点54考点55考点56考点54正、余弦定理与三角恒等变换的综合应用1.(2019·全国1,文11,5分,难度★

★)△ABC的内角A,B,C的对边分别为a,b,c.已知asinA-bsinB=4csinC,cosA=-14,则𝑏𝑐=(A)A.6B.5C.4D.3解析由已知及正弦定理,得a2-b2=4c2,由余弦定理的

推论,得-14=cosA=𝑏2+𝑐2-𝑎22𝑏𝑐,∴𝑐2-4𝑐22𝑏𝑐=-14,∴-3𝑐2𝑏=-14,∴𝑏𝑐=32×4=6,故选A.考点54考点55考点562.(2017·全国1,文11,5分,难度★★)△ABC的内角A,B,C的对边分别为a,b

,c.已知sinB+sinA(sinC-cosC)=0,a=2,c=2,则C=(B)A.π12B.π6C.π4D.π3解析由题意结合三角形的内角和,可得sin(A+C)+sinA(sinC-cosC)=0,整理得sinAcosC+cosA

sinC+sinAsinC-sinAcosC=0,则sinC(sinA+cosA)=0,因为sinC>0,所以sinA+cosA=0,即tanA=-1,因为A∈(0,π),所以A=3π4.由正弦定理𝑎sin𝐴=𝑐sin�

�,得2sin3π4=2sin𝐶,即sinC=12,所以C=π6,故选B.注意转化与化归思想在解三角形中的应用;如本题中已知条件中角A,B,C都存在,则需利用A+B+C=π消去其中一个角,转化为可利用两

角和差公式的形式.考点54考点55考点563.(2018·全国1,文16,5分,难度★★★)△ABC的内角A,B,C的对边分别为a,b,c,已知bsinC+csinB=4asinBsinC,b2+c2-a2=8,则△ABC的面积为.233解析∵bsinC+csinB

=4asinBsinC,∴sinBsinC+sinCsinB=4sinAsinBsinC.又sinBsinC>0,∴sinA=12.由余弦定理得cosA=𝑏2+𝑐2-𝑎22𝑏𝑐=82𝑏𝑐=4𝑏𝑐>0,∴c

osA=32,bc=4cos𝐴=833,∴S△ABC=12bcsinA=12×833×12=233.考点54考点55考点564.(2011·全国,理16,5分,难度★★)在△ABC中,B=60°,AC=3,则AB+2BC的最大值为27.解析令AB=c,BC=a,则由正弦定

理得𝑎sin𝐴=𝑐sin𝐶=𝐴𝐶sin𝐵=332=2,则c=2sinC,a=2sinA,且A+C=120°,AB+2BC=c+2a=2sinC+4sinA=2sinC+4sin(120°-C)=2sinC+432cos𝐶+12sin𝐶=4sinC+23cosC=27sin(

C+φ)其中tan𝜑=32.故当C+φ=90°时,AB+2BC取最大值27.求边的最值问题一般利用正弦定理转化为角的关系,利用三角函数性质求最值.考点54考点55考点565.(2019·全国3,理1

8文18,12分,难度★★)△ABC的内角A,B,C的对边分别为a,b,c.已知asin=bsinA.(1)求B;(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.𝐴+𝐶2解(1)由题设及正弦定理

得sinAsin𝐴+𝐶2=sinBsinA.因为sinA≠0,所以sin𝐴+𝐶2=sinB.由A+B+C=180°,可得sin𝐴+𝐶2=cos𝐵2,故cos𝐵2=2sin𝐵2cos𝐵2.因为cos𝐵2≠0,故sin𝐵2=

12,因此B=60°.考点54考点55考点56(2)由题设及(1)知△ABC的面积S△ABC=34a.由正弦定理得a=𝑐sin𝐴sin𝐶=sin(120°-𝐶)sin𝐶=32tan𝐶+12.由于△

ABC为锐角三角形,故0°<A<90°,0°<C<90°.由(1)知A+C=120°,所以30°<C<90°,故12<a<2,从而38<S△ABC<32.因此,△ABC面积的取值范围是38,32.考点54考点55考点566.(2019·天津,理15文16,13分,难度★★)

在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2a,3csinB=4asinC.(1)求cosB的值;(2)求sin2B+π6的值.解(1)在△ABC中,由正弦定理𝑏sin𝐵=𝑐sin𝐶,得bsinC=csinB,又由3csinB=4asinC,得3bsinC

=4asinC,即3b=4a.又因为b+c=2a,得到b=43a,c=23a.由余弦定理可得cosB=𝑎2+𝑐2-𝑏22𝑎𝑐=𝑎2+49𝑎2-169𝑎22·𝑎·23𝑎=-14.(2)由(1)可得sin

B=1-cos2𝐵=154,从而sin2B=2sinBcosB=-158,cos2B=cos2B-sin2B=-78,故sin2B+π6=sin2Bcosπ6+cos2Bsinπ6=-158×32−78

×12=-35+716.考点54考点55考点56本小题主要考查同角三角函数的基本关系,两角和的正弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识.考查运算求解能力.考点54考点55考点567.(2019·江苏,15,14分,难度★★)在△ABC中,角A,B,C的对

边分别为a,b,c.(1)若a=3c,b=2,cosB=23,求c的值;(2)若sin𝐴𝑎=cos𝐵2𝑏,求sin𝐵+π2的值.考点54考点55考点56解(1)因为a=3c,b=2,cosB=23,由余弦定理cosB=𝑎2+𝑐2-

𝑏22𝑎𝑐,得23=(3𝑐)2+𝑐2-(2)22×3𝑐×𝑐,即c2=13.所以c=33.(2)因为sin𝐴𝑎=cos𝐵2𝑏,由正弦定理𝑎sin𝐴=𝑏sin𝐵,得cos𝐵2𝑏=sin𝐵𝑏,所以cosB=2sinB.从而cos2B=(2sinB)2,即cos2B=

4(1-cos2B),故cos2B=45.因为sinB>0,所以cosB=2sinB>0,从而cosB=255.因此sin𝐵+π2=cosB=255.考点54考点55考点568.(2018·天津,理15文16,

13分,难度★★)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知bsinA=acos.(1)求角B的大小;(2)设a=2,c=3,求b和sin(2A-B)的值.𝐵-π6解(1)在△ABC中,由正弦定理𝑎sin𝐴=𝑏sin𝐵,可得bs

inA=asinB.又由bsinA=acos𝐵-π6,得asinB=acos𝐵-π6,即sinB=cos𝐵-π6,可得tanB=3.又因为B∈(0,π),所以B=π3.(2)在△ABC中,由余弦定理及a=2,c=3,B

=π3,有b2=a2+c2-2accosB=7,故b=7.由bsinA=acos𝐵-π6,可得sinA=37.因为a<c,故cosA=27.因此sin2A=2sinAcosA=437,cos2A=2cos2A-1=17.所以,sin(2A-B)=sin2AcosB-co

s2AsinB=437×12−17×32=3314.考点54考点55考点569.(2017·天津,理15,12分,难度★★)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知a>b,a=5,c=6,sinB=.(1)求

b和sinA的值;(2)求sin的值.352𝐴+π4解(1)在△ABC中,因为a>b,故由sinB=35,可得cosB=45.由已知及余弦定理,有b2=a2+c2-2accosB=13,所以b=13.由正弦定理𝑎sin𝐴=𝑏

sin𝐵,得sinA=𝑎sin𝐵𝑏=31313.所以,b的值为13,sinA的值为31313.(2)由(1)及a<c,得cosA=21313,所以sin2A=2sinAcosA=1213,cos2A=1-2sin2A=-513.故sin2𝐴+π4=sin2A

cosπ4+cos2Asinπ4=7226.考点54考点55考点5610.(2017·天津,文15,12分,难度★★)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知asinA=4bsinB,ac=(a2-b2-c2).(1)求co

sA的值;(2)求sin(2B-A)的值.5考点54考点55考点56解(1)由asinA=4bsinB,及𝑎sin𝐴=𝑏sin𝐵,得a=2b.由ac=5(a2-b2-c2),及余弦定理,得cosA=𝑏2+𝑐2-𝑎22𝑏𝑐=-55𝑎𝑐𝑎𝑐=

-55.(2)由(1),可得sinA=255,代入asinA=4bsinB,得sinB=𝑎sin𝐴4𝑏=55.由(1)知,A为钝角,所以cosB=1-sin2𝐵=255.于是sin2B=2sinBcosB=45,cos2B=1

-2sin2B=35,故sin(2B-A)=sin2BcosA-cos2BsinA=45×-55−35×255=-255.考点54考点55考点5611.(2016·北京,理15,12分,难度★★)在△

ABC中,a2+c2=b2+ac.(1)求B的大小;(2)求cosA+cosC的最大值.22解(1)由余弦定理及题设得cosB=𝑎2+𝑐2-𝑏22𝑎𝑐=2𝑎𝑐2𝑎𝑐=22.又因为0<B<π,所以B=π4.(2)由(1)知A+C=3π4.2cosA+cosC=2cosA+cos3π

4-𝐴=2cosA-22cosA+22sinA=22cosA+22sinA=cos𝐴-π4.因为0<A<3π4,所以当A=π4时,2cosA+cosC取得最大值1.考点54考点55考点5612.(2016·山东,理16,12分,难度★★)在△ABC中,角A,B,C的对边分别为a,b,c,已知

2(tanA+tanB)=tan𝐴cos𝐵+tan𝐵cos𝐴.(1)证明:a+b=2c;(2)求cosC的最小值.(1)证明由题意知2sin𝐴cos𝐴+sin𝐵cos𝐵=sin𝐴cos𝐴cos𝐵+sin𝐵cos�

�cos𝐵,化简得2(sinAcosB+sinBcosA)=sinA+sinB,即2sin(A+B)=sinA+sinB,因为A+B+C=π,所以sin(A+B)=sin(π-C)=sinC.从而sinA+sinB=2sinC.由正弦定理得a+b=2c.(2)解由(1)

知c=𝑎+𝑏2,所以cosC=𝑎2+𝑏2-𝑐22𝑎𝑏=𝑎2+𝑏2-𝑎+𝑏222𝑎𝑏=38𝑎𝑏+𝑏𝑎−14≥12,当且仅当a=b时,等号成立.故cosC的最小值为12.考点54考点55考点5613.

(2016·天津,文15,12分,难度★★)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asin2B=bsinA.(1)求B;(2)若cosA=,求sinC的值.313解(1)在△ABC中,由𝑎s

in𝐴=𝑏sin𝐵,可得asinB=bsinA,又由asin2B=3bsinA,得2asinBcosB=3bsinA=3asinB,所以cosB=32,得B=π6.(2)由cosA=13,可得sinA=223,则sinC=

sin[π-(A+B)]=sin(A+B)=sin𝐴+π6=32sinA+12cosA=26+16.考点54考点55考点5614.(2015·江苏,理15,12分,难度★★)在△ABC中,已知AB=2,AC=3,A=

60°.(1)求BC的长;(2)求sin2C的值.解(1)由余弦定理知,BC2=AB2+AC2-2AB·AC·cosA=4+9-2×2×3×12=7,所以BC=7.(2)由正弦定理知,𝐴𝐵sin𝐶=𝐵𝐶sin𝐴,所以sinC

=𝐴𝐵𝐵𝐶·sinA=2sin60°7=217.因为AB<BC,所以C为锐角,则cosC=1-sin2𝐶=1-37=277.因此sin2C=2sinC·cosC=2×217×277=437.考点54考点55考点5615.

(2015·浙江,文16,12分,难度★★)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知tanπ4+𝐴=2.(1)求sin2𝐴sin2𝐴+cos2𝐴的值;(2)若B=π4,a=3,求△ABC的面积.解(1)由tanπ4+𝐴=2,得tanA=13,所以sin2�

�sin2𝐴+cos2𝐴=2tan𝐴2tan𝐴+1=25.(2)由tanA=13,A∈(0,π),得sinA=1010,cosA=31010.又由a=3,B=π4及正弦定理𝑎sin𝐴=𝑏sin𝐵,得b=3

5.由sinC=sin(A+B)=sin𝐴+π4得sinC=255.设△ABC的面积为S,则S=12absinC=9.考点54考点55考点5616.(2015·天津,文16,12分,难度★★)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知

△ABC的面积为315,b-c=2,cosA=-14.(1)求a和sinC的值;(2)求cos2𝐴+π6的值.解(1)在△ABC中,由cosA=-14,可得sinA=154.由S△ABC=12bcsinA=315,得bc=24,又由b-c=2,解得b=6,c=4.由a2=b2+c2-2bcco

sA,可得a=8.由𝑎sin𝐴=𝑐sin𝐶,得sinC=158.(2)cos2𝐴+π6=cos2A·cosπ6-sin2A·sinπ6=32(2cos2A-1)-12×2sinA·cosA=15-7316.考点54考点55考点5617.(2014·辽宁,理17,12分,难度★★

)在△ABC中,内角A,B,C的对边分别为a,b,c,且a>c.已知𝐵𝐴·𝐵𝐶=2,cosB=13,b=3.求:(1)a和c的值;(2)cos(B-C)的值.解(1)由𝐵𝐴·𝐵𝐶=2,得c·acosB=2.又cosB=13,所以a

c=6.由余弦定理,得a2+c2=b2+2accosB.又b=3,所以a2+c2=9+2×2=13.解𝑎𝑐=6,𝑎2+𝑐2=13,得a=2,c=3或a=3,c=2.因a>c,所以a=3,c=2.考点54考点55考点56(2)在△ABC中,

sinB=1-cos2𝐵=1-132=223,由正弦定理,得sinC=𝑐𝑏sinB=23×223=429.因a=b>c,所以C为锐角,因此cosC=1-sin2𝐶=1-4292=79.于是cos(B-C)=cosBcosC+sinBsinC=13×79+223×429=

2327.考点54考点55考点5618.(2014·天津,文16,12分,难度★★)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a-c=66b,sinB=6sinC.(1)求cosA的值;(2)求cos2𝐴-π6的值.考点54考点55

考点56解(1)在△ABC中,由𝑏sin𝐵=𝑐sin𝐶,及sinB=6sinC,可得b=6c.又由a-c=66b,有a=2c.所以,cosA=𝑏2+𝑐2-𝑎22𝑏𝑐=6𝑐2+𝑐2-4𝑐226𝑐2=64.(2)在△ABC中,由cosA=64,可

得sinA=104.于是cos2A=2cos2A-1=-14,sin2A=2sinA·cosA=154.所以,cos2𝐴-π6=cos2A·cosπ6+sin2A·sinπ6=15-38.考点54考点55考点56考点

55利用正、余弦定理解决图形问题1.(2019·浙江,14,6分,难度★★)在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上.若∠BDC=45°,则BD=,cos∠ABD=.12257210考点54考点55考点56解析如图所示,设CD=x,∠DBC=α,则A

D=5-x,∠ABD=π2-α,在△BDC中,由正弦定理得3sinπ4=𝑥sin𝛼=32⇒sinα=𝑥32.在△ABD中,由正弦定理得5-𝑥sin(π2-𝛼)=4sin3π4=42⇒cosα=5-𝑥

42.由sin2α+cos2α=𝑥218+(5-𝑥)232=1,解得x1=-35(舍去),x2=215⇒BD=1225.在△ABD中,由正弦定理得0.8sin∠𝐴𝐵𝐷=4sin(π-π4)⇒sin∠ABD=210⇒cos∠ABD=7210.

考点54考点55考点562.(2017·浙江,14,5分,难度★★)已知△ABC,AB=AC=4,BC=2.点D为AB延长线上一点,BD=2,连接CD,则△BDC的面积是,cos∠BDC=.152104解析依题意作出图形,如图所示

,则sin∠DBC=sin∠ABC.由题意知AB=AC=4,BC=BD=2,则sin∠ABC=154,cos∠ABC=14.所以S△BDC=12BC·BD·sin∠DBC=12×2×2×154=152.因为cos∠DBC=-cos∠ABC=-14=𝐵𝐷2+𝐵𝐶2-𝐶𝐷22𝐵�

�·𝐵𝐶=8-𝐶𝐷28,所以CD=10.由余弦定理,得cos∠BDC=4+10-42×2×10=104.解决多边形问题时,通常从多边形中,选择一个条件集中的三角形求解,然后利用其结果,解其他三角形,直至确定要求的量.考点54

考点55考点563.(2015·全国1,理16,5分,难度★★)在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是.6−2,6+2解析如图.作CE∥AD交AB于E,则∠CEB=75°,∠ECB=30°.在

△CBE中,由正弦定理得,EB=6−2.延长CD交BA的延长线于F,则∠F=30°.在△BCF中,由正弦定理得,BF=6+2,所以AB的取值范围为(6−2,6+2).考点54考点55考点564.(2015·重庆,理13,5分,难度★★)在△ABC中,B=12

0°,AB=2,A的角平分线AD=3,则AC=6.解析如图所示,在△ABD中,由正弦定理,得𝐴𝐷sin𝐵=𝐴𝐵sin∠𝐴𝐷𝐵,即3sin120°=2sin∠𝐴𝐷𝐵,所以sin∠ADB=22,可得∠ADB=

45°,则∠BAD=∠DAC=15°.所以∠ACB=30°,∠BAC=30°.所以△BAC是等腰三角形,BC=AB=2.由余弦定理,得AC=𝐴𝐵2+𝐵𝐶2-2·𝐴𝐵·𝐵𝐶·cos120°=(2)2+(2)2-2×2×2×-12=6.考点54考点55考点565.

(2010·全国,理16,5分,难度★★)在△ABC中,D为边BC上一点,BD=DC,∠ADB=120°,AD=2.若△ADC的面积为3-,则∠BAC=60°.123解析由S△ADC=12×2×DC×32=3-3,解

得DC=2(3-1),则BD=3-1,BC=3(3-1).∵在△ABD中,AB2=4+(3-1)2-2×2×(3-1)×cos120°=6,∴AB=6.在△ACD中,AC2=4+[2(3-1)]2-2×2×2(3-1)×cos60°=24-123,∴AC=6(

3-1).则cos∠BAC=𝐴𝐵2+𝐴𝐶2-𝐵𝐶22𝐴𝐵·𝐴𝐶=6+24-123-9(4-23)2×6×6×(3-1)=12,∴∠BAC=60°.考点54考点55考点566.(2018·全国

1,理17,12分,难度★★)在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.(1)求cos∠ADB;(2)若DC=2,求BC.2解(1)在△ABD中,由正弦定理得𝐵𝐷sin∠𝐴=𝐴𝐵sin∠�

�𝐷𝐵.由题设知,5sin45°=2sin∠𝐴𝐷𝐵,所以sin∠ADB=25.由题设知,∠ADB<90°,所以cos∠ADB=1-225=235.(2)由题设及(1)知,cos∠BDC=sin∠ADB=25.在△BCD中,由余弦定理得BC2=BD2+DC2-2·BD·DC·cos∠B

DC=25+8-2×5×22×25=25.所以BC=5.考点54考点55考点567.(2018·北京,理15,13分,难度★★)在△ABC中,a=7,b=8,cosB=-.(1)求∠A;(2)求AC边上的高.17考点54考点55考点56(2)在△ABC中,sinC=

sin(A+B)=sinAcosB+sinBcosA=32×-17+12×437=3314.如图所示,在△ABC中,过点B作BD⊥AC于点D.∵sinC=ℎ𝐵𝐶,∴h=BC·sinC=7×3314=332,∴AC边上的高为332.解(1)在△ABC中,∵cosB=-17,∴

B∈π2,π,∴sinB=1-cos2𝐵=437.由正弦定理,得𝑎sin𝐴=𝑏sin𝐵⇒7sin𝐴=8437,∴sinA=32.∵B∈π2,π,∴A∈0,π2,∴A=π3.考点54考点55考点568.(2015·全国2,文17,10分,难度★★)△ABC中,D是BC上的点

,AD平分∠BAC,BD=2DC.(1)求;(2)若∠BAC=60°,求∠B.sin𝐵sin𝐶解(1)由正弦定理得𝐴𝐷sin𝐵=𝐵𝐷sin∠𝐵𝐴𝐷,𝐴𝐷sin𝐶=𝐷𝐶sin∠𝐶𝐴𝐷.因为A

D平分∠BAC,BD=2DC,所以sin𝐵sin𝐶=𝐷𝐶𝐵𝐷=12.(2)因为∠C=180°-(∠BAC+∠B),∠BAC=60°,所以sinC=sin(∠BAC+∠B)=32cosB+12sinB.由(1)知2sinB=sinC,所以tanB=33,即∠B=30

°.考点54考点55考点569.(2015·安徽,理16,12分,难度★★)在△ABC中,∠A=3π4,AB=6,AC=32,点D在BC边上,AD=BD,求AD的长.解设△ABC的内角A,B,C所对边的长分别是a,b,c.由余弦定理得a2=b2+c2-2bccos∠BAC=(32)

2+62-2×32×6×cos3π4=18+36-(-36)=90,所以a=310.又由正弦定理得sinB=𝑏sin∠𝐵𝐴𝐶𝑎=3310=1010,由题设知0<B<π4,所以cosB=1-sin2𝐵=1-110=31010.在△ABD中,由正弦定理得AD

=𝐴𝐵·sin𝐵sin(π-2𝐵)=6sin𝐵2sin𝐵cos𝐵=3cos𝐵=10.考点54考点55考点5610.(2014·北京,理15,13分,难度★★)如图,在△ABC中,∠B=,AB=8,点D在BC边上,且CD=2,cos∠ADC=.(1)求sin∠BAD;(2)求BD,

AC的长.π317解(1)在△ADC中,因为cos∠ADC=17,所以sin∠ADC=437.所以sin∠BAD=sin(∠ADC-∠B)=sin∠ADCcosB-cos∠ADCsinB=437×12−17×32=3314.(2)在△ABD中,由正弦定理,得BD=𝐴𝐵·sin∠𝐵𝐴𝐷

sin∠𝐴𝐷𝐵=8×3314437=3.在△ABC中,由余弦定理得AC2=AB2+BC2-2AB·BC·cosB=82+52-2×8×5×12=49.所以AC=7.考点54考点55考点5611.(2014·湖南,理18,12分,难度★★)如

图,在平面四边形ABCD中,AD=1,CD=2,AC=7.(1)求cos∠CAD的值;(2)若cos∠BAD=-714,sin∠CBA=216,求BC的长.解(1)如题图,在△ADC中,由余弦定理,得co

s∠CAD=𝐴𝐶2+𝐴𝐷2-𝐶𝐷22𝐴𝐶·𝐴𝐷.故由题设知,cos∠CAD=7+1-427=277.考点54考点55考点56(2)如题图,设∠BAC=α,则α=∠BAD-∠CAD.因为cos∠CAD=277,cos∠BAD=-714,所

以sin∠CAD=1-cos2∠𝐶𝐴𝐷=1-2772=217,sin∠BAD=1-cos2∠𝐵𝐴𝐷=1--7142=32114.于是sinα=sin(∠BAD-∠CAD)=sin∠BADcos∠CAD-cos∠BADsin∠CAD=32114×277−-714×

217=32.在△ABC中,由正弦定理,𝐵𝐶sin𝛼=𝐴𝐶sin∠𝐶𝐵𝐴.故BC=𝐴𝐶·sin𝛼sin∠𝐶𝐵𝐴=7×32216=3.考点54考点55考点5612.(2014·湖南,文19,12分,难度★★)如图,在平面四边形ABCD

中,DA⊥AB,DE=1,EC=7,EA=2,∠ADC=2π3,∠BEC=π3.(1)求sin∠CED的值;(2)求BE的长.解如题图,设∠CED=α.(1)在△CDE中,由余弦定理,得EC2=CD2+DE2-2CD·DE·cos∠EDC.于是由题设

知,7=CD2+1+CD,即CD2+CD-6=0.解得CD=2(CD=-3舍去).在△CDE中,由正弦定理,得𝐸𝐶sin∠𝐸𝐷𝐶=𝐶𝐷sin𝛼.考点54考点55考点56于是,sinα=𝐶𝐷·sin2π3𝐸𝐶=2×327=217,即sin∠CED=217.(2)

由题设知,0<α<π3,于是由(1)知,cosα=1-sin2𝛼=1-2149=277.而∠AEB=2π3-α,所以cos∠AEB=cos2π3-𝛼=cos2π3cosα+sin2π3sinα=-12cosα

+32sinα=-12×277+32×217=714.在Rt△EAB中,cos∠AEB=𝐸𝐴𝐵𝐸=2𝐵𝐸,故BE=2cos∠𝐴𝐸𝐵=2714=47.考点54考点55考点5613.(2013·全国1,理17,12分,难度★★)如图,在△ABC中,∠ABC=

90°,AB=,BC=1,P为△ABC内一点,∠BPC=90°.(1)若PB=,求PA;(2)若∠APB=150°,求tan∠PBA.12解(1)由已知得∠PBC=60°,所以∠PBA=30°.在△PBA中,由余弦定理得PA2=3+14-2×3×12cos30°=74.故PA=

72.(2)设∠PBA=α,由已知得PB=sinα.在△PBA中,由正弦定理得3sin150°=sin𝛼sin(30°-𝛼),化简得3cosα=4sinα.所以tanα=34,即tan∠PBA=34.3考点54考点55考点56考点56正、余弦定理的实际应用1.(2014·四川,文8

,5分,难度★★)如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于(C)A.240(3-1)mB.180(2-1)mC.120(3-1)mD.30(3+1)m考点54考点55

考点56解析如图,作AD⊥BC,垂足为D.由题意,得DC=60×tan60°=603(m),DB=60×tan15°=60×tan(45°-30°)=60×tan45°-tan30°1+tan45°tan30°=60×

1-331+33=(120-603)m.所以BC=DC-DB=603-(120-603)=1203-120=120(3-1)(m),故选C.考点54考点55考点562.(2015·湖北,理13文15,5分,难度★★★)如

图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=100m.6考点54考点55考点56解析如图所示,由已知得∠BAC=30°,AB=600m,∠EBC=

75°,∠CBD=30°.在△ABC中,∠ACB=∠EBC-∠BAC=45°,由𝐵𝐶sin∠𝐵𝐴𝐶=𝐴𝐵sin∠𝐴𝐶𝐵,得BC=𝐴𝐵·sin∠𝐵𝐴𝐶sin∠𝐴𝐶𝐵=600×1222=3002(m).在Rt△

BCD中,CD=BC·tan∠CBD=3002×33=1006(m).考点54考点55考点563.(2014·全国1,理16,5分,难度★★)如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及

∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=150m.考点54考点55考点56解析在Rt△ABC中,由于∠CAB=45°,BC=100m,所以AC=1002m.在△MAC中,∠AMC=180°-75°-60°=45°,由正弦定理

可得𝐴𝐶sin∠𝐴𝑀𝐶=𝑀𝐴sin∠𝑀𝐶𝐴,于是MA=1002×3222=1003(m).在Rt△MNA中,∠MAN=60°,于是MN=MA·sin∠MAN=1003×32=150(m),即山高MN=150m.考点54考点55考点564.(2010

·陕西,理17,12分,难度★★★)如图,A,B是海面上位于东西方向相距5(3+)海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20海里的C点的救援船立即前往营救,其航行速度为30海里/时,该救援船到达D点需要

多长时间?33考点54考点55考点56解由题意知AB=5(3+3)海里,∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,∴∠ADB=180°-(45°+30°)=105°.在△DAB中,由正弦定理得𝐷𝐵sin∠𝐷𝐴𝐵=𝐴𝐵sin∠𝐴

𝐷𝐵,∴DB=𝐴𝐵·sin∠𝐷𝐴𝐵sin∠𝐴𝐷𝐵=5(3+3)·sin45°sin105°=5(3+3)·sin45°sin45°cos60°+cos45°sin60°=53(3+1)3+12=103(海

里).又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=203海里,在△DBC中,由余弦定理,得CD2=BD2+BC2-2BD·BC·cos∠DBC=300+1200-2×103×203×12=900,∴CD=30(海里),则需要的时间t=3030=1(小时).答:救援船

到达D点需要1小时.