轴对称全章复习与巩固（提高）【学习目标】1.认识轴对称、轴对称图形，理解轴对称的基本性质及它们的简单应用；2.了解垂直平分线的概念，并掌握其性质；3.了解等腰三角形、等边三角形的有关概念，并掌握它们的性质以及判定方法.【知识网络】【要点梳理】【高清课堂：389304轴对称复习，本章概述】要点一、轴对称1.轴对称图形和轴对称（1）轴对称图形如果一个图形沿着某一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴.轴对称图形的性质：轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线.（2）轴对称定义：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴.成轴对称的两个图形的性质：①关于�

一元一次方程的解法（基础）知识讲解【学习目标】1.熟悉解一元一次方程的一般步骤，理解每步变形的依据；2.掌握一元一次方程的解法，体会解法中蕴涵的化归思想；3.进一步熟练掌握在列方程时确定等量关系的方法.【要点梳理】要点一、解一元一次方程的一般步骤变形名称具体做法注意事项去分母在方程两边都乘以各分母的最小公倍数(1)不要漏乘不含分母的项(2)分子是一个整体的，去分母后应加上括号去括号先去小括号，再去中括号，最后去大括号(1)不要漏乘括号里的项(2)不要弄错符号移项把含有未知数的项都移到方程的一边，其他项都移到方程的另一边(记住移项要变号)(1)移项要变号(2)不要丢项合并同类项把方程化成ax＝b(a≠0)的形式字母及其指数不变系数化成1在方程两边都除以未知数的系数a，得到方程的解bxa．不要把分子、分母写颠�

等边三角形（基础）【学习目标】1.掌握等边三角形的性质和判定.2.掌握含30°角的直角三角形的一个主要性质．3.熟练运用等边三角形的判定定理与性质定理进行推理和计算．【要点梳理】【高清课堂：389303等边三角形，知识要点】要点一、等边三角形等边三角形定义：三边都相等的三角形叫等边三角形.要点诠释：由定义可知，等边三角形是一种特殊的等腰三角形．也就是说等腰三角形包括等边三角形．要点二、等边三角形的性质等边三角形的性质：等边三角形三个内角都相等，并且每一个内角都等于60°.要点三、等边三角形的判定等边三角形的判定：（1）三条边都相等的三角形是等边三角形；（2）三个角都相等的三角形是等边三角形；（3）有一个角是60°的等腰三角形是等边三角形．要点四、含30°的直角三角形含30°的直角三角形的性质定理�

2022－2023年人教版数学七年级上册1.4.1《有理数的乘法》课时练习一、选择题1.与－2的乘积为1的数是()A.2B.－2C.12D.－122.计算（﹣3）×3的结果是（）A.﹣9B.9C.0D.﹣63.下列说法错误的是()A.一个数同0相乘，仍得0B.一个数同1相乘，仍得原数C.一个数同－1相乘得原数的相反数D.互为相反数的两个数的积是14.如果a+b<0,ab>0,那么这两个数()A.都是正数B.都是负数C.一正一负D.符号无法确定5.如图所示,数轴上A,B两点所表示的两数的()A.和为正数B.和为负数C.积为正数D.积为负数6.在计算(112－78＋12)×(－48)时，可以避免通分的运算律是()A.加法交换律B.乘法交换律C.乘法分配律D.加法结合律7.下列运算过程有错误的个数是()①(3－412)×2=3－412×2②－4×(－7)×(－125)=－(4×125×7)③989×15=(10－19)×15=150－19×15④[3×(－25)]×(－2)=3×[(－25)×(－2)]=3×50A.1B.2C.3D.48.算式－25×14＋18×14－39×(－14)=(�

2022-2023年人教版数学九年级上册22.1.2《二次函数y＝ax2的图象和性质》课时练习一、选择题1.下列二次函数的图象中,开口最大的是()A.y=x2B.y=2x2C.y=110x2D.y=－x22.下列函数中，图象的最低点是原点的是()A.y=－3x2B.y=2x2C.y=2x＋1D.y=1x3.下列关于函数y=－12x2的图象说法：①图象是一条抛物线；②开口向下；③对称轴是y轴；④顶点坐标为(0,0).其中正确的有()A.1个B.2个C.3个D.4个4.下列各图象中有可能是函数y=ax2＋a(a≠0)的图象的是()5.已知二次函数y=x2和y=2x2，以下说法：①它们的图象都是开口向上；②它们的对称轴都是y轴，顶点坐标都是原点(0，0)；③当x>0时，它们的函数值y都是随着x的增大而增大；④它们开口的大小是一样的.其中正确的说法有()A.1个B.2个C.3个D.4个6.已知抛物线y=(m－1)x2经过点(－1，－2)，那么m的值是().A.1B.－1C.2D.－27.已知原点是抛物线y=(m+1)x2的最低点,�

《二次函数》全章复习与巩固—知识讲解（基础）【学习目标】1．通过对实际问题情境的分析确定二次函数的表达式，并体会二次函数的意义；2．会用描点法画出二次函数的图象，能从图象上认识二次函数的性质；3．会根据公式确定图象的顶点、开口方向和对称轴(公式不要求记忆和推导)，并能解决简单的实际问题；4．会利用二次函数的图象求一元二次方程的近似解.【知识网络】【要点梳理】要点一、二次函数的定义一般地，如果是常数，，那么叫做的二次函数.要点诠释：如果y=ax2+bx+c(a,b,c是常数，a≠0)，那么y叫做x的二次函数．这里，当a=0时就不是二次函数了，但b、c可分别为零，也可以同时都为零．a的绝对值越大，抛物线的开口越小.要点二、二次函数的图象与性质1.二次函数由特殊到一般，可分为以下几种形式：①；②；③；④，其中；�

幂的运算（提高）【学习目标】1.掌握正整数幂的乘法运算性质（同底数幂的乘法、幂的乘方、积的乘方）；2.能用代数式和文字语言正确地表述这些性质，并能运用它们熟练地进行运算.【要点梳理】【高清课堂396573幂的运算知识要点】要点一、同底数幂的乘法性质mnmnaaa(其中,mn都是正整数).即同底数幂相乘，底数不变，指数相加.要点诠释：（1）同底数幂是指底数相同的幂，底数可以是任意的实数，也可以是单项式、多项式.（2）三个或三个以上同底数幂相乘时，也具有这一性质，即mnpmnpaaaa（,,mnp都是正整数）.（3）逆用公式：把一个幂分解成两个或多个同底数幂的积，其中它们的底数与原来的底数相同，它们的指数之和等于原来的幂的指数。即mnmnaaa（,mn都是正整数）.要点二、幂的乘方法则()mnmnaa(其中,mn都是正整数).即

实际问题与一元一次方程（一）（基础）知识讲解【学习目标】1.熟练掌握分析解决实际问题的一般方法及步骤；2.熟悉行程，工程，配套及和差倍分问题的解题思路．【要点梳理】知识点一、用一元一次方程解决实际问题的一般步骤列方程解应用题的基本思路为：问题分析抽象方程求解检验解答．由此可得解决此类题的一般步骤为：审、设、列、解、检验、答．要点诠释：（1）“审”是指读懂题目，弄清题意，明确哪些是已知量，哪些是未知量，以及它们之间的关系，寻找等量关系；（2）“设”就是设未知数，一般求什么就设什么为x，但有时也可以间接设未知数；（3）“列”就是列方程，即列代数式表示相等关系中的各个量，列出方程，同时注意方程两边是同一类量，单位要统一；（4）“解”就是解方程，求出未知数的值�

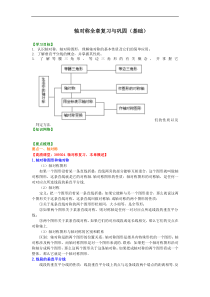
轴对称全章复习与巩固（基础）【学习目标】1.认识轴对称、轴对称图形，理解轴对称的基本性质及它们的简单应用；2.了解垂直平分线的概念，并掌握其性质；3.了解等腰三角形、等边三角形的有关概念，并掌握它们的性质以及判定方法.【知识网络】【要点梳理】要点一、轴对称【高清课堂：389304轴对称复习，本章概述】1.轴对称图形和轴对称（1）轴对称图形如果一个图形沿着某一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴.轴对称图形的性质：轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线.（2）轴对称定义：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴.成轴对称的两个图形的性质：①关于�

整式的乘法（提高）【学习目标】1.会进行单项式的乘法,单项式与多项式的乘法,多项式的乘法计算．2.掌握整式的加、减、乘、乘方的较简单的混合运算，并能灵活地运用运算律简化运算.【要点梳理】【高清课堂397531整式的乘法知识要点】要点一、单项式的乘法法则单项式与单项式相乘，把它们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它们的指数作为积的一个因式.要点诠释：（1）单项式的乘法法则的实质是乘法的交换律和同底数幂的乘法法则的综合应用.（2）单项式的乘法方法步骤：积的系数等于各系数的积，是把各单项式的系数交换到一起进行有理数的乘法计算，先确定符号，再计算绝对值；相同字母相乘，是同底数幂的乘法，按照“底数不变，指数相加”进行计算；只在一个单项式里含有的字母，要连同它�

2022-2023年人教版数学九年级上册22.1.2《二次函数y＝ax2的图象和性质》课时练习一、选择题1.下列二次函数的图象中,开口最大的是()A.y=x2B.y=2x2C.y=110x2D.y=－x2答案为：C.2.下列函数中，图象的最低点是原点的是()A.y=－3x2B.y=2x2C.y=2x＋1D.y=1x答案为：B.3.下列关于函数y=－12x2的图象说法：①图象是一条抛物线；②开口向下；③对称轴是y轴；④顶点坐标为(0,0).其中正确的有()A.1个B.2个C.3个D.4个答案为：D.4.下列各图象中有可能是函数y=ax2＋a(a≠0)的图象的是()答案为：B5.已知二次函数y=x2和y=2x2，以下说法：①它们的图象都是开口向上；②它们的对称轴都是y轴，顶点坐标都是原点(0，0)；③当x>0时，它们的函数值y都是随着x的增大而增大；④它们开口的大小是一样的.其中正确的说法有()A.1个B.2个C.3个D.4个答案为：C.6.已知抛物线y=(m－1)x2经过点(－1，－2)，那么m的值是(

2022-2023年人教版数学七年级上册1.4.1《有理数的乘法》课时练习一、选择题1.与－2的乘积为1的数是()A.2B.－2C.12D.－12答案为：D2.计算（﹣3）×3的结果是（）A.﹣9B.9C.0D.﹣6答案为：A3.下列说法错误的是()A.一个数同0相乘，仍得0B.一个数同1相乘，仍得原数C.一个数同－1相乘得原数的相反数D.互为相反数的两个数的积是1答案为：D4.如果a+b<0,ab>0,那么这两个数()A.都是正数B.都是负数C.一正一负D.符号无法确定答案为：B5.如图所示,数轴上A,B两点所表示的两数的()A.和为正数B.和为负数C.积为正数D.积为负数答案为：D6.在计算(112－78＋12)×(－48)时，可以避免通分的运算律是()A.加法交换律B.乘法交换律C.乘法分配律D.加法结合律答案为：C7.下列运算过程有错误的个数是()①×2=3-4×2②-4×(-7)×(-125)=-(4×125×7)③9×15=×15=150-④[3×(-25)]×(-2)=3×[(-25)×(-2)]=3×50A.1B.2C.3D.4答案为：A.8

实际问题与一元一次方程（二）（基础）知识讲解【学习目标】(1)进一步提高分析实际问题中数量关系的能力，能熟练找出相等关系并列出方程；(2)熟悉利润，存贷款，数字及方案设计问题的解题思路．【要点梳理】要点一、用一元一次方程解决实际问题的一般步骤列方程解应用题的基本思路为：问题分析抽象方程求解检验解答．由此可得解决此类问题的一般步骤为：审、设、列、解、检验、答．要点诠释：（1）“审”是指读懂题目，弄清题意，明确哪些是已知量，哪些是未知量，以及它们之间的关系，寻找等量关系．（2）“设”就是设未知数，一般求什么就设什么为x，但有时也可以间接设未知数．（3）“列”就是列方程，即列代数式表示相等关系中的各个量，列出方程，同时注意方程两边是同一类量，单位要统一．（4）�

图形的旋转--知识讲解【学习目标】1、掌握旋转的概念，探索它的基本性质，理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质；2、能够按要求作出简单平面图形旋转后的图形，并能利用旋转进行简单的图案设计.【要点梳理】要点一、旋转的概念把一个图形绕着某一点O转动一个角度的图形变换叫做旋转..点O叫做旋转中心，转动的角叫做旋转角(如∠AOA′),如果图形上的点A经过旋转变为点A′，那么，这两个点叫做这个旋转的对应点.要点诠释：旋转的三个要素：旋转中心、旋转方向和旋转角度.要点二、旋转的性质(1)对应点到旋转中心的距离相等（OA=OA′）；(2)对应点与旋转中心所连线段的夹角等于旋转角；(3)旋转前、后的图形全等(△ABC≌△ABC).要点诠释：图形绕某一点旋转，既可以按顺时针旋转也可以按逆�

幂的运算（基础）【学习目标】1.掌握正整数幂的乘法运算性质（同底数幂的乘法、幂的乘方、积的乘方）；2.能用代数式和文字语言正确地表述这些性质，并能运用它们熟练地进行运算.【要点梳理】【高清课堂396573幂的运算知识要点】要点一、同底数幂的乘法性质mnmnaaa(其中,mn都是正整数).即同底数幂相乘，底数不变，指数相加.要点诠释：（1）同底数幂是指底数相同的幂，底数可以是任意的实数，也可以是单项式、多项式.（2）三个或三个以上同底数幂相乘时，也具有这一性质，即mnpmnpaaaa（,,mnp都是正整数）.（3）逆用公式：把一个幂分解成两个或多个同底数幂的积，其中它们的底数与原来的底数相同，它们的指数之和等于原来的幂的指数。即mnmnaaa（,mn都是正整数）.要点二、幂的乘方法则()mnmnaa(其中,mn都是正整数).即

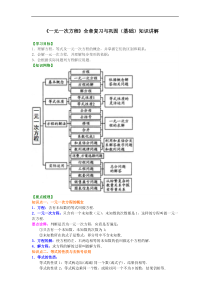
《一元一次方程》全章复习与巩固（基础）知识讲解【学习目标】1．理解方程，等式及一元一次方程的概念，并掌握它们的区别和联系；2．会解一元一次方程，并理解每步变形的依据；3．会根据实际问题列方程解应用题．【知识网络】【要点梳理】知识点一、一元一次方程的概念1．方程：含有未知数的等式叫做方程．2．一元一次方程：只含有一个未知数（元），未知数的次数都是1，这样的方程叫做一元一次方程．要点诠释：判断是否为一元一次方程，应看是否满足：①只含有一个未知数，未知数的次数为1；②未知数所在的式子是整式，即分母中不含未知数．3．方程的解：使方程的左、右两边相等的未知数的值叫做这个方程的解．4．解方程：求方程的解的过程叫做解方程．知识点二、等式的性质与去括号法则1．等式的性质：等式的性质1：�

2022-2023年人教版数学九年级上册22.1.3《二次函数y=a(x－h)2＋k的图象和性质》课时练习一、选择题1.抛物线y=2(x+3)2+1的顶点坐标是()A.(3，1)B.(3，﹣1)C.(﹣3，1)D.(﹣3，﹣1)2.抛物线y=(x－2)2+3的顶点坐标是().A.(2，3)B.(－2，3)C.(2，－3)D.(－2，－3)3.图象的顶点为(﹣2，﹣2)，且经过原点的二次函数的关系式是()A.y=12(x+2)2﹣2B.y=12(x﹣2)2﹣2C.y=2(x+2)2﹣2D.y=2(x﹣2)2﹣24.二次函数y=(x﹣1)2+2的最小值是()A.2B.1C.﹣1D.﹣25.将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式，结果为()A.y=(x+1)2+4B.y=(x+1)2+2C.y=(x﹣1)2+4D.y=(x﹣1)2+26.对于一般的二次函数y=x2+bx+c，经过配方可化为y=(x﹣1)2+2，则b，c的值分别为()A.5，﹣1B.2，3C.﹣2，3D.﹣2，﹣37.若抛物线的顶点坐标是(﹣2，1)且经过点(1，﹣8)，则该抛物线的表达式是()A.y=﹣9(x﹣2)2+1B.y=﹣7(x﹣2)2﹣1C.y=﹣(x+2)2+1D.y=﹣79(x+2)2﹣18.已知二次函数y＝3(x﹣1)2＋k的图�

中心对称与中心对称图形--知识讲解【学习目标】1、理解中心对称和中心对称图形的定义和性质，掌握他们之间的区别和联系；2、掌握关于原点对称的点的坐标特征，以及如何求对称点的坐标；3、探索图形之间的变化关系（轴对称、平移、旋转及其组合），灵活运用轴对称、平移和旋转的组合进行图案设计．【要点梳理】要点一、中心对称和中心对称图形1.中心对称：把一个图形绕着某一个点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心．这两个图形中的对应点叫做关于中心的对称点．要点诠释：（1）有两个图形，能够完全重合，即形状大小都相同；（2）位置必须满足一个条件：将其中一个图形绕着某一个点旋转180°能够与另一个图形重合(全等图形不一定是中心对称的，而中�

乘法公式（提高）【学习目标】1.掌握平方差公式、完全平方公式的结构特征，并能从广义上理解公式中字母的含义；2.学会运用平方差公式、完全平方公式进行计算.了解公式的几何意义，能利用公式进行乘法运算；3.能灵活地运用运算律与乘法公式简化运算.【要点梳理】【高清课堂乘法公式知识要点】要点一、平方差公式平方差公式：22()()ababab两个数的和与这两个数的差的积，等于这两个数的平方差.要点诠释：在这里，ba,既可以是具体数字，也可以是单项式或多项式.抓住公式的几个变形形式利于理解公式.但是关键仍然是把握平方差公式的典型特征：既有相同项，又有“相反项”，而结果是“相同项”的平方减去“相反项”的平方.常见的变式有以下类型：（1）位置变化：如()()abba利用加法交换律可以转化为公式的标准型（2）系

2022-2023年人教版数学七年级上册1.4.2《有理数的除法》课时练习一、选择题1.计算6÷(﹣3)的结果是()A.﹣12B.﹣2C.﹣3D.﹣182.计算：3÷(﹣1)的结果是()A.﹣3B.﹣2C.2D.33.下列说法不正确的是()A.一个不为0的数与它的倒数之积是1B.一个不为0的数与它的相反数的商是1C.两个数的商为－1，这两个数互为相反数D.两个数的积为1，这两个数互为倒数4.两个因数相乘，其中一个因数是35，积是－1，那么另一个因数是()A.35B.53C.－35D.－535.在算式4－|－3□5|中的□所在位置，填入下列哪种运算符号，计算出来的值最小()A.＋B.－C.×D.÷6.小华作业本中有四道计算题：①0﹣(﹣5)=﹣5；②(﹣3)+(﹣9)=﹣12；③23×(﹣94)=﹣32④；(﹣36)÷(﹣9)=﹣4.其中他做对的题的个数是()A.1个B.2个C.3个D.4个7.下列四个算式中，误用分配律的是()A.12×(2－13＋16)=12×2－12×13＋12×16B.(2－13＋16)×12=2×12－13×12＋16×