【文档说明】人教版七年级数学上册17《一元一次方程 全章复习与巩固》知识讲解+巩固练习(基础版)（含答案）.doc，共(8)页，239.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-24052.html

以下为本文档部分文字说明：

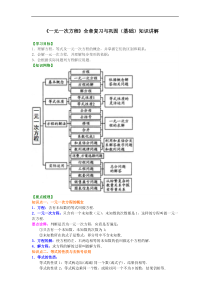
《一元一次方程》全章复习与巩固（基础）知识讲解【学习目标】1．理解方程，等式及一元一次方程的概念，并掌握它们的区别和联系；2．会解一元一次方程，并理解每步变形的依据；3．会根据实际问题列方程解应用题．【知识网络】【要点梳理】

知识点一、一元一次方程的概念1．方程：含有未知数的等式叫做方程．2．一元一次方程：只含有一个未知数（元），未知数的次数都是1，这样的方程叫做一元一次方程．要点诠释：判断是否为一元一次方程，应看是否满足：①

只含有一个未知数，未知数的次数为1；②未知数所在的式子是整式，即分母中不含未知数．3．方程的解：使方程的左、右两边相等的未知数的值叫做这个方程的解．4．解方程：求方程的解的过程叫做解方程．知识点二、等式的性质与去括号法则1．等式的性质：等式的性质1：等式两边加(或减)同一个数(或式

子)，结果仍相等．等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等．2．合并法则：合并时，把系数相加(减)作为结果的系数，字母和字母的指数保持不变．3．去括号法则：（1）括号外的因数是正数，去括号后各项的符号与原括号内相应各

项的符号相同．（2）括号外的因数是负数，去括号后各项的符号与原括号内相应各项的符号相反．知识点三、一元一次方程的解法解一元一次方程的一般步骤：(1)去分母：在方程两边同乘以各分母的最小公倍数．(2)去括号：依据乘法分配律和去括号法则，先去小括号，再去中括号，最

后去大括号．(3)移项：把含有未知数的项移到方程一边，常数项移到方程另一边．(4)合并：逆用乘法分配律，分别合并含有未知数的项及常数项，把方程化为ax＝b(a≠0)的形式．(5)系数化为1：方程两边同除以未知数的系数得到方程的解bxa(a≠0)．

(6)检验：把方程的解代入原方程，若方程左右两边的值相等，则是方程的解；若方程左右两边的值不相等，则不是方程的解．知识点四、用一元一次方程解决实际问题的常见类型1.行程问题：路程＝速度×时间2.和差倍分问题：增长量＝原有量×增长率3.利润问题：商品

利润＝商品售价－商品进价4.工程问题：工作量＝工作效率×工作时间，各部分劳动量之和＝总量5.银行存贷款问题：本息和＝本金+利息，利息＝本金×利率×期数6.数字问题：多位数的表示方法：例如：32101010abcdabcd.【典型例题】类型一、一元一次方程的概念1．（2

016春•南江县期末）在下列方程中①x2+2x=1，②﹣3x=9，③x=0，④3﹣=2，⑤=y+是一元一次方程的有（）个．A．1B．2C．3D．4【思路点拨】若一个整式方程经过化简变形后，只含有一个未知数，并且未知数的次数都是1，系数不为0，则这个方程是一元一次方程．【答案与解析】解：①x2

+2x=1，最高次数是2次；②﹣3x=9，分母上含有字母，不是整式方程；③x=0，是一元一次方程；④3﹣=2，是一个等式，不是方程；⑤=y+是一元一次方程；一元一次方程的有2个，故选：B．【总结升华】本题考查了一元一次

方程的定义，解决本题的关键是熟记一元一次方程的定义．凡是分母中含有未知数的方程一定不是一元一次方程．举一反三：【高清课堂：一元一次方程复习393349等式和方程例(1)】【变式】下列说法中正确的是().A．2a-a=a不是等式B．x2-2x-3是方程

C．方程是等式D．等式是方程【答案】C2.若方程3(x-1)+8＝2x+3与方程253xkx的解相同，求k的值．【答案与解析】解：解方程3(x-1)+8＝2x+3，得x＝-2．将x＝-2代入方程253xkx中，得22253k．解这个

关于k的方程，得263k．所以，k的值是263k．【总结升华】由于两个方程的解相同，所以可以将其中一个方程的解代入另一个方程中，从而求得问题的答案．举一反三：【变式】（2015春•泉州期中）当x=

时，代数式2x+1与5x﹣8的值相等．【答案】3．解：根据题意得：2x+1=5x﹣8，∴2x﹣5x=﹣8﹣1，∴﹣3x=﹣9，∴x=3.类型二、一元一次方程的解法3．解方程235146yy【思路点拨】通过方程的同解原理(去分母，去括号，合并同类项，系数化为1)，一步一步将一个复杂的方

程转化成与它同解的最简的方程，从而达到求解的目的．【答案与解析】解：去分母，得3(y+2)-2(3-5y)＝12去括号，得3y+6-6+10y＝12合并同类项，得13y＝12未知数的系数化为1，得1213y【总结升华

】转化思想是初中数学中一种常见的思想方法，它能将复杂的问题转化为简单的问题，将生疏的问题转化为熟悉的问题，将未知转化为已知．事实上解一元一次方程就是利用方程的同解原理，将复杂的方程转化为简单的方程直至求出它的解．4．解方程：113(1)(1)2(1

)(1)22xxxx【思路点拨】本题按常规方法求解，比较繁锁，如能根据题目的特点，巧用“整体思维”，就能算得又快又对，起到事半功倍的效果．【答案与解析】解：113(1)(1)2(1)(1)22xxxx75(1)(1)22xx7(1)5(1)xx7

755xx212xx＝-6【总结升华】直接去括号太繁琐，若将(x+1)及(x-1)看作一个整体，并移项合并同类项，解答十分巧妙，可免去去分母的步骤及简化去括号的过程．举一反三：【变式】解方程：278(x-4)-463(8-2x)-888(7x-28)

＝0【答案】解：原方程可化为278(x-4)+463×2(x-4)-888×7(x-4)＝0(x-4)(278+463×2-888×7)＝0x-4＝0x＝4类型三、一元一次方程的应用5.甲车从A地出发以60km／h的速度沿公路匀速行驶，0.5h后，乙车也从A地出发，以80km／h的速度沿

该公路与甲车同向匀速行驶，求乙车出发后几小时追上甲车．【答案与解析】解：设乙车出发后x小时追上甲车，依题意得60×0.5+60x＝80x，解得x＝1.5．答：乙车出发后1.5小时追上甲车．【总结升华】此题

的等量关系为：甲前0.5h的行程+甲后来的行程＝乙的行程．6.（2015•东城区一模）列方程或方程组解应用题：2015年“植树节”前夕，某小区为绿化环境，购进200棵柏树苗和120棵枣树苗，且两种树苗所需费用相同．每棵枣树苗的进价比每棵

柏树苗的进价的2倍少5元，每棵柏树苗的进价是多少元？【答案与解析】解：设每棵柏树苗的进价是x元，则每棵枣树苗的进价是（2x﹣5）元，根据题意，列方程得：200x=120（2x﹣5），解得：x=15．答：每棵柏树苗的进价是15元．【总结升华】此题考查了一元一次方程

的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．举一反三：【高清课堂：一元一次方程复习393349一元一次方程的解法和应用例6】【变式】某文具店为促销X型计算器，优惠条件是一次购买不超过10个，每个38元，超过10个，超

过部分每个让利2元(即每个36元)，问李老师用812元共买了多少个？【答案】解：设李老师用812元共买了x个，依题意可得：381036(10)812x解得：22x答：李老师用812元共买了22个．【巩固练习】一、选择题1．下列方程中，是一元一次方程的是()．A．250xB．42xy

C．162xD．x＝02.下列变形错误的是()A.由x+7=5得x+7－7=5－7;B.由3x－2=2x+1得x=3C.由4－3x=4x－3得4+3=4x+3xD.由－2x=3得x=－323.某书中一道方程题

：213xx，□处在印刷时被墨盖住了，查书后面的答案，得知这个方程的解是2.5x，那么□处应该是数字()．A．-2.5B．2.5C．5D．74.将(3x＋2)－2(2x－1)去括号正确的是()A3x＋2－2x＋1B3x＋2－4x＋1C3x＋2－4x－2D3x＋2－4x＋2

5.当x=2时，代数式ax－2x的值为4，当x=－2时，这个代数式的值为（）A.－8B.－4C.－2D.86．（2016•株洲）在解方程时，方程两边同时乘以6，去分母后，正确的是（）A．2x﹣1+6x=3（3x+1）B．2（x﹣1）+6x

=3（3x+1）C．2（x﹣1）+x=3（3x+1）D．（x﹣1）+x=3（x+1）7．某球队参加比赛，开局11场保持不败，积23分，按比赛规则，胜一场得3分，平一场得1分，则该队获胜的场数为()．A．4

B．5C．6D．78.（2015•河北模拟）某单位元旦期间组织员工到正定出游，原计划租用28座客车若干辆，但有4人没有座位，若租用同样数量的33座客车，只有一辆空余了11个座位，其余客车都已坐满，则该单位组织出游的员工有（）A．80人B．84人C．88人D．92人二、填空题9．在

0，－1，3中，是方程3x－9=0的解.10．如果3x52a＝－6是关于x的一元一次方程，那么a＝，方程的解x.11.（2015•苏州一模）若关于x的方程2x+a=5的解为x=﹣1，则a=7．12．由3x＝2x＋1变为3x－2x

＝1，是方程两边同时加上.13．“代数式9－x的值比代数式x32－1的值小6”用方程表示为.14．当x＝时，代数式223x与32x互为相反数.15．有两桶水，甲桶水装有180升，乙桶装有150升，要使两桶水的重量相同，则甲桶应向乙桶倒水升.16．某商场把彩电按标价的8折

出售，仍可获利20%，若该彩电的进价为2000元，则标价是.三、解答题17．（1）310.10.3542xx；（2）122(1)(3)23xxx．18．已知代数式11213yy的值为0，求代数式312143yy

的值．19.（2016•黄冈）在红城中学举行的“我爱祖国”征文活动中，七年级和八年级共收到征文118篇，且七年级收到的征文篇数是八年级收到的征文篇数的一半还少2篇，求七年级收到的征文有多少篇？20．学校

校办工厂需制作一块广告牌，请来师徒二人，已知师傅单独完成需4天，徒弟单独完成需6天，现由徒弟先做一天，再两人合作，完成后共得到报酬450元，如果按各人完成的工作量计算报酬，那么该如何分配?【答案与解析】一、选择题1.【答案】D2.【答案】D【解析】由23x，得32x3.【答案】C【解

析】把x＝-2.5代入方程，再把□当作未知数解方程即可．4.【答案】D【解析】(32)2(21)32222(1)3242xxxxxx5．【答案】B【解析】将2x代入得：244a，得28a；将2x代入得：24844a6．【答案】B【解析】解：方程

两边同时乘以6得：2（x﹣1）+6x=3（3x+1），故选B．7．【答案】C【解析】设该队获胜x场，则平的场数为(11-x)，则3x+(11-x)＝23．解得x＝6．故选C．8.【答案】C.【解析】设租用28座客车x辆．则28x+4=33x﹣11，解得x=3，则28x+4=28

×3+4=88（人），即该单位组织出游的员工有88人．二、填空题9.【答案】3；【解析】代入验证即可．10.【答案】35，-2；【解析】35215aa，362xx11.【答案】7.【解析】把x=﹣1代入方程2x+a=

5，得：﹣2+a=5，解得：a=7．12.【答案】-2x；13.【答案】29)613xx（；14.【答案】138；【解析】322023xx，解得：138x15.【答案】15；【解析】设倒x升，得：

180150xx，解得：15x16.【答案】3000.【解析】设标价为x元，则0.82000(120%)x,解得：3000x三、解答题17．【解析】解：(1)去分母，得3x-0.4＝2x+1.4．移项，得3x-2x＝1.4+0.4．合并同类项，得x＝1.8．(2)去

分母，得12x-3(x-1)＝4(x+3)．去括号，得12x-3x+3＝4x+12．移项，得12x-3x-4x＝12-3．合并同类项．得5x＝9．系数化为1，得95x．18．【解析】解：由题意，得112103yy

．去分母，得61130yy．移项合并同类项，得714y．系数化为1，得y＝2．当y＝2时，3121321221143434yy，即若代数式11213yy的值为0，则代数式312143yy的值为14．19.【解析】解：设七年级收到的征文有

x篇，则八年级收到的征文有（118﹣x）篇，依题意得：（x+2）×2=118﹣x，解得：x=38．答：七年级收到的征文有38篇．20．【解析】解：设两人一起做x天，据题意，得：11(1)164xx，解得

x＝2．师傅应得报酬为14×2×450＝225(元)．徒弟应得报酬为450-225＝225(元)．答：师傅应得报酬为225元，徒弟应得报酬为225元．