【文档说明】人教版高中数学选择性必修第二册专题5.4《一元函数的导数及其应用》单元测试卷提升卷(解析版).doc，共(15)页，904.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38107.html

以下为本文档部分文字说明：

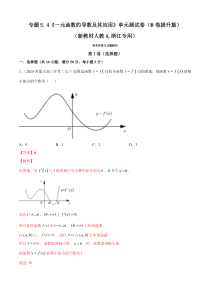
专题5.4《一元函数的导数及其应用》单元测试卷（B卷提升篇）（新教材人教A,浙江专用）参考答案与试题解析第Ⅰ卷（选择题）一．选择题（共10小题，满分50分，每小题5分）1．（2020·内蒙古高三月考（文））如图是函数yfx的导函数

yfx的图象，则函数yfx的极小值点的个数为（）A．0B．1C．2D．3【答案】B【解析】由图象，设fx与x轴的两个交点横坐标分别为a、b其中ab，知在(,)a，(,)b上()0fx，所以此时函数()fx在(,)a，(,)b上单调递增，在(,)ab上，(

)0fx，此时()fx在(,)ab上单调递减，所以xa时，函数取得极大值，xb时，函数取得极小值．则函数()yfx的极小值点的个数为1．故选:B2．（2020·湖南长郡中学高二期中）若函数

fx，gx满足21fxxgxx，且11f，则11fg（）A．1B．2C．3D．4【答案】C【解析】因为函数fx，gx满足21fxxgxx，且11f，所以211110f

g，则11g，对21fxxgxx两边求导，可得2fxgxxgxx，所以1112fgg，因此113fg.故选：C.3.（2020·安徽淮北一中高二期中）等比数列

{}na中，12a，84a，函数128()()()()fxxxaxaxa…，则(0)(f（）A．26B．29C．212D．215【答案】C【解析】等比数列{}na中，12a，84a，所以18

273645248aaaaaaaa，因为函数128()()()()fxxxaxaxa，128128()()()()()()()fxxaxaxaxxaxaxa，则441211882

(0)()82faaaaa．故选：C．4．（2020·天津经济技术开发区第二中学高三期中）函数3()1216fxxx的零点个数为（）A．0B．1C．2D．3【答案】C【解析】由题得2()3123(2)(2)f

xxxx，令()0fx得2x或2x，令()0fx得22x，所以函数的单调递增区间为(,2),(2,)，减区间为(2,2).所以函数的极大值为(2)0f，极

小值为(2)32f，当x时，0,y当x时，0,y所以函数的零点个数为2.故选：C5.（2020·辽宁高三月考）点P是曲线2lnyxx上任意一点，曲线在点P处的切线与1yx平

行，则P的横坐标为（）A．1B．2C．22D．22【答案】A【解析】由题意，设00,Pxy，00x，由2lnyxx得12yxx，则00012xxyxx，因为曲线在点P处的切线与1yx平行，所以00121xx，解得：01x或012x（舍）故选

：A.6．（2020·宁夏银川一中高三月考（文））若函数22lnfxxxax在0,1上单调递减，则实数a的取值范围是（）A．4aB．4aC．4aD．4a【答案】C【解析】由题意可得：220afxxx在0,1上恒成立，整理可得：22

2axx，函数222yxx在0,1上递减，所以(4,0)y，所以4a，故选：C.7．（2020·湖北高三月考）若函数2sincosfxaxaxx是R上的增函数，则实数a的取值范围是（）A．3,3B．3,3

C．,3D．3,【答案】B【解析】因为2sincosfxaxaxx，所以2()2cossin1sin()2,tanfxaaxxaxaa因为()fx在R

上的增函数，所以()0fx在R上恒成立，所以2min()120fxaa，即221aa，所以22041aaa，解得33a，故选：B8．（2020·全国高三专题练习（理））已知函数()xbfx

eax,abR，且(0)1f，当0x时，()cos(1)fxxx恒成立，则a的取值范围为（）A．(0,)B．(1,)eC．(,)eD．(,)e【答案】B【解析】由题意，(0)1bfe，解得0b

，则()xfxeax，则当0x时，cos(1)xeaxxx，即cos(1)xeaxx恒成立，令(),(0,)xesxxx，则2(1)()xexsxx，当(0,1)x时，()0sx，(1,)x时，()0sx

，所以()sx在(0,1)上是减函数，在(1,)是增函数，min()(1)sxse，又因为当1x时，cos(1)x取得最大值1，所以当1x时，cos(1)xexx取得最大值1e，所以1ae.故选：B.9

．（2020·江西高三其他模拟（理））设函数1xfxeaxb在区间0,1上存在零点，则22ab的最小值为（）A．7B．eC．2eD．3e【答案】C【解析】由题意，函数1xfxeaxb，设

t为函数fx在0,1上的零点，则10teatb，即10ttabe，即点(,)ab在直线10ttxye上，又由22ab表示点(,)ab到原点的距离的平方，则222

2(1)1tabet，即22222(1)1teabt，令222(1)1tegtt，则2222222222(22)(22)2(33)(22)(22)tttettetettgttttt

，因为220,330tett，所以0gt，可得函数gt在区间0,1t上单调递增，所以当1t时，函数取得最大值，最大值为21ge，所以22ab的最小值为2e.故选：C.10．（2020·浙江绍兴·高三月考）已知e为自然对数的底数，,ab为实

数，且不等式ln(21)10xeaxb对任意的(0,)x恒成立.则当21ba取最大值时，a的值为（）A．2eB．21eC．3eD．31e【答案】D【解析】设ln(21)1fxxeaxb，则121fxeax，当21ae时

，0fx，所以fx在0,上递增，不符合条件，故21ae，令0fx得112xae，所以fx在10,12ae上递增，1,12ae上递增，故有max11ln01212fxfbaeae

，即ln12bae，则有ln122211aebaa，令1,2tate，ln22tegtt，则ln222ttetegtt在2,e上递减，且30ge，所以gt在2,3ee上递增，

3,e上递减，所以3gtge，此时21ba取得最大值，且13ae，所以31ae.故选：D第Ⅱ卷（非选择题）二．填空题（共7小题，单空每小题4分，两空每小题6分，共36分）11．（2020·湖北高三月考）

函数lnfxxx，在点,Pee处的切线方程为__________.【答案】2yxe【解析】()lnfeeee()ln1fxx，()ln12fee在点,Pee处的切线方程为2()yexe

，即2yxe故答案为：2yxe12．（2020·全国高二课时练习）某批发商以每吨20元的价格购进一批建筑材料，若以每吨M元零售，销量N（单位：吨）与零售价M（单位：元）有如下关系：28300170NMM，则

该批材料零售价定为_______元时利润最大，利润的最大值为_________元.【答案】3023000【解析】设该商品的利润为y元，由题意知，32(20)15011700166000yNMMMM，则2330011700yMM，令0

y，得30M或130M（舍去），当(0,30)M时，0y，当(30,)M时，0y，因此当30M时，y取得极大值，也是最大值，且max23000y.故答案为：30，2300013．（2020·天津经济技术开发区第二中学高三期中）已知函数3

2()245fxaxxx，当23x时，函数()fx有极值，则函数()fx在3,1上的最大值为_________.【答案】13【解析】2344fxaxx，当23x时，函数()fx有极值，2440333fa，解得1a，234432

2fxxxxx，当3,2x时，0fx，fx单调递增，当22,3x时，0fx，fx单调递减，当2,13x时，0fx，fx单调递增，fx在2x处取得极大值213f，且3

8f，14f，()fx在3,1上的最大值为13.故答案为：13.14．（2020·全国高三专题练习）已知函数ln1xfxaex，设x=1是fx的极值点，则a=___，fx的单调增区

间为___.【答案】1e1,【解析】由题意可得：1xfxaex1x是fx的极值点110fae1ae即1ln1xfxex11xfxex令0fx，可得1xfx的单调递增区

间为1,15.（2020·全国高二单元测试）已知函数2ln(1)fxaxx，对任意的(0,1),(0,1)pq，当pq时，(1)(1)1fpfqpq，则实数a的取值范围是________．【答案】[15,).【解析】由题意，分式(1)(1)fpfqp

q的几何意义为：表示点(1,(1))pfp与(1,(1))qfq连线的斜率，因为实数,pq在区间(0,1)内，故1p和1q在区间(1,2)内，不等式(1)(1)1fpfqpq恒成立，

所以函数图象上在区间(1,2)内任意两点连线的斜率大于1，故函数2ln(1)fxaxx的导数大于1在(1,2)内恒成立，由函数2ln(1)fxaxx满足10x，即定义域为(1,)，即211afxxx在(1,2)内恒成

立，即2231axx在(1,2)内恒成立，设函数2231gxxx，根据二次函数的性质，可得函数2231gxxx在(1,2)上是单调增函数，可得215gxg，所以15a，即实数a的取值范围是[15,).16．（2020·辽宁高三月考）已知函数22ln

fxaxxx有两个不同的极值点1x，2x，则a的取值范围___________；且不等式1212fxfxxxt恒成立，则实数t的取值范围___________.【答案】10,25,【解析】2221()(0)axxfxxx，因为函数22

lnfxaxxx有两个不同的极值点12,xx,所以方程22210axx有两个不相等的正实数根，于是有：121248010102axxaxxa，解得102a.221112221212122ln2lnfxfxxxxa

xxxaxxxx212121212()23lnaxxxxxxxx21ln2aa,设21()1ln2,02haaaa,22()0ahaa，故()ha在102a上单调递增，故1()52hah

，所以5t.因此t的取值范围是5,故答案为：10,2；5,17．（2020·湖北荆州市·高二期末）已知函数1()ln(0)fxaxxax．（1）当1a时，()fx的极小值为________；（2）若()fxax在(0,)上恒

成立，则实数a的取值范围为___________．【答案】120,e【解析】（1）1a时，1()fxxlnxx，(0)x，21()1fxlnxx，312()0fxxx，故()fx在

(0,)单调递增，而f（1）0，故(0,1)x时，()0fx，()fx单调递减，(1,)x时，()0fx，()fx单调递增，故()fx极小值f（1）1；（2）若()fxax…在(0,

)上恒成立，即21(1)alnxx„在(0,)恒成立，①10lnx„即xe…时，0a，(1)0lnx„，210x，故21(1)alnxx„在(0,)恒成立，②10lnx即0xe时，即为21

(1)axlnx„在(0,)恒成立，即21[](1)minaxlnx„，只需求出2()(1)gxxlnx的最大值即可，(0)xe，()(12)gxxlnx，令()0gx，解得：0xe，令()0gx，解得：exe，故()gx在(0,)e单调递增，在(e，

)e单调递减，故()()2maxegxge，故122aee„，综上，(0a，2]e．故答案为：1，(0，2]e．三．解答题（共5小题，满分64分，18--20每小题12分，21,22每小题14分）18．（2020·南通

西藏民族中学高二期中）已知函数f(x)＝x＋4x，g(x)＝2x＋a.（1）求函数f(x)＝x＋4x在1,12上的值域；（2）若∀x1∈1,12，∃x2∈[2，3]，使得f(x1)≥g(x2)，

求实数a的取值范围.【答案】（1）[5,17]2；（2）1a.【解析】（1）222441xfxxx，因为1,12x，所以0fx，即函数fx为减函数，因为51217,12ff，所以值域为[5,17]2.（

2）因为∀x1∈1,12，∃x2∈[2，3]，使得f(x1)≥g(x2)，所以12minminfxgx，因为2[2,3]x，所以2224agxa，所以54a，即1a.19.（2020·甘肃省岷

县第一中学高二开学考试（理））已知函数32391fxxxxxR．（1）求函数fx的单调区间．（2）若210fxa对2,4x恒成立，求实数a的取值范围.【答案】（1）单调增区间(,1),(3,)单调减区间1,3（2）252a

【解析】（1）令，解得或，令，解得：.故函数的单调增区间为，单调减区间为.（2）由（1）知在上单调递增，在上单调递减，在上单调递增，又，，，∴，∵对恒成立，∴，即，∴20．（2020·南昌县莲塘第三中学高

二期末（理））已知函数2()2lnfxxx.(Ⅰ)求函数()fx的单调区间；(Ⅱ)求证：当2x时，()34fxx.【答案】(1)f(x)的单调增区间为(1，＋∞),单调减区间为(0，1)；(2)见解析.【解析】(1)依题意知函数的定义域为{x|x>0}，∵f′(x)＝

2x-2=2(1)(1)xxx，由f′(x)>0，得x>1;由f′(x)<0，得0<x<1∴f(x)的单调增区间为(1，＋∞),单调减区间为(0，1)．(2)设g(x)＝f（x）-3x+1=x2－2lnx-3x+4，∴g′(x)＝2x-2--3=2232

(21)(2)xxxxxx，∵当x>2时，g′(x)>0，∴g(x)在(2，＋∞)上为增函数，∴g(x)>g(2)＝4-2ln2-6+4>0，∴当x>2时，x2-2lnx>3x-4,即当x>2时()34fxx..21.（2020·江西景德镇一中高二期中）已知函数2

()ln(2)fxxaxax.（1）求函数()fx的单调区间；（2）若对任意0,x，函数()fx的图象不在x轴上方，求实数a的取值范围.【答案】（1）详见解析；（2）[1,).【解析】（1）函数2()ln(2)fxxaxax定义域为0,，则

(2)1211()2(2)axxfxaxaxx，当20a时，()0fx，()fx递增，当20a时，令()0fx，解得102xa，令()0fx，解得12

xa，所以()fx在10,2a递增，在1,2a递减；（2）若对任意0,x，函数()fx的图象不在x轴上方，则2()ln(2)0fxxaxax，0,x恒成立，则22ln2xxax

x，0,x恒成立，令22ln2xxgxxx，则22211lnxxxgxxx，令1lnhxxx，则110hxx，所以hx在0,递减，而10h，所以当

01x时，0gx，当1x时，0gx，所以当1x时，gx取得最大值1，所以1a，所以实数a的取值范围是[1,).22．（2020·四川省阆中东风中学校高三月考（文））已知函数2ln21fxxaxax，其中a为常数，且0a

.（1）当2a时，求fx的单调区间；（2）若fx在1x处取得极值，且在0,e的最大值为1，求a的值.【答案】（1）在10,4和1,上单调递增，在1,14上单调递减；（2）

12ae或2a.【解析】（1）2ln25fxxxx，411145xxfxxxx，令0fx，得14x或1，则列表如下：x10,4141,1411,

fx+0_0+fx增极大值减极小值增所以fx在10,4和1,上单调递增，在1,14上单调递减.（2）∵211axxxfx，令0fx，11x，212xa，因为fx在1x处取得极值，所以21112xxa

，①102a时，fx在0,1上单调递增，在1,e上单调递减，所以fx在区间1,e上的最大值为1f，令11f，解得2a；②当0a，2102xa；(i)当112a时，fx在10,2a上单调递增，1,12a上单

调递减，1,e上单调递增，所以最大值1可能在12xa或xe处取得，而2111111ln21ln10222224faaaaaaaa，∴2ln211feeaeae，∴12ae，(

ii)当112ea时，fx在区间0,1上单调递增；11,2a上单调递减，1,2ea上单调递增，所以最大值1可能在1x或xe处取得而1ln1210faa，所以2ln211f

eeaeae，解得12ae，与2112xea矛盾；(iii)当21e2xa时，fx在区间0,1上单调递增，在1,e单调递减，所以最大值1可能在1x处取得，而1ln1210faa，矛盾，综上所述，12ae或2a.