【文档说明】2021年高中数学人教版必修第一册：3.1《函数的概念及表示》精品讲义(含解析).doc，共(17)页，1.021 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31216.html

以下为本文档部分文字说明：

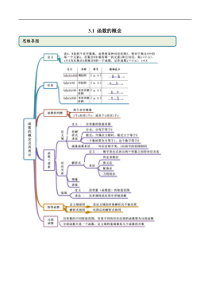
3.1函数的概念思维导图考点一区间的表示【例1】（2019·全国高一）一般区间的表示设,abR，且ab，规定如下:定义名称符号数轴表示{|}xaxb闭区间______{|}xaxb开区间______{|}xaxb半开半闭区间______{|}xaxb半开半闭区间__

____【答案】,ab,ab,ab,ab【解析】(1).若{|}xaxb,写成区间形式为,ab常见考法(2).若{|}xaxb,写成区间形式为,ab(3).若{|}xaxb,写成区间形

式为,ab(4).若{|}xaxb,写成区间形式为,ab故答案为:(1).,ab(2).,ab(3).,ab(4).,ab【一隅三反】1．（2019·全国高一课时练习）已知区间41,21pp，则p的取值范围为__

____．【答案】,1【解析】由题意，区间41,21pp，则满足4121pp，解得1p，即p的取值范围为,1．故答案为,1．2．（2019·全国高一课时练习）用区间表示下列集合：（1）1xx______；（2）201xxx

______；（3）128xxx或______．【答案】1,,12,12,8【解析】（1）根据集合与区间的改写，可得11,xx．（2）由20{11xxxxx

或2}=,12,x．（3）由{|1xx或28}=128x，．3．（2019·全国高一课时练习）用区间表示下列集合：1xx______；25xx______；

3xx______；24xx______.【答案】1,2,5,32,4【解析】集合1xx表示大于1的所有实数，可用开区间表示为1,；集合25xx表示大不等式改写成区间表达形式,注意边界情况于2且

小于或等于5的所有实数，可用左开右闭区间表示为2,5；集合3xx表示小于或等于3的所有实数，可用左开右闭区间表示为,3；集合24xx表示大于或等于2且小于或等于4的所有实数，可用闭区间表示为

2,4.考点二函数的判断【例2-1】（2020·浙江高一开学考试）下列各曲线中，不能表示y是x的函数的是（）A．B．C．D．【答案】C【解析】函数的定义：设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与

其对应，那么就说y是x的函数，x是自变量．如图，C选项中，在x允许的取值范围内取x＝x0，此时函数y与之对应的有2个值，y＝y1，y＝y2，不符合函数的定义.其它三个选项都符合函数的定义.故选：C．【例2-2】（2019·浙江湖州

.高一期中）下列对应关系是从集合A到集合B的函数的是（）A．AR，0Bxx，f：xyxB．AR，0Bxx，f：lnxyxC．AZ，BN，f：xyxD．AZ，BN，f：2xyx【答案】D【解析】A.AR，0Bxx，f：xyx

不是函数关系，∵当x＝0时，|0|＝0，|x|＞0不成立，∴不是函数关系；B.AR，0Bxx，f：lnxyx的定义域是0,，不是R，当0x时，lnyx无意义，∴不是函数关系；C.AZ，BN，f：xyx的定义域

是0,，不是Z，当x是负整数时，yx无意义，∴不是函数关系；D.AZ，BN，f：2xyx是函数关系.故选：D【一隅三反】1．（2020·上海高一课时练习）如图所示，表示函数图像的是（）A．B．C．D．【答案】B【解析

】根据函数的定义知，一个x有唯一的y对应，由图象可看出，只有选项B的图象满足这一点．故选：B．2．（2020·上海高一课时练习）下列各图中能作为函数图像的是（）．A．①②B．①③C．②④D．③④【答案】A【解析】对①②，对于定义域内的任意一个x，都有唯一的y值与

x对应，则①②正确；对③，在0,1x内，此时一个x有两个y值与x对应，则③错误；对④，在1,0x内，此时一个x有两个y值与x对应，则④错误；故选：A3．（2020·全国高一课时练习）判断下列对应是否为函数

：（1）x→y＝x，x∈{x|0≤x≤6}，y∈{y|0≤y≤3}；（2）x→y＝16x，x∈{x|0≤x≤6}，y∈{y|0≤y≤3}；（3）x→y＝3x＋1，x∈R，y∈R.【答案】（1）不是；（2）是；（3）是【解析】（1）根据函数概念知，当4x时，在|03yy没有值

与x对应，所以不是函数；（2）根据函数概念，当06|xxx时，1|016xxx，所以对于每一个x值，都有唯一的y值与之对应，所以是函数；（3）根据函数概念，对于每一个x值，都有唯一的y值与之对应，所以是

函数；考点三定义域【例3-1】（2020·上海高一开学考试）函数1212fxxx的定义域为（）A．0,2B．2,C．1,22,2D．,22,【答案】C【解析】由21020xx，解得x≥12

且x≠2．∴函数1212fxxx的定义域为1,22,2．故选：C．【例3-2】（2020·全国高一）已知(1)fx的定义域为(2,4)，（1）求()fx的定义域；（2）求(2)fx的定义域

【答案】（1）（3，5）；（2）35,22.【解析】（1）)1(fx的定义域为(2,4)，24x，则315x，即()fx的定义域为(3,5)；（2）()fx的定义域为(3,5)；由325x得3522

x，即(2)fx的定义域为35,22．抽象函数的定义域的求解，解抽象函数的定义域要抓住以下两点：（1）函数的定义域指的是自变量的取值范围；（2）对于函数fgx和fhx的定义域的求解，gx和hx的值域

相等，由此列不等式求出x的取值范围作为函数的定义域.（3）对于抽象函数定义域的求解，（1）若已知函数fx的定义域为,ab，则复合函数fgx的定义域由不等式agxb.（4）若复合函数fg

x的定义域为,ab，则函数fx的定义域为gx在,xab上的值域.【一隅三反】1．（2019·浙江高一期中）函数1()1fxxx的定义域是()A．RB．[1,)C．(,0)(0,)

D．[1,0)(0,)【答案】D【解析】由题意可得：10x，且0x，得到1x，且0x，故选：D2．（2019·内蒙古集宁一中高三月考）函数2132yxx的定义域为（）A．3,1B．1,3C．3,1D．0,1【答

案】A【解析】由2032xx，可得31x，所以函数2132yxx的定义域为(3,1).故选A.3．（2020·浙江高一课时练习）已知函数f(x)的定义域为(－1，0)，则函数f(2x＋1)的定义域为________．【答案】1(1

,)2【解析】由－1<2x＋1<0，得－1<x<－12，所以函数f(2x＋1)的定义域为1(1,)24．（2020·呼和浩特开来中学高二期末（文））设fx的定义域为0,2，则函数2fx的定义域是___________.【

答案】22，【解析】∵函数yfx的定义域为0,2，∴函数2yfx满足20,2x，解不等式202x，得22x，即函数2yfx的定义域是22，，故选A5．（2020·全国高一）已知函数fx的定义域为[1,2]，求gxfxf

x的定义域.【答案】[1,1]【解析】由题意，函数fx的定义域为[1,2]，则函数gxfxfx满足1212xx，解得1221xx，即11x

，即函数gx的定义域为[1,1].6（2020·全国高一）已知函数fx的定义域为[1，4]，求12fx的定义域.【答案】(,1]∪1,2.【解析】由1124x

，得112x，即110x或102x，解得x≤1，或12x.∴函数的定义域为(-∞，1]∪[12，+∞).考点四解析式【例4】（2020·全国高一课时练习）根据下列条件，求f(x)的解析式.（1）f(x)是一次函数，且满足3f

(x＋1)－f(x)＝2x＋9；（2）f(x＋1)＝x2＋4x＋1；（3）12()(0)ffxxxx.【答案】（1）f(x)＝x＋3；（2）f(x)＝x2＋2x－2；（3）2()(0)33xfxxx【解析】（1）解由

题意，设f(x)＝ax＋b(a≠0)∵3f(x＋1)－f(x)＝2x＋9∴3a(x＋1)＋3b－ax－b＝2x＋9，即2ax＋3a＋2b＝2x＋9，由恒等式性质，得22329aab∴a＝1，b＝3∴所求函

数解析式为f(x)＝x＋3.（2）设x＋1＝t，则x＝t－1f(t)＝(t－1)2＋4(t－1)＋1即f(t)＝t2＋2t－2.∴所求函数解析式为f(x)＝x2＋2x－2.（3）解1()2fxfxx，将原式中的x与1x互换，得112()ff

xxx.于是得关于f(x)的方程组12112fxfxxffxxx解得2()(0)33xfxxx.【一隅三反】1．（2020·全国高一课时练习）根据下列条

件，求f(x)的解析式.（1）f(f(x))＝2x－1，其中f(x)为一次函数；（2）f(2x＋1)＝6x＋5；（3）f(x)＋2f(－x)＝x2＋2x.【答案】（1）()212fxx或()212fxx

；（2）f(x)＝3x＋2；（3）21()23fxxx.【解析】（1）由题意，设f(x)＝ax＋b(a≠0)，则f(f(x))＝af(x)＋b＝a(ax＋b)＋b＝a2x＋ab＋b＝2x－1由恒等式性质，得22

1aabb212ab或212ab∴所求函数解析式为()212fxx或()212fxx（2）设2x＋1＝t，则12tx1()65322tftt∴f(x)＝3x＋2.（3）将x换成

－x，得f(－x)＋2f(x)＝x2－2x，∴联立以上两式消去f(－x)，得3f(x)＝x2－6x，21()23fxxx2．（2020·全国高一）（1）已知函数fx是一次函数，若48ffxx，求fx的解析式；（2）

已知fx是二次函数，且满足01f，12fxfxx，求fx的解析式．【答案】（1）823fxx或28fxx；（2）21fxxx．【解析】（1）设0fxaxba，

则2ffxfaxbaaxbbaxabb，又48ffxx，所以，248aabb，解得283ab或28ab，因此，823fxx或28fxx；（2）20fxaxbxc

a，则01fc，12fxfxx，即2211112axbxaxbxx，即22axabx，所以220aab，解得11ab.因此，21fxxx.3．（2019·山西高一月考

）（1）已知22112xfxx，求fx的解析式；（2）已知132gxgxx，求gx的解析式．【答案】（1）222511xxfxxx；（2）3188xgxx

【解析】（1）由题意得：12fx定义域为0xx设121txt，则12tx2222112521112tttftttt222511xxfxxx（2）

由132gxgxx…①得：1132ggxxx…②①②联立消去1gx得：3188xgxx考点五函数值【例5】（2020·浙江高一课时练习）若函数

221120xfxxx，那么12f（）A．1B．3C．15D．30【答案】C【解析】由于221120xfxxx，当14x时，11116151216f，故选C.【一隅三反】1．（2020·浙江杭州高二期末）已知2231fxxx

，则1f（）A．15B．21C．3D．0【答案】D【解析】根据fx的解析式，有21213112310f.故选：D2．（2020·上海高一课时练习）已知22()1xfxx，则111(1)(2)(3)(4)234fffffff

_________．【答案】72【解析】22()1xfxx，222211()()1111xxfxfxxx，22111211f所以111(1)(2)(3)(4)234fffffff111(

1)(2)(3)(4)234fffffff1711122故答案为：723．（2020·全国高一课时练习）若函数f(x)＝221xx，g(x)＝x，则2

fg的值为____________.【答案】23【解析】222222,22312gfgf.故答案为：234．（2018·浙江下城.杭州高级中学高一期中）若函数2212fxxx，则3f_______

_______．【答案】-1【解析】当213x时1x,故3f2211121f.故答案为：1考点六相等函数【例6】（2019·内蒙古集宁一中高三月考）下列四组函数中,表示同一函数的是（）A．2()

,()fxxgxxB．2(),()()fxxgxxC．21(),()11xfxgxxxD．2()11,()1fxxxgxx【答案】A【解析】对于A:()||fxx，2()||gxxx，两个函数的定义域和对应

关系都相同,表示同一函数；对于B:()fx的定义域为R,()gx的定义域为[0,),两个函数的定义域不同,不是同一函数;对于C.()1(1)fxxx的定义域为{|1}xx,()1gxx的定义域为

R,两个函数的定义域不同,不是同一函数;对于D.()fx的定义域为{|1}xx,()gx的定义域为{|1xx或1}x≥,两个函数的定义域不同,不是同一函数.故选A.【一隅三反】1．（2020·全国高一课时

练习）下列各组函数中，表示同一个函数的是__________(填序号).（1）y＝x－1和y＝211xx；（2）y＝x0和y＝1；（3）f(x)＝x2和g(x)＝(x＋1)2；（4）f(x)＝2xx和g(x)＝2xx.【答案】（4）【解

析】（1）1yx的定义域为R；211xyx的定义域为{|1}xx，定义域不同，故不是同一个函数；根据定义域和对应关系是否同时相等来判断是否为同一函数（2）0yx的定义域为{|0}xx；1

y的定义域为R，定义域不同，故不是同一个函数；（3）两个函数的对应关系不同，故不是同一个函数；（4）因为两个函数的定义域均为0,，且1fxgx，故两函数是同一个函数.故答案为：（4）2．（2020·全国高一课时练习）下列函数2()yx；2xyx；3

3yx；2yx与函数yx是同一函数的是________.【答案】33yx【解析】2()yx定义域是[0,)，所以与函数yx不是同一函数；2xyx定义域是(,0][0,)，所以与函数yx不是同一函数；33

yxx，所以与函数yx是同一函数；2=yxx，所以与函数yx不是同一函数.故答案为：33yx3．（2020·全国高一课时练习）下列对应或关系式中是A到B的函数的序号为________.①，ARBR，221xy；②A＝{1，2，3，4}

，B＝{0，1}，对应关系如图：③，ARBR，1:2fxyx；④，AZBZ，:21fxyx.【答案】②【解析】①，ARBR，221xy，存在x对应两个y的情况，所以不是A到B的函数；②符合函数的定义，是A到B的函数；③，A

RBR，1:2fxyx，对于集合A中的2x没有对应y，所以不是A到B的函数；④，AZBZ，:21fxyx，对于集合A中的{|0,}xxxz没有对应y，所以不是A到B的函数.故答案为：②考点七分段函数【例7-1】（2020·上海高一开学考试）已知函

数2,01,()2,12,1,2,2xxfxxx，则3[()]2fff的值为（）A．1B．2C．3D．12【答案】A【解析】由题意得,3()=22f,1(2)=2f,1()=2=1122f,所以3[()]=[(2)]=()

=1212ffffff,故选：A.【例7-2】（2020·全国高一课时练习）设函数若f（a）＝4，则实数a＝（）A．－4或－2B．－4或2C．－2或4D．－2或2【答案】B【解析】当0a时，()4faa，

解得4a；当0a时，24()faa，解得2a，因为0a，所以2a，综上，4a或2，故答案选B【一隅三反】1．（2020·全国高一课时练习）设1,01,01,0xxfxxx，则0ff等于（）A．1B．0C．2D．

-1【答案】C【解析】1,0()1,01,0xxfxxx(0)1f,((0))(1)112fff.故选:C.2．（2020·全国高一课时练习）已知函数y＝21,02,0xxxx，则使函数值为5的x的值是（）A．2或2B．2或52C

．2D．2或2或52【答案】C【解析】当0x时，令5y，得215x，解得2x；当0x时，令5y，得25x，解得52x，不合乎题意，舍去.综上所述，2x.故选：C.3．（2020·全国高一课时练习）已知2,11

()1,11,1xxfxxx（1）画出f(x)的图象；（2）若1()4fx，求x的值；（3）若1()4fx，求x的取值范围.【答案】（1）作图见解析；（2）12x；（3）11,,22

【解析】（1）函数2yx=的对称轴0x，当0x时，0y；当1x时，1y；当1x时，1y，则f(x)的图象如图所示.（2）1()4fx等价于21114xx①或1114x②或

1114x③解①得12x，②③的解集都为∴当1()4fx时，12x.（3）由于1124f，结合此函数图象可知,使1()4fx的x的取值范围是11,,22

