【文档说明】2021年高中数学人教版必修第一册：2.2《基本不等式》精品讲义(含解析).doc，共(12)页，697.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31206.html

以下为本文档部分文字说明：

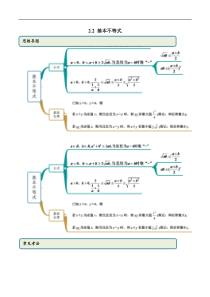
2.2基本不等式思维导图常见考法考点一公式的直接运用【例1】（1）（2020·全国高一课时练习）若102a，则12aa的最大值是（）A．18B．14C．12D．1（2）（2020·全国高一课时练习）已知1x，求函数11yx

x的最小值是（)A．4B．3C．2D．1【答案】（1）A（2）D【解析】（1）102a，故120a，则2212111122122228aaaaaa，当14a时取“=”，所以正确选项为A（2）由1x，即10x，所以111

112111111yxxxxxx，0x时取“=”，所以正确选项为D【一隅三反】考查基本不等式，采用构造法，基本不等式需注意：“一正二定三相等”缺一不可。一不可1．（2020·全国高一课时练习）若1a，则11aa的最小值是()A．1B．2C．3

D．4【答案】C【解析】1a则10a，1111311aaaa，当2a时取“=”，所以正确选项为C2．（2020·上海高一开学考试）已知2x，函数42yxx的最小值是（）A．5B．4C．8D．6【答案】D【解析】因为该函数的单调性较难求，所以可以考虑用不等

式来求最小值，，因为，由重要不等式可知，所以，本题正确选项为D.3．（2020·全国高一课时练习）已知函数()4(0,0)afxxxax在3x时取得最小值，则a________．【答案】36【解析】因为()4(0,0)afxxxax，所以，当且仅

当即，由题意，解得考点二条件型【例2】（1）（2020·全国高一课时练习）已知实数0,0,31xyxy，则11xy的最小值为（)A．6B．223C．43D．423（2）（2020·哈尔滨德强学校高一期末）已知实数0a，0b，11111a

b，则2ab的最小值是（）A．32B．22C．3D．2【答案】（1）D（2）B【解析】（1）1111334423yxxyxyxyxy，正确选项为D（2）∵0a，0b，11111ab

112(1)12(1)2(1)3[(1)2(1)]()3[12]31111baababababab3+223=22当且仅当2(1)111baab，即2

a，22b时取等号.故选B【一隅三反】1．（2020·全国高一开学考试）已知0,0,1xyxy,则11xy的最小值是()A．2B．22C．4D．23【答案】C【解析】11112224yxy

xxyxyxyxyxy（当且仅当yxxy，即xy时取等号）11xy的最小值为4故选：C2．（2020·四川金牛。成都外国语学校高一期末（文））若正数x，y满足1

35yx，则34xy的最小值是（）A．245B．285C．5D．25【答案】C【解析】正数x，y满足135yx，则11313121434(34)()1313325555xyxyxyxyyxyxyx，当且仅当21xy时取等号．34

xy的最小值是5．故选：C．3．（2020·全国高一课时练习）已知0,0ab，122ab，则ab的最小值为_______________；条件型（乘K法）：和为定值K，求倒数和的最小值，采用乘K法【答案】3222【解析】

采用常数1的替换，11212123223322222babaababababab，当2baab即1222,22ab时等号成立，所以答案为3222．考点三配凑型【例3】（1）（2020·衡水市

第十三中学高一月考）已知23601xxfxxx，则fx的最小值是________．（2）（2019·四川高一期末）已知正数x、y满足1xy，则141xy的最小值为【答案】（1）5（2）92【

解析】当0x时，11x，232444211111xxfxxxxxx421151xx，当且仅当411xx，即当1x时，等号成立，因此，函数0yfxx的最小值为5.故答案为：5.（2）1xy，所以，(1)2

xy，则141441412()[(1)]()52591111xyxyxyxyxyyxyx…，所以，14912xy…，当且仅当4111xyyxxy，即当2313xy

时，等号成立，因此，141xy的最小值为92，故选：B．【一隅三反】1（2020·全国高一专题练习）设1x，求521xxyx的最大值.【答案】1【解析】∵1x，∴10x∴10x所以22521514710415

1111xxxxxxyxxxxx4152451(1)xx当且仅当2(1)4x，即3x时等号成立所以521xxyx的最大值为12．（2

020·全国高一课时练习）函数233(1)1xxyxx的最小值为（）A．3B．2C．1D．1【答案】A【解析】1x，则10x，22111331113111xxxxyxxxx

，当0x时取“=”，所以正确选项为A．3．（2020·全国高一课时练习）已知52x…，则24524xxfxx有()A．最大值54B．最小值54C．最大值1D．最小值1【答案】D1.分子分母为一次函数和二次函数，把二次函数配凑成关系一次

函数的一元二次，再分子分母同除一次函数2.给出等式但是不符合条件型，则从分母入手，分母相加减可得到等式的关系的倍数，即降次-配凑-均值不等式【解析】2245(2)11111()(2)2(2)1242(2)2222xxxfxxxxxxx

…当且仅当122xx即3x时取等号，故选：D．考点四换元法【例4】（2019·河北路南.唐山一中高三期中（文））已知x>0，y>0,x+2y+2xy=8，则x+2y的最小值是()A．3B．4C．92D．112【答案】B【解析

】考察均值不等式2228(2)82xyxyxy，整理得2(2)4(2)320xyxy即(24)(28)0xyxy，又x+2y>0，24xy【一隅三反】1．（2020·上海高一开学考试）若正数,x

y满足220xxy，则3xy的最小值是（）A．4B．22C．2D．42【答案】A【解析】因为正数,xy满足220xxy，所以2yxx，所以2232224xyxxxx，当且仅当22xx，即1x时，等号成立.故选：A2．（2020·江西高一期末

）已知a，0b，且满足21aab，则3ab的最小值为（）A．2B．3C．22D．23【答案】C【解析】∵21aab，∴1baa．即1113322222abaaaaaaa．当且仅当22a时取等号．∴3ab的最小值

为22故选：C3．（2020·黑龙江工农.鹤岗一中高一期末（理））若正数,xy满足40xyxy，则3xy的最大值为（）A．13B．38C．37D．1【答案】A【解析】因为40xyxy，化简可得4xyxy，左右两边同时除以xy得141yx求

3xy的最大值，即求333xyxy的最小值所以1413333xyxyyx4143333xyyx41423333xyyx3，当且仅当433x

yyx时取等号所以3xy的最大值为13所以选A4．（2020·浙江高三月考）已知实数,xy满足22455xxyy，则222xy的最小值为（）A．53B．103C．109D．4【答案】B【解析】设222xym，则222

xmy，22455xxyy，22455xyxy，则222221655xyxy，222216257ymymy，42281(3070)(5)0ymym，

设2yt，则2281(3070)(5)0tmtm，22(3070)481(5)0mm…，解得103m，222xy的最小值为103.故选：B考点五求参数【例5】（2020·浙

江高一单元测试）已知不等式19axyxy≥对任意实数x、y恒成立，则实数a的最小值为（）A．8B．6C．4D．2【答案】C【解析】11aaxyxyaxyyx.若0xy，则0yx，从而1axyayx无最小值，不合乎题

意；若0xy，则0yx，0xy.①当0a时，1axyayx无最小值，不合乎题意；②当0a时，111axyyayxx，则19axyxy≥不恒成立；③当0a时，21121211aaxyaxyxyaaaaaxyyxyx

，当且仅当yax时，等号成立.所以，219a，解得4a，因此，实数a的最小值为4.故选：C.【一隅三反】1．（2020·河北路南.唐山一中高一期中）若对于任意20,31xxaxx

恒成立，则a的取值范围是（）A．1,5B．1[,)5C．(0,)D．(5,)【答案】B【解析】因为0x，所以211313xxxxx，因为0x，所以12xx（当且仅当1x时取

等号），则11113253xx，即231xxx的最大值为15，故15a.故选：B2．（2020·河南高三其他（理））若对任意正数x，不等式22214axx恒成立，则实数a的取值范围为（）A．0,B．1,4

C．1,4D．1,2【答案】B【解析】依题意得当0x时，2222144xaxxx恒成立，又因为4424xxxx，当且仅当2x时取等号，所以24xx的最大值为12，所以1212a，解得14a，因此，实数a的取值范围为

1,4.故选：B.3．（2020·西夏.宁夏大学附属中学高二月考（文））若两个正实数x，y满足211xy，且222xymm恒成立，则实数m的取值范围是（）A．,24,B．,42,C

．4,2D．2,4【答案】C【解析】由题意，两个正实数x，y满足211xy，则21442(2)()4428yxyxxyxyxyxyxy，当且仅当4yxxy，即4

,2xy时，等号成立，又由222xymm恒成立，可得228mm，即(4)(2)0mx，解得42m，即实数m的取值范围是4,2.故选：C.考点六实际应用题【例6】（2020·浙江高一课时练习）某工厂拟建一个平面图形为矩形，且总面积为40

0平方米的三级污水处理池，如图R3－1所示.已知池外墙造价为每米200元，中间两条隔墙造价为每米250元，池底造价为每平方米80元（池壁的厚度忽略不计，且污水处理池无盖）.若使污水处理池的总造价最低，那么污水处理池的长和宽分别为（）A．40米，10米B．20米，20米C．30米,4

03米D．50米，8米【答案】C【解析】设污水池的宽为x米，则长为400x米，总造价为y，则4001600002002222508040090032000yxxxxx16000029003200056000xx（元），当且仅当1600009

00xx时，即当403x时，总造价最低，此时，污水池的宽为403米，长为30米.故选：C.【一隅三反】1．（2019·全国高一课时练习）设计用的材料制造某种长方体形状的无盖车厢，按交通部门的规定车厢宽度为，则车厢的最大容积是（）A．（38－3m3B．16m3C．4

m3D．14m3【答案】B【解析】设长方体车厢的长为xm，高为hm，则，即，∴，即，解得，∴．∴车厢的容积为．当且仅当且，即时等号成立．∴车厢容积的最大值为．选B．2．（2020·全国高一课时练习）将一根铁丝切割成三段，做一个面积为22m，形状为直角三角形的框架，在下列4种长度的铁丝中，选用最合

理共用且浪费最少的是()A．6.5mB．6.8mC．7mD．7.2m【答案】C【解析】设直角三角形的框架的两条直角边为x，y（x＞0，y＞0）则xy＝4，此时三角形框架的周长C为：x+y+22xy＝x+y+2(

)8xy∵x+y≥2xy＝4∴C＝x+y+22xy≥4+22≈6.83故用7米的铁丝最合适．故选C．3．（2020·全国高一课时练习）某公司一年需要购买某种原材料400吨，计划每次购买x吨，已知每次的运费为4万元/次，一年总的库存费用为4x万元，为了

使总的费用最低，每次购买的数量x为_____________；【答案】20吨【解析】由题意，总的费用400400444160yxxxx，当20x=时取“=”，所以答案为20吨。