【文档说明】北京市房山区2021-2022学年高一上学期数学期末试卷及答案.docx，共(7)页，508.181 KB，由baby熊上传

转载请保留链接：https://www.ichengzhen.cn/view-108007.html

以下为本文档部分文字说明：

1/72022北京房山高一（上）期末数学一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项符合题目要求。（1）化简23x的结果是（A）23x（B）32x（C）16x（

D）6x（2）下列函数中，值域是R的幂函数是（A）13yx=（B）13xy骣琪=琪桫（C）23yx=（D）23xy骣琪=琪桫（3）某校高一共有10个班，编号分别为01，02，...，10，现用抽签法从中抽取3个班进行调查，设高一(5)班被抽到的概率为a，高一(6)班被抽到的概率为b，则（

A）310a=，29b=（B）110a=，19b=（C）310a=，310b=（D）110a=，110b=（4）下列函数中，既是奇函数又在区间(0,)+上单调递增的是（A）12+−=xy（B）xy2log=（C）3xy=（D）xy=（5）已知函数()2xfx=的反函数是(

)ygx=，则1()2g的值为（A）1（B）21（C）12−（D）1−（6）为了丰富学生的假期生活，某学校为学生推荐了《西游记》、《红楼梦》、《水浒传》和《三国演义》4部名著．甲同学准备从中任意选择2部进行阅读，那么《红楼梦》被选中

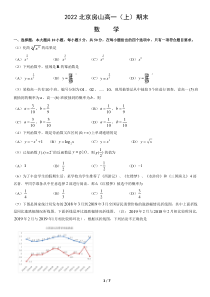
的概率为（A）14（B）13（C）12（D）34（7）下图是国家统计局发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图，其中上面折线是同比涨跌幅情况折线图，下面折线是环比涨跌幅情况折线图，（注：2019年2月与2018年

2月相比较称同比，2019年2月与2019年1月相比较称环比），根据该折线图，下列结论不正确的是2/7（A）2018年3月至2019年3月全国居民消费价格同比均上涨（B）2018年3月至2019年3月全国居民消费价格环比有涨有跌（C）2019年3月全国居民消费价格同比涨幅最大（D）

2019年3月全国居民消费价格环比变化最快（8）设函数21,2()2log(1),2xxfxxxì骣ï琪<ï琪=í桫ï-ïî≥，若1)(xf，则x的取值范围是（A）)3,0(（B）),3()0,(+−（C）),2

()1,(+−−（D）)2,1(−(9)某食品的保鲜时间y（单位：小时）与储藏温度x（单位：C）满足函数关系ekxby+=（e2.718=为自然对数的底数，,kb为常数）．若该食品在0C的保鲜时间是

192小时，在33C的保鲜时间是24小时，则该食品在22C的保鲜时间是（A）20小时（B）24小时（C）36小时（D）48小时（10）已知函数()yfx=，若在定义域内存在实数x，使得()()fxkfx−=−，其中k为整数，则称函数()yfx=为

定义域上的“k阶局部奇函数”，若()()2logfxxm=+是1,1−上的“1阶局部奇函数”，则实数m的取值范围是（A）1,2（B）(1,2（C）2,2−（D）1,2−

二、填空题：本大题共5小题，每小题5分，共25分。（11）已知事件A与事件B是互斥事件，若事件A与事件B同时发生的概率记为p，则p=_______.（12）函数=lg+2yxx-的定义域是______

_.（13）甲、乙两名射击运动员在某次测试中各射击20次，两人的测试成绩如下表：甲的成绩环数78910频数5555乙的成绩环数78910频数6446若1x，2x分别表示甲、乙两名运动员的这次测试成绩的平均数，则1x，2x的大小关系是_______；若1s，2s分别表示甲、乙两名运动员的这次

测试成绩的标准差，则1s，2s的大小关系是_______.（14）已知13(3)a=-，232.5b=，23(1.4)c-=，则cba,,的大小关系为_______.（15）试写出函数()fx，使得()fx同时满足以下条件：①定义域为)0,+；②值域为)0,+；③在定义域内是单调增函数

.则函数()fx的解析式可以是_______（写出一个满足题目条件的解析式）.3/7三、解答题：本大题共5小题，每题15分，共75分。（16）（本小题满分15分）已知幂函数()fxx=的图象经过点(2,2)．(Ⅰ)求函数()fx的解析式；(Ⅱ)若函数(

)fx满足条件(2)(1)fafa−−，试求实数a的取值范围．（17）（本小题满分15分）在创建文明城市活动中，房山区某单位共有100名文明交通义务劝导志愿者（简称为志愿者），他们每周三和每周五的上午8:009:00，下午5:006:00上下班的高峰时段，在

红绿灯路口义务执勤，劝导行人自觉遵守交通规则，该单位对他们自2021年9月至12月参加活动的次数统计如下图所示.区创城办为了解市民文明出行情况，采用分层抽样的方法从该单位参加1次和3次的志愿者中抽取5人进行访谈.(Ⅰ)求该单位志愿者参加活动的人均次数；(Ⅱ)这5人中参

加1次和3次活动的志愿者各占多少人？(Ⅲ)从这5人中随机抽取2人完成访谈问卷，求2人中恰有1名参加1次活动的志愿者的概率.（18）（本小题满分15分）已知函数()113xfx+=.(Ⅰ)判断函数()fx的单调性，并进行证明；(Ⅱ)设()()()12gxfxx

=−≥，求函数()gx的值域.（19）（本小题满分15分）已知函数0()1(log)(+=abxxfa且)1a，1)1(=f，2)3(=f.(Ⅰ)求函数)(xf的解析式；(Ⅱ)若()gx()()fxfx=--，指出函数)(xg的奇偶性，并证明

．4/7（20）（本小题满分15分）为落实国家“精准扶贫”政策，某企业于2020年在其扶贫基地投入200万元研发资金，用于养殖业发展，并计划今后7年内在此基础上，每年投入的资金比上一年增长15%．(Ⅰ)写出第x年（20

21年为第一年）该企业投入的资金数y（万元）与x的函数关系式，并指出函数的定义域；(Ⅱ)该企业从第几年开始（2021年为第一年），每年投入的资金数将超过400万元？（参考数据：lg0.150.824−,lg1.50.176，lg0.1150.93

9−，lg1.150.061，lg20.301）5/72022北京房山高一（上）期末数学参考答案一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项符合题目要求。题号12345678910答案（A）（A）

（C）（C）（D）（C）（C）（B）（D）（B）二、填空题：本大题共5小题，每小题5分，共25分。（11）0（12）(]0,2（13）12xx=，12ss<或21ss>（14）bca>>或acb<<（15

）答案不唯一，113244(),(),()fxxfxxfxx===；()2()0fxxx=≥，()()0fxxx=≥．三、解答题：本大题共5小题，每题15分，共75分。（16）解：(Ⅰ)因为()22a=，所以2a=．所以()2fxx=．....

.......5分(Ⅱ)因为()()21fafa>--，所以()()2221aa>--．所以224421aaaa-+>-+．所以23a<．所以32a<．所以满足条件()()21fafa->-的实数a的取值范围为3,2骣琪-?琪桫．...........1

5分（17）解：(Ⅰ)参加1次的志愿者有20人，2次的志愿者有50人，3次的志愿者有30人1202503302.1100???=．所以该校志愿者参加活动的人均次数为2.1．...........3分(Ⅱ)这5人中参加1次活动的志愿者有20522030?+；这5人中参加3次活动的志愿者有305

32030?+．所以这5人中参加1次和3次活动的志愿者分别占2人、3人．...........7分(Ⅲ)设参加1次活动的2名志愿者分别为12,aa，参加3次活动的3名志愿者分别为123,,bbb，则基本事件空间为()()()()()()()()()(){}12111213212223

121323,,,,,,,,,,,,,,,,,,,aaababababababbbbbbb6/7所以10n=．设“从这5人中随机抽取2人完成访谈问卷，这2人中恰有1名参加1次活动的志愿者”为事件A，则()()()

()()(){}111213212223,,,,,,,,,,,Aabababababab=，所以6m=．所以()63105mPAn===．...........15分（18）解：(Ⅰ)函数()113xfx+=是(),−+上的减函数...........

.2分任意()12,,xx−+，且12xx，则1211xx++.因为1013，所以12111133xx++.所以()()12fxfx.所以函数()113xfx+=是(

),−+上的减函数．...........9分(Ⅱ)因为()113xfx+=是(),−+上的减函数，所以()()11123xgxx+=−≥是减函数.所以当2x=时，()gx有最大值2627−.又因为当2x≥时

，1103x+，所以11113x+−−．所以()()()12gxfxx=−≥的值域为261,27−−............15分（19）解：(Ⅰ)因为==2)3(1)1(ff，即=+=+2)31(log1)1(log

bbaa，化简为2113babaì+=ïí+=ïî，解得21ab==或10ab==(舍）．所以函数()()2log1fxx=+．...........6分(Ⅱ)()()()gxfxfx=--是奇函数．因为2()log(1)fxx=+，所以()()()gfxfxx=−−7/

7()()221logog1lxx−=+−因为1010xx+−，即11xx−，所以11x−．所以()gx的定义域为()1,1−，关于原点对称．()()22log1(log1)gxxx−−=+−()()()22log1log1()xxgx=−+−−=−所以函数

()gx是定义在()1,1−上的奇函数．...........15分（20）解：(Ⅰ)第一年投入的资金数为200(115%)+万元，第二年投入的资金数为2200(115%)200(115%)15%200(115%)+++=+万元，第x年（2021年为第一年）该企业投入的资金数y（万元）与

x的函数关系式为200(115%)xy=+，其定义域为*7xxN∣1剟．...........7分(Ⅱ)由200(115%)400x+，可得1.152x，即lg2lg1.15x，因为lg20.3014.93lg1.150.061，所以5x≥．即该企业从第5年,就是从2

025年开始，每年投入的资金数将超过400万元．...........15分