【文档说明】2021年人教版高中数学必修第二册(精讲)8.6《空间直线、平面的垂直》（1）（原卷版）.doc，共(10)页，536.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38708.html

以下为本文档部分文字说明：

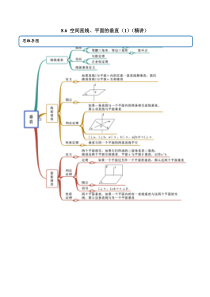
8.6空间直线、平面的垂直（1）（精讲）思维导图考法一线面垂直【例1】（2021·江西景德镇市·景德镇一中）在四棱锥PABCD中，90ABCACD，常见考法60BACCAD，PA平面ABC

D，E为PD的中点，M为AD的中点，24PAAB．（1）取PC中点F，证明：PC平面AEF；（2）求点D到平面ACE的距离.【一隅三反】1．（2021·陕西省黄陵县中学高一期末）如图所示，AB为O的直径，C为O上一点，AD平面ABC，AEBD于E，AFCD于F.求证：

BD平面AEF.2．（2021·宁夏银川市·银川一中高一期末）如图，在三棱锥PABC中，PA平面ABC，底面ABC是直角三角形，4PAABBC，O是棱AC的中点，G是AOB的重心，D是PA的中点.（1）求证：BC⊥平面PAB；（2

）求证：DG//平面PBC；3．（2021·陕西咸阳市·高一期末）将棱长为2的正方体1111ABCDABCD沿平面11ABCD截去一半（如图1所示）得到如图2所示的几何体，点E，F分别是BC，DC的中点.（Ⅰ）证明：EF平面1AAC；（Ⅱ）求三棱锥1ADEF的体积.考法二线线

垂直【例2】（2020·全国专题练习）如图，在三棱柱111ABCABC中，侧面11ABBA为矩形，11,2ABAA==，D是1AA的中点，BD与1AB交于点O，且CO平面11ABBA(1)证明：1BCAB；(2)若2OCOA，求三棱柱111ABCABC的高.【一隅

三反】1．（2021·西安市航天城第一中学高一期末）如图，在三棱柱ABCABC中，侧棱CC⊥底面ABC，ABAC，,,DEF分别为棱,,AABBBC的中点．（1）求证：BCAF；（2）若2

,22,ABBCCC求三棱锥DAEF的体积．2．（2021·广西河池市·高一期末）如图，在三棱柱111ABCABC中，11ACCBCC，ACBC．（1）若三棱柱111ABCABC的体积为1，求三棱锥1CABC的体积；（2）证明：1ABCC．3．（

2021·扶风县法门高中高一期末）如图，三棱锥V—ABC中，VA=VB＝AC=BC=2，AB＝23，VC=1．（1）证明：AB⊥VC；（2）求三棱锥V—ABC的体积．考法三面面垂直【例3】（2021·江西景德镇市·景德镇一中高一期末）如图，四棱锥P

ABCD中，底面ABCD是正方形，PD平面ABCD，226ABPD，，O为AC与BD的交点，E为棱PB上一点.（1）证明：平面EAC平面PBD；（2）若//PD平面EAC，求三棱锥BAEC的体积.【一隅三反】1．（2021·陕西宝鸡市·高一期末）如图，在三棱锥PABC中，PAAB，

PABC，ABBC，2PAABBC，D为线段AC的中点，E为线段PC上一点．（1）求证：平面BDE平面PAC；（2）当//PA面BDE时，求三棱锥EBCD的体积．2．（2021·全国高一课时练习）在四棱锥PABCD中，底面ABCD为矩形，AP

平面PCD，E，F分别为PC，AB的中点求证：（1）平面PAD平面ABCD；（2）//EF平面PAD3．（2021·全国高一课时练习）如图所示，已知在三棱锥ABPC中，,APPCACBC，M为AB的中点，D为PB的中点，且PMB△为正三角形．（Ⅰ）求证：//DM平面APC；（

Ⅱ）求证：平面ABC平面APC；（Ⅲ）若4,20BCAB，求三棱锥DBCM的体积．考法四空间距离【例4】（2020·全国专题练习）在棱长为a的正方体1111ABCDABCD中求出下列距离：（1）点A到面11BBC

C的距离；（2）线段11BD到面ABCD的距离；（3）点A到面11BBDD的距离；（4）C到平面1BDC的距离.【一隅三反】1．（2020·北京二十中高一期末）如图，正四棱锥PABCD的高为2，且底面边长也为2，则点A到平面PBC的

距离为（）A．455B．255C．54D．522．（2020·全国）已知正四棱柱ABCD-A1B1C1D1中，AB=2，CC1=22E为CC1的中点，则直线AC1与平面BED的距离为A．2B．3C．2D．13．（2020·全国高一课时练习）已知1111AB

CDABCD是长方体，且4AB，3AD，12AA.（1）写出点A到平面11BCCB的距离；（2）写出直线AB到平面1111DCBA的距离；（3）写出平面11ADDA与平面11BCCB之间的距离.