【文档说明】2021年人教版高中数学必修第二册(精讲)8.6《空间直线、平面的垂直》（1）（解析版）.doc，共(20)页，1.275 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38896.html

以下为本文档部分文字说明：

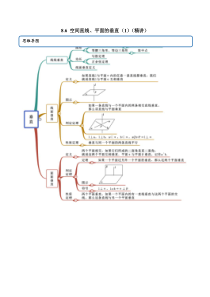
8.6空间直线、平面的垂直（1）（精讲）思维导图考法一线面垂直【例1】（2021·江西景德镇市·景德镇一中）在四棱锥PABCD中，90ABCACD，常见考法60BACCAD，PA平面ABCD，E为PD的中点，M为AD的中点，24PAAB

．（1）取PC中点F，证明：PC平面AEF；（2）求点D到平面ACE的距离.【答案】（1）证明见解析；（2）23【解析】（1）证明:因为PC中点F，在RtABC中，2,60ABBAC，则23,4BCAC．而4PA，则在等腰三角形APC中，PCAF①.又在P

CD中，,PEEDPFFC,则//EFCD，因为PA平面ABCD，CD平面ABCD，则PACD，又90ACD，即ACCD，ACPAA，则CD平面PAC，因为PC平面PAC，所以PCCD，因此EFPC

②.又EFAFF，由①②知PC平面AEF；（2）在RtACD△中，43,4CDAC，83ACDS，又//EMPA，PA平面ABCD，EM平面ABCD，即EM为三棱锥EACD的高，11163832333EACDACDVS

EM，在ACE△中，254AECEAC，，8ACES，设点D到平面ACE的距离为h，则116333DACEEACDACEVVSh，23h，即点D到平面ACE的距离为23.【一隅三反】1．（2021·陕西省黄陵县中学高一期末）

如图所示，AB为O的直径，C为O上一点，AD平面ABC，AEBD于E，AFCD于F.求证：BD平面AEF.【答案】证明见解析【解析】证明：AB为⊙O的直径，C为⊙O上点，所以BCAC因为DA平面ABC，BC平面ABC，所以DABC又DAACA,所

以BC⊥面DAC又AF平面DAC，则BCAF又AFDC，DCBCCI，所以AF平面BCD又BD平面BCD，所以AFBD又因为AEBD，AEAFA所以BD平面AEF2．（2021·宁夏银川市·银川一中高一期末）如图

，在三棱锥PABC中，PA平面ABC，底面ABC是直角三角形，4PAABBC，O是棱AC的中点，G是AOB的重心，D是PA的中点.（1）求证：BC⊥平面PAB；（2）求证：DG//平面PBC；【答案】（1）证明见解

析；（2）证明见解析.【解析】（1）证明：PA平面ABC，且BC平面ABC，PABC，底面ABC是直角三角形且ABBC，ABBC，又PA平面PAB，ABÌ平面PAB，PAABA，BC⊥平面PAB.(2)证明：连结OG并延长交AB于

点E，连结DO，DE,G是AOB的重心，OE为AB边上的中线，E为AB边上的中点，又有D为PA边上的中点，//DEPB，PB平面PBC，//DE平面PBC，同理可得//DO平面PBC，又DE平面DOE，DO平面

DOE，DEDOD，平面DOE//平面PBC，又有DG平面DOE，DG//平面PBC3．（2021·陕西咸阳市·高一期末）将棱长为2的正方体1111ABCDABCD沿平面11ABCD截去一半（如图1所示）得到如图2所示的几何体，点E，F分别是BC，DC的中点.

（Ⅰ）证明：EF平面1AAC；（Ⅱ）求三棱锥1ADEF的体积.【答案】（Ⅰ）证明见解析；（Ⅱ）1.【解析】（Ⅰ）如图所示：连接BD，易知BDAC，因为1AA平面ABCD，BD平面ABCD，所以1AABD，又1AAACAI，所以BD平面1AAC.在CBD中，点E，F分别是B

C，DC的中点，所以//BDEF.所以EF平面1AAC.（Ⅱ）∵1DD平面ABCD，∴1DD是三棱锥1DAEF在平面AEF上的高，且12DD.∵点E，F分别是BC，DC的中点，∴1DFCFCEBE.∴2

111322222AEFSADDFCFCEABBE△.∴11111321332ADEFDAEFAEFVVSDD△.考法二线线垂直【例2】（2020·全国专题练习）如图，在三棱柱111ABCABC中，侧面11ABBA为矩形，11,2ABAA==，

D是1AA的中点，BD与1AB交于点O，且CO平面11ABBA(1)证明：1BCAB；(2)若2OCOA，求三棱柱111ABCABC的高.【答案】（1）证明见解析；（2）62.【解析】（1）证明：由题意2216,3.2BDABADAB且1AODBOB,111.2AODOADO

BOBBB163,363ODBDAO222AOODAD,所以1ABBD,又CO侧面11ABBA，1ABCO,又BD与CO交于点O，所以,1AB平面CBD又因为BC平面CBD,所以1BCAB．(2)在矩

形11ABBA中，由平面几何知识可知36,33OAOB∵2OCOA，∴63OC，∴2321,,33ABCACBCS设三棱柱111-ABCABC的高为h，即三棱锥1AABC的高为h又122ABAS

，由11CABAAABCVV＝得1··ABCABAShSOC，∴62h【一隅三反】1．（2021·西安市航天城第一中学高一期末）如图，在三棱柱ABCABC中，侧棱CC⊥底面ABC

，ABAC，,,DEF分别为棱,,AABBBC的中点．（1）求证：BCAF；（2）若2,22,ABBCCC求三棱锥DAEF的体积．【答案】（1）见解析；（2）23.【解析】（1）因为侧棱CC

⊥底面ABC，AF平面ABC，所以CCAF，因为F为中点，ABAC，故BCAF，而CCBCC，故AF平面BCC，而BC平面BCC，故BCAF.（2）取AB的中点为G，连接FG.因为2,22ABACBC，故222BCAC

AB，故ACAB，因为,CFFBAGGB，故//FGAC，且1FG，故FGAB，因为三棱柱ABCABC中，侧棱CC⊥底面ABC，故三棱柱ABCABC为直棱柱，故BB⊥底面A

BC，因为FG底面ABC，故BBFG，而BBABB，故FG平面ADE，而1112244ADESADABAAABCCAB，故122133ADEFFADEVV.2．（2021·广西

河池市·高一期末）如图，在三棱柱111ABCABC中，11ACCBCC，ACBC．（1）若三棱柱111ABCABC的体积为1，求三棱锥1CABC的体积；（2）证明：1ABCC．【答案】（1）13；（2）证明见解析.【解析】（1）设三棱柱

111ABCABC的高为h，ABC的面积为S，由三棱柱111ABCABC的体积为1，可得1111ABCABCVSh，可得三棱锥1CABC的体积为1133Sh.（2）如图所示：取AB的中点D，连CD，1CD,∵1111ACB

CCCCCACCBCC，∴11ACCBCC≌，∴11ACBC,∵ADDB，11ACBC，∴1ABCD∵ADDB，ACBC，∴ABCD,∵1ABCD，ABCD，1,CDCD平面1CDC，1CDCDD，∴AB平面1CDC∵AB

平面1CDC，1CC平面1CCD，∴1ABCC．3．（2021·扶风县法门高中高一期末）如图，三棱锥V—ABC中，VA=VB＝AC=BC=2，AB＝23，VC=1．（1）证明：AB⊥VC；（2）

求三棱锥V—ABC的体积．【答案】（1）证明见解析；（2）12.【解析】（1）证明：取AB的中点为D，连接VD，CD，∵VA=VB，ABV是等腰三角形，∴AB⊥VD，ACBC，ABC是等腰三角形，AB⊥CD，VDCDD，所以AB⊥平

面VDC．又VC平面VDC，故AB⊥VC.（2）由（1）知AB⊥平面VDC，132ADAB，2VA=，所以221VDVAAD，2AC，221CDACAD，又VC=1，所以VDC是等边三

角形，所以1133sin60112224VDCSVDDC，故三棱锥V—ABC的体积等于1131233342VDCSAB．考法三面面垂直【例3】（2021·江西景德镇市·景德镇一中高一期末）如图，四棱锥PABCD中，底面ABCD是正

方形，PD平面ABCD，226ABPD，，O为AC与BD的交点，E为棱PB上一点.（1）证明：平面EAC平面PBD；（2）若//PD平面EAC，求三棱锥BAEC的体积.【答案】（1）证明见解析；（2）263.【解析】（1）因为四边形ABCD为正方形，则ACBD，PD底

面ABCD，AC平面ABCD，ACPD，PDBDD，AC平面PBD，AC平面EAC，平面EAC平面PBD；（2）如下图所示，连接OE，四边形ABCD为正方形，且ACBDO，则O为BD的中点，因为//PD平面AEC，PD平面PBD，平面PBD平面AECOE

，//OEPD，O为BD的中点，E为PB的中点，PD平面ABCD，OE平面ABCD，且162OEPD，ABC的面积为21222ABCS△，所以，112626333BAECEABCABCVVSOE△.【一隅三反】1．（2

021·陕西宝鸡市·高一期末）如图，在三棱锥PABC中，PAAB，PABC，ABBC，2PAABBC，D为线段AC的中点，E为线段PC上一点．（1）求证：平面BDE平面PAC；（2）当//PA面BDE时，求三棱锥EBCD的体积．【

答案】（1）证明见解析；（2）13．【解析】（1）证明：由ABBC，D为线段AC的中点，可得BDAC，由PAAB，PABC，ABBCB，可得PA平面ABC，又BD平面ABC，可得PABD，又PAACA

所以BD平面PAC，BD平面BDE，所以平面BDE平面PAC；（2）解：//PA平面BDE，PA平面PAC，且平面PAC平面BDEDE，可得//PADE，又D为AC的中点，可得E为PC的中点，且112DEPA

，由PA平面ABC，可得DE平面ABC，可得111221222BDCABCSS，则三棱锥EBCD的体积V=11111333BDCDES．2．（2021·全国高一课时练习）在四棱锥PABCD中，底面ABCD为矩形，AP平

面PCD，E，F分别为PC，AB的中点求证：（1）平面PAD平面ABCD；（2）//EF平面PAD【答案】（1）证明见解析；（2）证明见解析.【解析】证明：（1）∵AP平面PCD，CD平面PCD∴APCD∵ABCD为矩形，∴ADCD又：APADA，AP平面

PAD，AD平面PAD∴CD平面PAD∵CD平面ABCD∴平面PAD平面ABCD（2）连接AC，BD交于点O，连接OE，OF，∵ABCD为矩形，∴O点为AC中点∵E为PC中点∴//OEPA∵OE平面PAD，PA平面PAD∴//OE平面PAD同理可得：//OF平面PAD

∵OEOFO∴平面//OEF平面PAD∵EF平面OEF∴//EF平面PAD3．（2021·全国高一课时练习）如图所示，已知在三棱锥ABPC中，,APPCACBC，M为AB的中点，D为PB的中点，且PMB△为正三角

形．（Ⅰ）求证：//DM平面APC；（Ⅱ）求证：平面ABC平面APC；（Ⅲ）若4,20BCAB，求三棱锥DBCM的体积．【答案】（1）见详解；（2）见详解；（3）107【解析】证明：因为M为AB的中点，D为PB的中点，所以MD是ABP△的中位线，MDAPP.又MDË平面APC

，AP平面APC，所以MDP平面APC.（2）证明：因为PMB△为正三角形，D为PB的中点，所以MDPB.又MDAPP，所以APPB.又因为APPC，PBPCP＝，所以AP平面PBC.因为BC平面PBC，

所以APBC.又因为BCAC，ACAPA＝，所以BC⊥平面APC.(3)因为AP平面PBC，MDAPP，所以MD平面PBC，即MD是三棱锥MDBC的高.因为20AB，M为AB的中点，PMB△为正三角形，所以3

10,532PBMBMDMB.由BC⊥平面APC，可得BCPC，在直角三角形PCB中，由104PBBC＝，＝，可得221PC＝.于是1114221221222BCDBCPSS△△＝＝.112215310733DBCMMDBCBCDVVSMDg△＝＝＝考法四空

间距离【例4】（2020·全国专题练习）在棱长为a的正方体1111ABCDABCD中求出下列距离：（1）点A到面11BBCC的距离；（2）线段11BD到面ABCD的距离；（3）点A到面11BBDD的距离；（4）C到平面1BDC的距离.【答案】（1）a；（2）a

；（3）22a；（4）33a.【解析】（1）因为正方体1111ABCDABCD，则AB平面11BBCC，所以点A到面11BBCC的距离为边长ABa=；（2）因为11BD∥平面ABCD，且1BB平面ABCD，所以线段11BD

到面ABCD的距离为1BBa；（3）因为AC平面11BBDD，所以点A到面11BBDD的距离为面对角线的AC的12，即22a；（4）设C到平面1BDC的距离为h，三棱锥1CBDC的体积为V，在1BDC中，112BDDCBCa

，则1BDC的面积为2233(2)42aa，利用等体积法可得：211133232Vaaaah，所以33ha【一隅三反】1．（2020·北京二十中高一期末）如图，正四棱锥PABCD的高为2，且底面边长也为2，

则点A到平面PBC的距离为（）A．455B．255C．54D．52【答案】A【解析】由正四棱锥的性质可知，其底面ABCD为正方形，连接AC、BD，设交点为点O，连接PO，则PO平面ABCD，且2PO，底面对角线的长度为BD222222，侧棱长度

为PB22226，斜高22(6)15PM，1114·2223323PABCABCVSPO，1125522PBCSBCPM，设点A到平面PBC的距离为h，由APBCPABC

VV，即14533h，解得455h．故选：A.2．（2020·全国）已知正四棱柱ABCD-A1B1C1D1中，AB=2，CC1=22E为CC1的中点，则直线AC1与平面BED的距离为A．2

B．3C．2D．1【答案】D【解析】因为线面平行，所求求线面距可以转化为求点到面的距离，选用等体积法．1//AC平面BDE，1AC到平面BDE的距离等于A到平面BDE的距离，由题计算得111112222232323EABDABDVSCC，在BDE中，22226,22BED

EBD，BD边上的高22622，所以1222222BDES，所以112233ABDEBDEVShh，利用等体积法ABDEEABDVV，得:1222233h,解得:1h3．（2020·全国高一课时练习）已知

1111ABCDABCD是长方体，且4AB，3AD，12AA.（1）写出点A到平面11BCCB的距离；（2）写出直线AB到平面1111DCBA的距离；（3）写出平面11ADDA与平面11BCCB之间的距离.【答案】（1）4（2）2（3）4【

解析】如图.（1）点A到平面11BCCB的距离14hAB；（2）∵AB∥平面1111DCBA，∴AB到平面1111DCBA的距离212hAA；（3）∵平面11ADDA∥平面11BCCB，∴平面11ADDA与平面11BCCB之间的距离34

hAB.