【文档说明】人教版高中数学选择性必修第二册专题5.1《导数的概念及其意义、导数的运算》基础卷(原卷版).doc，共(3)页，283.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-37933.html

以下为本文档部分文字说明：

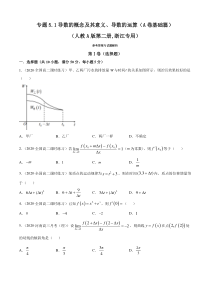
专题5.1导数的概念及其意义、导数的运算（A卷基础篇）（人教A版第二册,浙江专用）参考答案与试题解析第Ⅰ卷（选择题）一．选择题（共10小题，满分50分，每小题5分）1．（2020·全国高二课时练习）甲

、乙两厂污水的排放量W与时间t的关系如图所示，则治污效果较好的是（）A．甲厂B．乙厂C．两厂一样D．不确定2．（2020·全国高二课时练习）若000lim1xfxmxfxx（m为常数），则0fx等于（）A．mB．1C．mD．1m3．（2020·全国高二课时练习）某质

点的运动规律为23st，则在时间(3,3)t内，质点的位移增量等于（）A．26()ttB．96ttC．23()ttD．9t4．（2020·全国高二课时练习）已知2xfxxe，则0f（）A．

0B．4C．2D．15．（2020·河南高三月考（理））设022lim2xfxfxx，则曲线yfx在点22f,处的切线的倾斜角是（）A．4B．3C．34D．236．（2020·北京高二期末）已知函数yfx在0

xx处的导数为1，则000lim2xfxxfxx（）A．0B．12C．1D．27．（2020·安徽省蚌埠第三中学高二月考（理））过原点作曲线lnyx的切线，则切线的斜率为（）A．eB．1eC．1D．21e8．（2018·广东高二期末（理））曲线2yxx

在点(1,2)P处切线的斜率为（）A．1B．2C．3D．49．（2020·全国高二单元测试）下列导数运算正确的是（）A．122xxxB．(sincos1)cos2xxxC．1(lg)xx

D．12xx10．（2020·北京海淀区·人大附中高二期末）曲线421yxax在点(1,2)a处的切线斜率为8，则实数a的值为（）A．6B．6C．12D．12第Ⅱ卷（非选择题）二．填空题（共7小题，单空每小题4分，两空每小题6分，共36分）11．

（2020·贵溪市实验中学高三月考（文））曲线ln2yxxx在点（1，2）处的切线方程为_________.12．（2020·广东广州市·华南师大附中高三月考（文））曲线sin2cosyxx在点,2处的切线方程为_____.13．（2020·安徽淮北市·淮北一中高二

期中）已知2()21fxxxf，则1f等于__________.（用数字作答）14．（2020·全国高二单元测试）已知曲线y＝x2－1上两点A(2,3)，B(2＋Δx,3＋Δy)，当Δx＝1时，割线AB的斜率是________；当Δx＝0.1时，割线

AB的斜率是________．15．（2012·全国高二课时练习）函数32()2354fxxxx的导数()fx_______________________，(3)f___________.1

6．（2020·宁波市北仑中学高二期中）已知函数2xfx，则fx__________，设1gxgfxx，则1g_________．17．（2020·浙江高三其他模拟）德国数学家莱布尼茨是微

积分的创立者之一，他从几何问题出发，引进微积分概念．在研究切线时，他将切线问题理解为“求一条切线意味着画一条直线连接曲线上距离无穷小的两个点”，这也正是导数定义的内涵之一．现已知直线yxb是函数()lnfxx的切线，也是函数()xkgxe的切线，则实数b____，

k_____．三．解答题（共5小题，满分64分，18--20每小题12分，21,22每小题14分）18．（2020·日喀则市第三高级中学高二期末（文））（1）求导：33cos243lnxyxxx（2）求函数lnyxx在1x处的导数.19．（2020·北京市房

山区房山中学高二期中）32fxaxbxcxd，且03f，00f，13f，20f；求abcd,,,的值．20．（2020·全国高三专题练习（文））已知P（﹣1，1），Q（2，4）是曲线y=x2上的两点，求与直线PQ平行且与曲线

相切的切线方程．21．（2020·海林市朝鲜族中学高二期末（文））已知函数()(1)xfxxeax的图像在0x处的切线方程是0xyb，求a，b的值；22．（2020·全国高二课时练习）求曲线2

1xye在点(0,2)处的切线与直线0y和yx围成的三角形的面积.