【文档说明】高考数学(文数)一轮复习课件 第六章 不等式、推理与证明 第五节 合情推理与演绎推理(含详解).ppt，共(20)页，459.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-33621.html

以下为本文档部分文字说明：

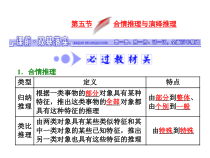
第五节合情推理与演绎推理类型定义特点归纳推理根据一类事物的____对象具有某种特征，推出这类事物的____对象都具有这种特征的推理由____到____、由____到____类比推理由两类对象具有某些类似特征和其中一类对象的某些已知特征，推出另一类对象也具有这些特征的

推理由____到____部分全部部分整体个别一般特殊特殊1．合情推理2．演绎推理(1)定义：从一般性的原理出发，推出某个特殊情况下的结论，我们把这种推理称为演绎推理．简言之，演绎推理是由一般到的推理．(2)“三段论”是演绎推理的一般模式，包括：①大

前提——已知的一般原理；②小前提——所研究的特殊情况；③结论——根据一般原理，对特殊情况做出的判断．特殊1．(教材习题改编)已知数列{an}的第1项a1＝1，且an＋1＝an1＋an(n＝1,2,3，„)，归纳该数列的通项公式an＝________．答案：1n[小题体验]2．(教

材习题改编)在平面上，若两个正三角形的边长的比为1∶2，则它们的面积比为1∶4．类似地，在空间中，若两个正四面体的棱长的比为1∶2，则它们的体积比为________．答案：1∶81．合情推理是从已知的结论推测未知的结论，发现与猜想的结论都要经过进一步严格证明．2．演绎推理是由一般到特殊

的证明，它常用来证明和推理数学问题，注意推理过程的严密性，书写格式的规范性．3．合情推理中运用猜想不能凭空想象，要有猜想或拓展依据．判断正误(请在括号中打“√”或“×”)．(1)归纳推理得到的结论不一定正确，类比推理得到的结论一定正确()(2)由平面三角形的性质推测空间四面体的性质，这是一种合

情推理()(3)在类比时，平面中的三角形与空间中的平行六面体作为类比对象较为合适()(4)在演绎推理中，只要符合演绎推理的形式，结论就一定正确()×[小题纠偏]√××考点一类比推理[题组练透]1．给出下面类比推理(其中Q为有理数集，R为实数集，C为复数集)：①“若a，b∈R，则a－b＝0⇒a＝b”

类比推出“a，c∈C，则a－c＝0⇒a＝c”；②“若a，b，c，d∈R，则复数a＋bi＝c＋di⇒a＝c，b＝d”类比推出“a，b，c，d∈Q，则a＋b2＝c＋d2⇒a＝c，b＝d”；③“a，b∈R，则a－b＞0⇒a＞b”类比推出

“若a，b∈C，则a－b＞0⇒a＞b”；④“若x∈R，则|x|＜1⇒－1＜x＜1”类比推出“若z∈C，则|z|＜1⇒－1＜z＜1”．其中类比结论正确的个数为()A．1B．2C．3D．4解析：类比结论正确的有①②．答案：B2．若P0(x0，y0)在椭圆x2a2＋

y2b2＝1(a＞b＞0)外，过P0作椭圆的两条切线的切点为P1，P2，则切点弦P1P2所在的直线方程是x0xa2＋y0yb2＝1，那么对于双曲线则有如下命题：若P(x0，y0)在双曲线x2a2－y2b2＝1(a＞0

，b＞0)外，过P0作双曲线的两条切线，切点为P1，P2，则切点弦P1P2所在直线的方程是________．解析：类比椭圆的切点弦方程可得双曲线x2a2－y2b2＝1的切点弦方程为x0xa2－y0yb2＝1．答案：x0xa2－y0y

b2＝1[谨记通法]类比推理的分类及处理方法类别解读适合题型类比定义在求解由某种熟悉的定义产生的类比推理型试题时，可以借助原定义来求解已知熟悉定义类比新定义类比性质从一个特殊式子的性质、一个特殊图形的性质入手，提出

类比推理型问题，求解时要认真分析两者之间的联系与区别，深入思考两者的转化过程是求解的关键平面几何与立体几何、等差数列与等比数列类比方法有一些处理问题的方法具有类比性，可以把这种方法类比应用到其他问题的求解中，注意

知识的迁移已知熟悉的处理方法类比未知问题的处理方法考点二归纳推理归纳推理是每年高考的常考内容，题型多为选择题和填空题，难度稍大，属中高档题．常见的命题角度有：(1)与数字有关的推理；(2)与式子有关的推理；

(3)与图形有关的推理．[锁定考向][题点全练]角度一：与数字有关的推理1．(2016·甘肃两市三校3月联考)观察下列等式：1＝12＋3＋4＝93＋4＋5＋6＋7＝254＋5＋6＋7＋8＋9＋10＝49„„照此规律，第n个等式为__________________

______．解析：由前4个等式可知，第n个等式的左边第一个数为n，且连续2n－1个整数相加，右边为(2n－1)2，故第n个等式为n＋(n＋1)＋(n＋2)＋„＋(3n－2)＝(2n－1)2．答案：n＋(n＋1)＋(n＋2)＋„＋(3n－2)＝(2n－1)2角度

二：与式子有关的推理2．已知f(x)＝x1＋x，x≥0，若f1(x)＝f(x)，fn＋1(x)＝f(fn(x))，n∈N*，则f2017(x)的表达式为____________．解析：f1(x)＝x1＋x

，f2(x)＝x1＋x1＋x1＋x＝x1＋2x，f3(x)＝x1＋2x1＋x1＋2x＝x1＋3x，„，归纳可得f2017(x)＝x1＋2017x．答案：f2017(x)＝x1＋2017x．角度三：与图形有关的推理

3．下面图形由小正方形组成，请观察图1至图4的规律，并依此规律，写出第n个图形中小正方形的个数是________．解析：由题图知第n个图形的小正方形个数为1＋2＋3＋„＋n．∴总个数为nn＋12．答案：nn＋12[通法在握]归纳推理

问题的常见类型及解题策略常见类型解题策略与数字有关的等式的推理观察数字特点，找出等式左右两侧的规律及符号可解与式子有关的推理观察每个式子的特点，找到规律后可解与图形变化有关的推理合理利用特殊图形归纳推理得出结论，并用赋值检验法验证其真伪性[演练冲关]1．(2017·贵

阳监测)已知不等式1＋14＜32，1＋14＋19＜53，1＋14＋19＋116＜74，照此规律总结出第n(n∈N*)个不等式为________．解析：由已知，三个不等式可以写成1＋122＜2×2－12，1＋122＋132＜2×3－13，1＋

122＋132＋142＜2×4－14，所以照此规律可得到第n个不等式为1＋122＋132＋„＋1n2＋1n＋12＜2n＋1－1n＋1＝2n＋1n＋1．答案：1＋122＋132＋„＋1n2＋1n＋12＜2n＋1n＋12．某种平面分形图如图所示，一级分形图是由一点出发的三条线段，长度均

为1，两两夹角为120°；二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来13的线段，且这两条线段与原线段两两夹角为120°，„，依此规律得到n级分形图．n级分形图中共有________条线段．解析：分形图的每条线段的末端出发再生成两条线段，由题图知，一级分形图有3＝(3×2－3)

条线段，二级分形图有9＝(3×22－3)条线段，三级分形图中有21＝(3×23－3)条线段，按此规律n级分形图中的线段条数an＝3×2n－3．答案：3×2n－3考点三演绎推理[典例引领]数列{an}的前n项和记为Sn，已知a1＝1，an＋1＝n＋

2nSn(n∈N*)．证明：(1)数列Snn是等比数列；(2)Sn＋1＝4an．证明：(1)∵an＋1＝Sn＋1－Sn，an＋1＝n＋2nSn，∴(n＋2)Sn＝n(Sn＋1－Sn)，即nSn＋1＝2(n

＋1)Sn．故Sn＋1n＋1＝2·Snn，(小前提)故Snn是以2为公比，1为首项的等比数列．(结论)(大前提是等比数列的定义)(2)由(1)可知Sn＋1n＋1＝4·Sn－1n－1(n≥2)，∴Sn＋1＝4(n＋1)·Sn－1n

－1＝4·n－1＋2n－1·Sn－1＝4an(n≥2)．(小前提)又∵a2＝3S1＝3，S2＝a1＋a2＝1＋3＝4＝4a1，(小前提)∴对于任意正整数n，都有Sn＋1＝4an．(结论)[由题悟法]演绎推理的推证规则(1)演绎推理是从一般到特殊的推理

，其一般形式是三段论，应用三段论解决问题时，应当首先明确什么是大前提和小前提，如果前提是显然的，则可以省略，本题中，等比数列的定义在解题中是大前提，由于它是显然的，因此省略不写．(2)在推理论证过程中，一些稍复杂一点的证明题

常常要由几个三段论才能完成．[即时应用]已知函数y＝f(x)满足：对任意a，b∈R，a≠b，都有af(a)＋bf(b)>af(b)＋bf(a)，试证明：f(x)为R上的单调增函数．证明：设x1，x2∈R，取x1<x2，则由题意

得x1f(x1)＋x2f(x2)>x1f(x2)＋x2f(x1)，∴x1[f(x1)－f(x2)]＋x2[f(x2)－f(x1)]>0，[f(x2)－f(x1)](x2－x1)>0，∵x1<x2，∴f(x2)－f(x1)>0，f(

x2)>f(x1)．∴y＝f(x)为R上的单调增函数．