【文档说明】2021年人教版高中数学必修第二册(精练)第八章《知识总结及测试》（原卷版）.doc，共(11)页，909.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-39080.html

以下为本文档部分文字说明：

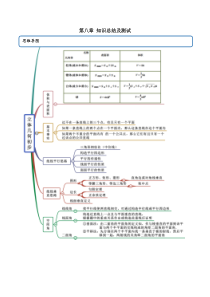
第八章知识总结及测试思维导图一、单选题（每题5分，8题共40分）1．（2020·全国高一课时练习）如图所示，观察四个几何体，其中判断正确的是（）单元测试A．①是棱台B．②是圆台C．③是四面体D．④不是棱柱2．（2020·全国高一课

时练习）已知两个平面相互垂直，下列命题①一个平面内已知直线必垂直于另一个平面内的任意一条直线②一个平面内已知直线必垂直于另一个平面内的无数条直线③一个平面内任意一条直线必垂直于另一个平面④过一个平面内任意一点作交

线的垂线，则此垂线必垂直于另一个平面其中正确命题个数是（）A．1B．2C．3D．43．（2021·全国高一）已知三条不同的直线,,lmn和两个不同的平面,，下列四个命题中正确的是（）A．若//,//mn，则//mnB．若/

/,lm，则//lmC．若,l，则lD．若//,ll，则4．（2020·全国高一课时练习）已知正三棱柱111ABCABC，O为ABC的外心，则异面直线1AC与OB所成角的大小为（）A．30°B．60°C．45°D．90°5．（2020·全国高一课时练习）

已知三棱锥PABC，面PAB面ABC，4PAPB，43AB，90ACB，则三棱锥PABC外接球的表面积（）A．20B．32C．64πD．806．（2020·青铜峡市高级中学）如图所示，AB是⊙O的直径，VA垂直于⊙O所在的平面，点C是圆周上不同于A，

B的任意一点，M，N分别为VA，VC的中点，则下列结论正确的是（）A．MN//ABB．MN与BC所成的角为45°C．OC平面VACD．平面VAC平面VBC7．（2020·全国高一课时练习）已知正四面体ABCD的表面积为S，其四个面的中心分别为,

,,EFGH，设四面体EFGH的表面积为T，则TS等于（）A．19B．49C．14D．138．（2020·四川省资中县第二中学）古希腊数学家阿基米德是世界上公认的三位最伟大的数学家之一，其墓碑上刻着他认为最满意的一个数学发现，如图，一个“圆柱容球”的几何图形，即圆柱容器里放了一个球，该球顶天立地

，四周碰边，在该图中，球的体积是圆柱体积的23，并且球的表面积也是圆柱表面积的23，若圆柱的表面积是6π现在向圆柱和球的缝隙里注水，则最多可以注入的水的体积为（）A．2B．23C．πD．43二、多选题（

每题不止一个选择为正确答案，每题5分，4题共20分）9．（2020·广东汕头市·金山中学）已知直三棱柱111ABCABC中，ABBC，1ABBCBB，D是AC的中点，O为1AC的中点.点P是1BC上的动点，则下列说法正确的是（）A．当点P运动

到1BC中点时，直线1AP与平面111ABC所成的角的正切值为55B．无论点P在1BC上怎么运动，都有11APOBC．当点P运动到1BC中点时，才有1AP与1OB相交于一点，记为Q，且113PQQAD．无论

点P在1BC上怎么运动，直线1AP与AB所成角都不可能是30°10．（2020·全国）下列四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形是（）A．B．C．D．11．（2020·平潭县新世纪学校）已知正方体ABCD﹣A1B1C

1D1的棱长为1，E是DD1的中点，则下列选项中正确的是（）A．AC⊥B1EB．B1C∥平面A1BDC．三棱锥C1﹣B1CE的体积为13D．异面直线B1C与BD所成的角为45°12．（2020·全国高一课时练习）如图，

在正方形ABCD中，E，F分别是BC，CD的中点，G是EF的中点.现在沿AE，AF及EF把这个正方形折成一个空间图形，使B，C，D三点重合，重合后的点记为H，下列说法正确的是（）A．AG⊥平面EFHB．AH⊥平面EFHC．HF⊥平面AEHD．HG⊥平面AE

F三、填空题（每题5分，4题共20分）13．（2021·山东高三专题练习）如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2cm，高为2cm，内孔半径为0.5cm，则此六角螺帽毛坯的体积

是____cm.14．（2021·浙江高一期末）如图，点E是正方体1111ABCDABCD的棱1DD的中点，点M在线段1BD上运动，则下列结论正确的有__________．①直线AD与直线1CM始终是异面直线②存在点M，使得1B

MAE③四面体EMAC的体积为定值④当12DMMB时，平面EAC平面MAC3．（2021·浙江绍兴市·高二期末）如图，已知直四棱柱1111ABCDABCD的所有棱长均相等，3BAD，E是棱AB的中点，设平面经过直线1AE，且平面111,BBCCl平面112C

CDDl，若平面11AACC，则异面直线1l与2l所成的角的余弦值为_______．16．（2021·黑龙江哈尔滨市·哈尔滨三中）已知四棱锥PABCD的底面ABCD是矩形，其中1,2ADAB，侧棱PA底面ABCD，且直线P

B与CD所成角的余弦值为255，则四棱锥PABCD的外接球表面积为___________.四、解答题（第17题10分，其余每题12分，共70分）17．（2020·全国高一课时练习）如图，四棱锥P﹣ABCD的底面ABCD为菱形，PB＝PD，E，F分别为A

B和PD的中点.（1）求证：EF∥平面PBC；（2）求证：平面PBD⊥平面PAC．18．（2020·山东菏泽市·菏泽一中高一月考）如图，在四棱锥P-ABCD中，底面ABCD为正方形，侧面PAD是正三角形，侧面PAD底面ABCD，M是PD的中点.（1）求证：AM平面PCD；（2）求侧面PBC与

底面ABCD所成二面角的余弦值.3．（2020·盘锦市第二高级中学高二月考）如图，在三棱锥P-ABC中，90ACB，PA底面ABC.（1）求证：平面PAC平面PBC；（2）若ACBCPA

，M是PB的中点，求AM与平面PBC所成角的正切值.20．（2020·全国高一课时练习）如图，在边长为2的正方形ABCD中，点E是AB的中点，点F是BC的中点，将,,AEDBEFDCF分别沿DE，EF，DF折起，使A，B，C三点重合于点A.（1）求证ADE

F;（2）求三棱锥AEFD的体积.21．（2021·浙江月考）已知四边形ABCD，90ABCCAD，22ABBCAD，将ABC沿AC翻折至PAC△.（Ⅰ）若PAPD，求证：APCD；（Ⅱ）若二面角PACD的余弦值为14，求PD与面PAC所

成角的正弦值.22．（2020·全国专题练习）如图，在长方体1111ABCDABCD中，1,2,,ABADEF分别为1,ADAA的中点，Q是BC上一个动点，且(0)BQQC.（1）当1时，求证：平面BEFP平面1ADQ；（2）是否存在

，使得BDFQ？若存在，请求出的值；若不存在，请说明理由.