【文档说明】2021年人教版高中数学必修第二册(精练)第八章《知识总结及测试》（解析版）.doc，共(26)页，1.746 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-39330.html

以下为本文档部分文字说明：

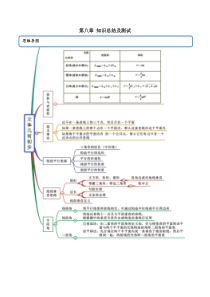
第八章知识总结及测试思维导图一、单选题（每题5分，8题共40分）1．（2020·全国高一课时练习）如图所示，观察四个几何体，其中判断正确的是（）单元测试A．①是棱台B．②是圆台C．③是四面体D．④不是棱柱【答案】C【解析】图①不是

由棱锥截来的，所以①不是棱台；图②上、下两个面不平行，所以②不是圆台；图③是四面体.图④前、后两个面平行，其他面是平行四边形，且每相邻两个四边形的公共边平行，所以④是棱柱.故选：C.2．（2020·全国高一课时练习）已知两个平面相互垂

直，下列命题①一个平面内已知直线必垂直于另一个平面内的任意一条直线②一个平面内已知直线必垂直于另一个平面内的无数条直线③一个平面内任意一条直线必垂直于另一个平面④过一个平面内任意一点作交线的垂线，则此垂线必垂直于另一个平面其中正确命题个数是（）A．1B

．2C．3D．4【答案】A【解析】由题意，对于①，当两个平面垂直时，一个平面内的不垂直于交线的直线不垂直于另一个平面内的任意一条直线，故①错误；对于②，设平面α∩平面β=m，n⊂α，l⊂β，∵平面α⊥平面β，∴当l⊥m时，必有l⊥α，而n⊂α，∴l⊥n，而在平面β内与l平

行的直线有无数条，这些直线均与n垂直，故一个平面内的已知直线必垂直于另一个平面内的无数条直线，即②正确；对于③，当两个平面垂直时，一个平面内的任一条直线不不一定垂直于另一个平面，故③错误；对于④，当两个平面垂直时，过一个平面内任意一点作交线的垂线，若该直线不在第一个平面内，则此直线

不一定垂直于另一个平面，故④错误；故选A．3．（2021·全国高一）已知三条不同的直线,,lmn和两个不同的平面,，下列四个命题中正确的是（）A．若//,//mn，则//mnB．若//,lm，则//lmC．若,l

，则lD．若//,ll，则【答案】D【解析】若//,//mn,可以有//mn或,mn相交，故A错；若//,lm，可以有//lm或lm、异面，故B错；若,l，可以有l、l与斜交、l//，故C错；过l作平面nI，

则//ln，又l，得n，n，所以，故D正确.故选:D4．（2020·全国高一课时练习）已知正三棱柱111ABCABC，O为ABC的外心，则异面直线1AC与OB所成角的大小为（）A．30°B．60°C．45°D．90°【答案】D【解析】

如图，ABC是等边三角形，且O为ABC的外心，O是ABC的垂心，BOAC，且1AA平面ABC，BO平面ABC，1BOAA，BO平面11AACC，且1AC平面11AACC，1BOAC，异面直线1AC与OB所成角的大小为90．故选：D．5．（2020·全国

高一课时练习）已知三棱锥PABC，面PAB面ABC，4PAPB，43AB，90ACB，则三棱锥PABC外接球的表面积（）A．20B．32C．64πD．80【答案】C【解析】如下图所示，取AB的中点D，连接PD、CD，4PAPB，D为AB

的中点，PDAB，平面PAB平面ABC，交线为AB，PD平面ABC，PD平面ABC，90ACB,D∴为RtABC外接圆圆心，则球心O在直线PD上，设三棱锥PABC外接球的半径为R，则2ODR

，43AB，则23AD，222PDPAAD，在RtOAD中，由勾股定理得222OAODAD，即22212RR，解得4R，因此，三棱锥PABC的外接球的表面积为2464R.故选：C.6．（2020·青铜峡市高级中学）如图所示，AB是⊙O的直径

，VA垂直于⊙O所在的平面，点C是圆周上不同于A，B的任意一点，M，N分别为VA，VC的中点，则下列结论正确的是（）A．MN//ABB．MN与BC所成的角为45°C．OC平面VACD．平面VAC平面VBC【答案】D【解析】M，N分别为

VA，VC的中点，在△VAC中有//MNAC，在面ABC中ABACA，MN不与AB平行；ACBCC，知：MN与BC所成的角为90BCA；因为OC面VACC，OC与平面内交线,ACVC都不垂直，OC不与平面VAC垂直；由VA面A

BC，BC面ABC即VABC，而90BCA知ACBC，ACVAA有BC面VAC，又BC面VBC，所以面VAC面VBC；故选：D7．（2020·全国高一课时练习）已知正四面体ABCD的表面积为S，其四个面的中心分别为,,,EFGH，设四面体EF

GH的表面积为T，则TS等于（）A．19B．49C．14D．13【答案】A【解析】如图所示，正四面体ABCD四个面的中心分别为E、F、G、H，四面体EFGH也是正四面体．连接AE并延长与CD交于点M，连接AG并延长与BC交于点N．E、

G分别为面的中心，23AEAGAMAN．23GEMN．又12MNBD，13GEBD．面积比是相似比的平方，两四面体的面积比为；19TS．故选：A．8．（2020·四川省资中县第二中学）古希腊数学家阿基米德

是世界上公认的三位最伟大的数学家之一，其墓碑上刻着他认为最满意的一个数学发现，如图，一个“圆柱容球”的几何图形，即圆柱容器里放了一个球，该球顶天立地，四周碰边，在该图中，球的体积是圆柱体积的23，并且球的表面积也是圆柱表面积的23，若圆柱的表面积是6π现在向圆柱和球的缝隙里注水，则最多可以

注入的水的体积为（）A．2B．23C．πD．43【答案】B【解析】设球的半径为r，则由题意可得球的表面积为22463r，所以r＝1，所以圆柱的底面半径为1，高为2，所以最多可以注入的水的体积为234212133.故选：B.二、多选题（每题不

止一个选择为正确答案，每题5分，4题共20分）9．（2020·广东汕头市·金山中学）已知直三棱柱111ABCABC中，ABBC，1ABBCBB，D是AC的中点，O为1AC的中点.点P是1BC上的动点，则下列说法正确的是（）A．当点P运动到1BC中点时，直线1AP与平面111ABC所成的角

的正切值为55B．无论点P在1BC上怎么运动，都有11APOBC．当点P运动到1BC中点时，才有1AP与1OB相交于一点，记为Q，且113PQQAD．无论点P在1BC上怎么运动，直线1AP与AB所成角都不可能是30°【答案】ABD【解析】直三棱柱111ABCABC中，

ABBC，1ABBCBB选项A中，当点P运动到1BC中点时，有E为11BC的中点，连接1AE、EP，如下图示即有EP面111ABC∴直线1AP与平面111ABC所成的角的正切值：1tanEPPAEAE∵112EPBB

，22111152AEABBEBB∴15tan5PAE，故A正确选项B中，连接1BC，与1BC交于E，并连接1AB，如下图示由题意知，11BBCC为正方形，即有11BCBC而ABBC且111ABCABC为直三棱柱，有11AB面11BBCC，1BC面11BBCC∴

111ABBC，又1111ABBCB∴1BC面11ABC，1OB面11ABC，故11BCOB同理可证：11ABOB，又11ABBCB∴1OB面11ABC，又1AP面11ABC，即有11APOB，故B正确选项C中，点P运动到1BC中点时，即在△11ABC中1AP、

1OB均为中位线∴Q为中位线的交点∴根据中位线的性质有：112PQQA，故C错误选项D中，由于11//ABAB，直线1AP与AB所成角即为11AB与1AP所成角：11BAP结合下图分析知：点P在1BC

上运动时当P在B或1C上时，11BAP最大为45°当P在1BC中点上时，11BAP最小为23arctanarctan3023∴11BAP不可能是30°，故D正确故选：ABD10．（2020·全国）

下列四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形是（）A．B．C．D．【答案】AD【解析】在A中，连接AC，则AC∥MN，由正方体性质得到平面MNP∥平面ABC，∴AB∥平面MNP，故A成立；对于B，若下底面

中心为O，则NO∥AB，NO∩面MNP＝N，∴AB与面MNP不平行，故B不成立；对于C，过M作ME∥AB，则E是中点，则ME与平面PMN相交，则AB与平面MNP相交，∴AB与面MNP不平行，故C不成立；对于D，连接CE，则AB∥CE，NP∥CD，则AB∥PN，∴AB∥平面MNP，故D成

立.故选：AD.11．（2020·平潭县新世纪学校）已知正方体ABCD﹣A1B1C1D1的棱长为1，E是DD1的中点，则下列选项中正确的是（）A．AC⊥B1EB．B1C∥平面A1BDC．三棱锥C1﹣B1CE的体积为13D．异面直线B1

C与BD所成的角为45°【答案】AB【解析】如图，∵AC⊥BD，AC⊥BB1，∴AC⊥平面BB1D1D，又B1E⊂平面BB1D1D，∴AC⊥B1E，故A正确；∵B1C∥A1D，A1D⊂平面A1BD，B1C平面

A1BD，∴B1C∥平面A1BD，故B正确；三棱锥C1﹣B1CE的体积为111111111326CBCEBCCEVV，故C错误；∵BD∥B1D1，∴∠CB1D1是异面直线B1C与BD所成的角，又△CB1D1是等边三角形，∴异面直线B1C与BD所成的角为60°，

故D错误.故选：AB.12．（2020·全国高一课时练习）如图，在正方形ABCD中，E，F分别是BC，CD的中点，G是EF的中点.现在沿AE，AF及EF把这个正方形折成一个空间图形，使B，C，D三点重合，重合后的点记为H，下列说法正确的是（

）A．AG⊥平面EFHB．AH⊥平面EFHC．HF⊥平面AEHD．HG⊥平面AEF【答案】BC【解析】由题意可得：AH⊥HE，AH⊥HF.∴AH⊥平面EFH，而AG与平面EFH不垂直.∴B正确，A不正确.又HF⊥HE，∴HF⊥平面AHE，C正确.HG与AG不

垂直，因此HG⊥平面AEF不正确.D不正确.故选：BC.三、填空题（每题5分，4题共20分）13．（2021·山东高三专题练习）如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2cm，高为2cm，内孔半径为0

.5cm，则此六角螺帽毛坯的体积是____cm.【答案】1232【解析】正六棱柱体积为23622=1234圆柱体积为21()222所求几何体体积为1232故答案为：123214．（2

021·浙江高一期末）如图，点E是正方体1111ABCDABCD的棱1DD的中点，点M在线段1BD上运动，则下列结论正确的有__________．①直线AD与直线1CM始终是异面直线②存在点M，使得1BMAE③四面体EMAC的体积为定值④当12D

MMB时，平面EAC平面MAC【答案】②③④.【解析】对于①：连接1AC交1BD于点O，当点M在O点时直线AD与直线1CM相交，故①不正确，以D为坐标原点，建立如图所示的空间直角坐标系，设正方体的边长为2，则0,0,0D，

10,0,2D，2,0,0A，0,2,0C，0,0,1E，2,2,0B，12,2,2B，对于②：2,0,1AE，假设存在点M，使得1BMAE，1110,0,22,2,22,2,22BMBBBD，0,1

，所以14220AEBM，解得13，所以当12DMMB时1BMAE，故②正确；对于③：连接AC、BD交于点1O，因为点E是棱1DD的中点，此时11//EOBD，故线段1BD到平面AEC的距离为定值，所以四面体EMAC的体积为定值，故③正确；对于④：当12DMMB

时，442,,333M，2,0,1AE，2,2,0AC，设平面AEC的法向量为111,,mxyz，由111120220mAExzmACxy令12z，可得11x，11y，可得1,1,2m，设平面MAC的法向量为

222,,nxyz，242,,333MA，由222222202420333nACxynMAxyz解得:20y，令21x可得22z，所以()1,1,1n=-，因为111

1120mn，mn所以平面EAC平面MAC，故④正确；故答案为：②③④.3．（2021·浙江绍兴市·高二期末）如图，已知直四棱柱1111ABCDABCD的所有棱长均相等，3BAD，E是棱AB的中点，设平面经过直线1AE，且平面111,B

BCCl平面112CCDDl，若平面11AACC，则异面直线1l与2l所成的角的余弦值为_______．【答案】910【解析】由直四棱柱1111ABCDABCD的所有棱长均相等，3BAD，所以ABCD

是菱形，连接ACBD、，1111ACBD、，且ACBDO，11111ACBDO，所以BDAC，1111BDAC，因为1AA平面ABCD，BD平面ABCD，所以1AABD，且1AAACA，所以BD平面11AACC，取AD的中点F，连接1AF，连接EF交

AC与G，所以//EFBD，且G是AO的中点，所以EF平面11AACC，所以平面1AEF平面11AACC，又1AE平面1AEF，所以平面1AEF即平面，分别取1111BCDC、的中点MN、，连接MN交11AC与H点，H即为11OC的中点，所以1AHGC，且1//AHGC，所

以四边形1AHCG是平行四边形，所以1//AGHC，1AG平面CMN，CH平面CMN，所以//AG平面CMN，又因为11//////EFBDBDMN，EF平面CMN，MN平面CMN，所以//MN平面CMN，又1AGEFG，所以

平面1//AEF平面MNC，且平面11BCCB平面MNCMC，平面11DCCD平面MNCNC，所以//CM1l，//CN2l，所以异面直线1l与2l所成的角即CM与CN所成的角，设2AB，则直四棱柱1111ABCD

ABCD的所有棱长均为2，由3BAD，所以112BDABBD，11112MNDB，且2211415CMCNCCCM，由余弦定理得222551922510CMCNMNMCNCMCN.故答案为：910.16．（2021·黑龙江哈尔滨

市·哈尔滨三中）已知四棱锥PABCD的底面ABCD是矩形，其中1,2ADAB，侧棱PA底面ABCD，且直线PB与CD所成角的余弦值为255，则四棱锥PABCD的外接球表面积为___________.【答案】6【解析

】如图，因为//ABCD，故PBA或其补角为异面直线PB与CD所成的角，因为PA平面ABCD，ABÌ平面ABCD，故PAAB，故PBA为锐角，故25cos5PBA，故25255PB，故1PA.将该四棱锥补成如图所示的长方体：则该长方体的外接球即为四棱锥的外

接球，其直径为1146，故表面积为22426RR.故答案为：6.四、解答题（第17题10分，其余每题12分，共70分）17．（2020·全国高一课时练习）如图，四棱锥P﹣ABCD的底面ABCD为菱形，PB＝PD，E，F分别为AB和PD的中点.（1）求证：

EF∥平面PBC；（2）求证：平面PBD⊥平面PAC．【答案】（1）证明见解析；（2）证明见解析.【解析】证明：（1）取PC的中点G，连接FG，BG，如图所示：∵F是PD的中点，∴FG∥CD，且12FGCD，又∵底面ABCD是菱形，E是AB中点，

∴BE∥CD，且12BECD，∴BE∥FG，且BE＝FG，∴四边形BEFG是平行四边形，∴EF∥BG，又EF⊄平面PBC，BG⊂平面PBC，∴EF∥平面PBC；（2）设AC∩BD＝O，则O是BD中点，连接PO，∵底面ABCD是菱形，∴BD⊥AC，又∵PB＝PD，O是BD中点，∴BD⊥PO，又AC

∩PO＝O，AC⊂平面PAC，PO⊂平面PAC，∴BD⊥平面PAC，∵BD⊂平面PBD，∴平面PBD⊥平面PAC.18．（2020·山东菏泽市·菏泽一中高一月考）如图，在四棱锥P-ABCD中，底面ABCD为正方形，侧面PAD是正三角形，侧面PAD底面ABCD，M是PD的中点.

（1）求证：AM平面PCD；（2）求侧面PBC与底面ABCD所成二面角的余弦值.【答案】（1）见解析；（2）277【解析】（1）在正方形ABCD中，CDAD，又侧面PAD底面ABCD，侧面PAD底面ABCDAD，所

以CD平面PAD，AM平面PAD，所以CDAM，PADQV是正三角形，M是PD的中点，所以AMPD，又CDPDD，所以AM平面PCD.（2）取AD，BC的中点分别为E，F，连接EF，PE，PF，则

,//EFCDEFCD，所以EFAD，又在正PAD中，PEAD，,EFPEEAD平面PEF，∵正方形ABCD中，//,ADBCBC平面PEF，PFE是侧面PBC与底面ABCD所成二面角的平面角，由CD平面PAD，//EFCD，EF平面PEF，PE

Q平面PAD，EFPE.设正方形ABCD的边长2ADa，则2,3EFaPEa，所以227PFPEEFa，所以27cos7EFPFEPF,即侧面PBC与底面ABCD所成二面角的余弦值为277.3．（2020·盘锦市第二高级中学高二月考）如图，在三棱锥P-ABC中，90

ACB，PA底面ABC.（1）求证：平面PAC平面PBC；（2）若ACBCPA，M是PB的中点，求AM与平面PBC所成角的正切值.【答案】（1）见解析；（2）2【解析】（1）由题意，因为PA面ABC，BC面ABC，PABC，又90ACB，即ACB

C，PAACAQI，BC平面PAC，BC平面PBC，∴平面PAC平面PBC.（2）取PC的中点D，连接AD，DM.,ACPAADPC.由（1）知，BC⊥平面PAC，又AD平面PAC，BCAD.而PCBCC

.AD平面PBC，所以DM是斜线AM在平面PBC上的射影，所以AMD∠是AM与平面PBC所成角，且ADDM，设2ACBCPAa，则由M是PB中点得12DMBCa，2ADa，所以tan2ADAMDDM，即AM与平面PBC所成角的正切值为2.20．（2020·全国高一课时练

习）如图，在边长为2的正方形ABCD中，点E是AB的中点，点F是BC的中点，将,,AEDBEFDCF分别沿DE，EF，DF折起，使A，B，C三点重合于点A.（1）求证ADEF;（2）求三棱锥AEFD的体积.【答案】

（1）见解析；（2）13【解析】（1）由题意，根据折叠前后，可得,ADAEADAF，又AEAFA，所以AD平面AEF，又由EF平面AEF，所以ADEF（2）由（1）可知，AD平面

AEF，所以三棱锥DAEF的高2ADAD，又AEF折前为BEF，E，F分别为AB，BC的中点，所以'111122AEFBEFSS，所以'''111123323AEFSDAEFAEFVVSA

D.21．（2021·浙江月考）已知四边形ABCD，90ABCCAD，22ABBCAD，将ABC沿AC翻折至PAC△.（Ⅰ）若PAPD，求证：APCD；（Ⅱ）若二面角PACD的余弦值为14，求PD与面PAC所成角的正弦值.【答案】（Ⅰ）证明见解析

；（Ⅱ）10514.【解析】（Ⅰ）取CD的中点E，连接AE，PE不妨设2AD，则2ABBC，即2APPC因为90ABCCAD，所以2AC，则AECD，又因为PAPCPD，所以PECD，

且AEPEE，∴CD面PAE，PA面PAE，则APCD.（Ⅱ）取AC的中点O，连接PO，OE，PE，不妨设2AD，则2ABBC，即2APPC因为90ABCCAD，则POAC，又因为O为AC中点，E为CD的中点，则//OEAD，所以OEAC，所以POE

为二面角PACD的平面角.因此以点O为坐标原点，以OA，OE，Oz分别为x，y，z轴建空间直角坐标系如图：1,0,0A，1,2,0B，1,0,0C，1150,,44P设面PAC的法向量为,,nxyz，

2,0,0CA，1150,,44OP，9151,,44DP则20115044xyz，所以0x，令15y，则1z，所以面PAC的一个法向量为0

,15,1n，设PD与面PAC所成的角为，则105sin14||||nDPnDP.22．（2020·全国专题练习）如图，在长方体1111ABCDABCD中，1,2,,ABADEF分别为1,ADAA的中点，Q

是BC上一个动点，且(0)BQQC.（1）当1时，求证：平面BEFP平面1ADQ；（2）是否存在，使得BDFQ？若存在，请求出的值；若不存在，请说明理由.【答案】(1)证明见解析；(2)答案见解析.【解析】(1)当1时，Q为BC中点，因为E是AD的中点，所以,EDBQED

BQ∥,则四边形BEDQ是平行四边形，所以BEQD.又BE平面1,ADQDQ平面1ADQ，所以BE平面1ADQ.因为,EF分别是1,ADAA中点，所以1EFAD.因为EF平面11,ADQAD平面1ADQ，所以EF平面1ADQ.因为,BEEFEEF平面,BEFBE平面BEF，所

以平面BEFP平面1ADQ.(2)如图，连接,AQBD与FQ,因为1AA平面,ABCDBD平面ABCD，所以1AABD.若,BDFQ又1,AAFQ平面1AAQ，且1AAFQF，所以BD平面1AAQ.因为AQ平面1AA

Q，所以AQBD.在矩形ABCD中，由AQBD，得AQBDBA∽,所以2ABADBQ.又1,2ABAD，所以13,22BQQC,则13BQQC，即13.