【文档说明】2021年人教版高中数学选择性必修第二册（精讲)拓展一《利用递推公式求通项公式常用方法》（原卷版）.doc，共(6)页，812.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38101.html

以下为本文档部分文字说明：

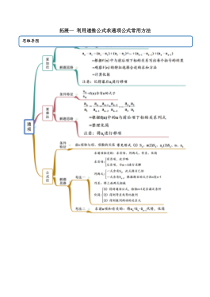
拓展一利用递推公式求通项公式常用方法思维导图考法一累加法【例1】（2020·湖北茅箭·十堰一中月考）数列na中，11a，12,nnnaannnN，则na___________.【

一隅三反】1．（2020·自贡市第十四中学校高一期中）已知数列na满足112a，121nnaann，则na__________.2．（2020·吉林朝阳·长春外国语学校高二开学考试）设数列na中，112,1nnaaan，则通项na_______

____．考法二累乘法【例2】．（2020·安徽省泗县第一中学开学考试）已知11a，1nnnanaanN，则数列na的通项公式是（）A．21nB．11nnnC．2nD

．n【一隅三反】常见考法1．（2020·黑龙江伊春二中高一期中）已知12a，12nnnaa，则数列na的通项公式na等于（）A．2122nnB．2122nnC．2222nnD．2222nn

2．（2020·横峰中学开学考试（理））在数列na中，11a，32122223nnaaaaannN，则na______．考法三公式法【例3】（1）（2020·湖北沙区·沙市中学期末）已知数列{an}的前n项和Sn＝n2+n，则an＝_____．（2）（2020·江西

省信丰中学月考）若数列的前n项和2133nnSa，则的通项公式是na________【一隅三反】1．（2020·上海市实验学校高一期末）数列na的前n项和23nnS，则其通项公式na________.2．（2020

·山西大同·一模（文））已知nS为数列na的前n项和，若111,23nnaaS，则数列na的通项公式为___________.3．（2020·尤溪县第五中学高一期末）.已知数列na满足2312

3222241nnnaaaa，则na的通项公式___________________．考法四倒数法【例4】（2020·南充西南大学实验学校高一月考）若数列na满足11nnnaaa，且123a，则10a___________.【一隅三反】1．（2020

·四川高一期末）设数列na的前n项和nS满足11nnnnSSSSnN，且11a，则na_____．3．（2020·四川成都）若数列na满足1121nnnaaa（2n，

*nN），且112a，则na（）A．12nB．2nC．1122nD．222n考法五构造法【例5】（2020·双峰县第一中学高二开学考试）数列na中，若11a，1231nnaan，则该数列的通项na（

）A．123nB．23nC．23nD．123n【一隅三反】1．（2020·贵州省思南中学月考）已知数列{}na中，112,21nnaaa则na___________.2．（2019·兴安县第三中学高二期

中）已知数列na满足11a132nnaa，则na的通项公式为__________________．