【文档说明】02021年高中数学人教版必修第一册：4.4《对数函数》精品讲义(含解析).doc，共(17)页，1.066 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31171.html

以下为本文档部分文字说明：

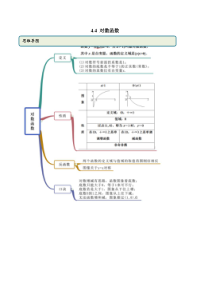
4.4对数函数思维导图常见考法考点一对数函数的概念辨析【例1-1】（2019·全国高一）下列函数表达式中，是对数函数的有（）①log2xy；②logayxaR；③8logyx；④lnyx；⑤log2xyx；⑥42logyx

；⑦2log1yx.A．1个B．2个C．3个D．4个【答案】B【解析】由于①中自变量出现在底数上，①不是对数函数；由于②中底数aR不能保证0a，且1a，②不是对数函数；由于⑤⑦的真数分别为2x，1x，⑤⑦也不是对数函数；

由于⑥中4logx的系数为2，⑥也不是对数函数；只有③④符合对数函数的定义.故选：B【例1-2】（2020·宝鸡市渭滨中学高一期中）若函数()lo1gafxx(0,1)aa的图像过点(7,3)，则a的值为（）A．2B．2C．22D

．12【答案】B【解析】由题,373log182aaa.故选：B【一隅三反】1．（2020·全国高一课时练习）下列函数为对数函数的是（）A．y＝logax＋1(a＞0且a≠1)B．y＝loga(2x)(a＞0且a≠1)C．y＝log(a－1)

x(a＞1且a≠2)D．y＝2logax(a＞0且a≠1)【答案】C【解析】根据对数函数的定义，可得判定，只有函数(1)log(1ayxa且2)a复数对数函数的概念，所以函数(1)log(1ayxa且2)a是对数函数，而选项A、B、D中

的函数只能是对数型函数，不是对数函数.故选：C.2．下列函数是对数函数的是()A．3log(1)yxB．ylog2ax(a0,a1)C．lnyxD．2ylogax(a0,a1)【答案】C【解析】由对数函数定义可以，本题选C．3．下列函数，是

对数函数的是A．y=lg10xB．y=log3x2判断一个函数是对数函数的方法C．y=lnxD．y=log13（x–1）【答案】C【解析】由对数函数的定义，形如y=logax（a>0，a≠1）的函数是对数函数，由此得到：y=lg10x=x，y=2

3logx=23logx、y=13log1x都不是对数函数，只有y=lnx是对数函数．故选C．4．（2020·全国高一课时练习）对数函数的图象过点M(16,4)，则此对数函数的解析式为()A．y＝log4xB．y＝14logxC．y＝12logx

D．y＝log2x【答案】D【解析】由于对数函数的图象过点M(16,4)，所以4＝loga16，得a＝2所以对数函数的解析式为y＝log2x，故选D.考点二单调性（区间）【例2】（1）（2020·辽宁锦州·高二期末）函数2223fxlogxx的单调减区间是（）A．3,1B．(

)1,+?C．1,1D．1,3（2）（2019·四川省新津中学高一月考）已知()log(32)afxax在1,2上是增函数，则实数a的取值范围是（）A．(0,1)B．30,2C．30,4D．33,42【答案

】（1）D（2）C【解析】由题：2230xx，130xx，解得：1,3x，23log23fxxx的减区间，即2yx2x3的减区间，对称轴为1x结合二次函数单调性，所以23log45fxxx的减区间1,3.故

选：D（2）设()32uxax，()log(32)afxax在[1,2]上是增函数，01(2)0au，即01340aa，解得304a，实数a的取值范围是30,4，故选：C．【一

隅三反】1．（2019·小店·山西大附中高一期中）函数213log(32)yxx的单调递减区间为（）A．2,B．3,2C．,1D．3,2【答案】A【解析】因为213log(32)yxx，所以2320xx，解得1x

或2x令232txx，因为232yxx的图像开口向上，对称轴方程为32x，所以内函数232txx在2,上单调递增，外函数13logyt单调递减，所以由复合函数单调性的性质可知函数213log(32)yxx的单调递减区间为2,故选A.2．函数y=1

2logx是A．区间（–∞，0）上的增函数B．区间（–∞，0）上的减函数C．区间（0，+∞）上的增函数D．区间（0，+∞）上的减函数【答案】A【解析】如图所示，函数y=12logx的图象与函数y=12logx的图象关于y轴对称，所以函数y=12logx是区间（–∞，0）

上的增函数．故选A．函数单调性的判断方法，一般地，增函数与增函数的和为增函数，增函数与减函数的差为增函数，复合函数的单调性的判断方法是同增异减，对于与对数函数有关的复合函数，注意真数恒大于零的要求.3．（2020·全国）已知

函数2()lg(45)fxxx在(,)a上单调递增，则a的取值范围是（）A．(2,)B．[2,)C．(5,)D．[5,)【答案】D【解析】由2450xx得5x或1x所以fx的定义域为,1(5,)因为245yxx在(5,)上单调

递增所以2()lg(45)fxxx在(5,)上单调递增所以5a故选：D考点三定义域和值域【例3】（1）（2020·永昌县第四中学高二期末（文））函数1()ln(-1)-2fxxx的定义域为（）A．1,2B．1,C．

2,D．1,22,（2）（2019·新疆兵团第二师华山中学高二月考（文））函数212log617yxx的值域是（）.A．RB．,3C．8,D．3,【答案】（1）C（2）B【解析】（1）要使得函数有意

义，只需：20x且10x，解得2,x.故函数定义域为2,.故选：C.（2）22617380xxx恒成立，函数212log617yxx的定义域为R设22617388txxx

由复合函数的单调性可知函数212log617yxx在定义域R上先增后减，函数取到最大值即：21122log617log83yxx函数的值域为,3故选B【一隅三反】1．（2020·沭阳县

修远中学高二期末）函数22log2fxxx的定义域为（）A．0,2B．0,2C．2,D．2,【答案】A【解析】函数22log2fxxx的定义域满足：200xx，解得02x.故选：A.2．（2020·湖南高新技术产业园区·衡阳市一中高三月

考）已知函数()fx的定义域是[1,1]，则函数(21)()ln(1)fxgxx的定义域是________.【答案】(0,1)【解析】由题意，函数()fx的定义域是[1,1]，即11x，

则函数(21)()ln(1)fxgxx有意义，则满足12111011xxx，解得0110xxx，解得01x，即函数(21)()ln(1)fxgxx的定义域是(0,1).故答案为：(0,1).3．（2019·北）若函数22,1,()log,

1,xxfxxx则函数()fx的值域是（）A．(,2)B．(,2]C．[0,)D．(,0)(0,2)具体函数的定义域的求解，求解原则如下：（1）分式中分母不为零；（2）偶次根式中被开方数非负；（3）对数中真数大于零，底数大于零且不为1；（4）正切函数tany

x中，2xkkZ；（5）求定义域只能在原函数解析式中求，不能对解析式变形.【答案】A【解析】画出函数的图像如下图所示，由图可知，函数的值域为,2，故选A.考点四比较大小【例4】（2020·全国高一课时

练习）比较下列各组数中两个值的大小．（1）log23.4，log28.5；（2）log0.31.8，log0.32.7；（3）loga5.1，loga5.9(a>0，且a≠1)．【答案】（1）22log3.4log8.5；（2）0.30.3log1.8log2

.7；（3）当01a时，log5.1log5.9aa；当1a时，log5.1log5.9aa.【解析】（1）根据对数函数2logfxx在(0,)为单调递增函数，因为3.48.5，所以22log3.4log8.5.

（2）根据对数函数0.3logfxx在(0,)为单调递减函数，因为1.82.7，所以0.30.3log1.8log2.7.（3）根据对数函数logafxx的性质，可得：当01a时，函数logafxx在(

0,)为单调递减函数，因为5.15.9，所以log5.1log5.9aa；当1a时，函数logafxx在(0,)为单调递增函数，因为5.15.9，所以log5.1log5.9aa.【一隅三反】1．（202

0·辽源市田家炳高级中学校高二期末（文））已知2log0.3a，1.30.3b，1.32c，则a，b，c的大小关系是（）A．abcB．cabC．bcaD．bac【答案】A【解析】22log

0.3log10a,1.3000.30.31b,1.322c,abc,故选：A2．（2020·哈尔滨市第十二中学校高二期末（文））已知0.2log2a，20.2b，0.23c，则（）A．abcB．acbC．cabD

．bca【答案】A【解析】0.2log20a，20.2(0,1)b，0.231c，所以abc，故选：A.3．（2020·贵州铜仁伟才学校高二期末（文））若30.6a，3log0.2b，0.63c，则（）A．cab

B．acbC．cbaD．bca【答案】A【解析】因为0.63331,log0.20,00.61，所以0101abc，，，故cab.故选：A.考点五解不等式【例5】（2020

·内蒙古集宁一中高二期末（文））不等式0.25log(1)1x的解集是________.【答案】51,4比较对数式的大小，主要依据对数函数的单调性．1．若底数为同一常数，则可由对数函数的单调性直接进行

比较．2．若底数为同一字母，则根据底数对对数函数单调性的影响，对底数进行分类讨论．3．若底数不同，真数相同，则可以先用换底公式化为同底后，再进行比较，也可以利用顺时针方向底数增大的规律画出函数的图象，再进行比较．4．若底数与真数都不同，则常借助1,0等中间量进行比较【解析】由0.25logf

xx在0,单调递减，因为0.250.25log11log0.25x，所以1010.25xx，解得，514x，即解集为51,4.故答案为:51,4【一隅三反】1．（

2020·安徽马鞍山）已知函数(2)fx是定义域为R的偶函数，()fx在(2,)上单调递减，则不等式(ln)(1)0fxf的解集是（）A．(0,1)(3,)B．（1，3）C．3(0,)(,)e

eD．3(,)ee【答案】C【解析】因为(2)fx的图象是由fx的图象向左平移2个单位，而2fx的图象关于y轴对称，故fx的图象关于直线2x对称.由()fx在(2,)上单调递减可得()fx在(,2)上单调递增，故(ln)(1)0fxf即为(ln)(1

)fxf，也就是ln2211x，所以ln1x或ln3x，解得0xe或3xe，故选：C．2．（2020·湖北）已知函数fx是定义在R上的奇函数，当,0x时，22fx

xx，若实数m满足2log3fm，则m的取值范围是（）A．0,2B．1[,2]2C．0,8D．1[,8]8【答案】A【解析】当0,x时，,0x，2222fxxxxx，因为fx是定义在R上的奇函

数，所以22fxfxxx，即22fxxx.因此，222,0,2,0.xxxfxxxx作出fx的图象如下：fx在R上单调递增，又13f，由2log31fmf得：2log1m，解得：02m.故选：A.3．（2

019·山东省实验中学高三月考）已知函数logagxx(a>0且a≠1)的图像过点(9，2)(1)求函数gx的解析式；(2)解不等式315gxgx．【答案】（1）3loggxx（2）3,52【解析】(1)因为log92a

，所以3a，即3loggxx(2)因为gx单调递增，所以3150,xx即不等式的解集是3,52考点六定点【例6】（2020·山东省枣庄市第十六中学高一期中）函数l

og3afxxx的图象恒过定点A，（其中0a且1a），则A的坐标为__________.【答案】4,4【解析】令31x，解得4x，所以44f，所以A的坐标为4,4，故答案为：4,4【一隅三反】1.（2020·云南省玉溪第一中学高一期中）

函数log(32)2ayx的图象必过定点（）A．(1,2)B．(2,2)C．(2,3)D．2,23【答案】A【解析】∵log(32)2ayx过定点，∴321,1xx，=log1+

22ay，故图象必过定点()1,2．故选：A．2．（2019·重庆高一月考）函数()log(1)1afxx（0a，且1a）的图象恒过点（）A．(1,1)B．(2,1)C．(1,2)D．(2,2)【答案】B【解析】真数为1时，对数为0，所以令x=2，则f（x）=1，所以函数fx的图

象过定点2,1.考点七图像【例7】（2020·哈尔滨市第十二中学校高二期末（文））函数log()ayx（0a且1a）与函数xya（0a且1a）在同一直角坐标系内的图象可能是（）A．B．C．D．【答案】A【解析】当01a时，xya和logayx均

为减函数，而log()ayx的图象和logayx的图象关于y轴对称，结合选项知A、B、C、D均错误；当1a时，xya和logayx均为增函数，而log()ayx的图象和logayx的图象关于y轴对称，结合选项可得A正确.故选：A【一隅三反】1．（2020·山东滨州·高二期末）函

数ln1fxx的图象大致是（）A．B．C．D．【答案】A【解析】ln1,101fxxxx，,所以舍B;当(1,)x时,ln(1)fxx单调递增，所以舍去CD，故选：A2．（2020·全国高一课时练习）函数y＝2log4(1－x)的图象大致是

A．B．C．函数y＝logax(a＞0且a≠1)的底数变化对图象位置的影响．观察图象，注意变化规律：(1)上下比较：在直线x＝1的右侧，a＞1时，a越大，图象向右越靠近x轴，0＜a＜1时a越小，图象向右越靠近x轴．(2)左右比较：比较图象与y＝1的

交点，交点的横坐标越大，对应的对数函数的底数越大．D．【答案】C【解析】函数42log(1)yx－的定义域为1xx且单调递减，故选C.3.如图，若C1，C2分别为函数y＝logax和y＝logbx的图象，则()A．0＜

a＜b＜1B．0＜b＜a＜1C．a＞b＞1D．b＞a＞1【答案】B【解析】作直线y＝1，则直线与C1，C2的交点的横坐标分别为a，b，易知0＜b＜a＜1.考点八对数函数综合运用【例8】（2020·甘肃省会宁县第四中学高二期末（文））已知函数22log3log3fxxx

．（1）求(1)f的值；（2）求函数()fx的定义域（3）判断函数()fx的奇偶性，并证明.【答案】(1)3；(2)3,3；(3)偶函数，证明见解析．【解析】(1)令1x，则221log4log2213f(2)由题意:3030xx

，解得33x，故定义域为3,3；(3)函数()fx为偶函数证明：对任意3,3x，22log3log3fxxxfx由偶函数的定义可得函数()fx为偶函数【一隅三反】1．（2020·湖南桃江·高二期末）已

知函数()log(1)(0xafxaa且1)a.（1）求()fx的定义域；（2）解关于x的不等式()(1)fxf.【答案】（1）当1a时，定义域为(0,)，当01a时，定义域为(,0)；（2）(0,1).【解析】（1）由函数有意义得1

xa，∴当1a时，定义域为(0,)，当01a时，定义域为(,0).（2）∵1x在定义域内，∴1a∴()fx单调递增，结合定义域可知：()(1)fxf的解集为(0,1).2．（2020·山东省枣庄市第十六

中学高一期中）已知函数121()log21axfxx，a常数.（1）若2a，求证()fx为奇函数，并指出()fx的单调区间；（2）若对于35,22x，不等式1221log(21)log(21)4xxmx恒成立，求

实数m的取值范围.【答案】（1）证明见解析，单调增区间为11(,),(,)22；（2）98m.【解析】（1）证明：当2a时，1221()log21xfxx.()fx的定义域为11,22

.当11,,22x时,11222121()()loglog2121xxfxfxxx11222121loglog102121xxxx.()()0f

xfx，∴()fx在区间11,,22上是奇函数，()fx的单调增区间为1,2，1,2.（2）由1221log(21)log(21)4xxmx，得21211log214xxmx

.令12211()log214xxgxx，若使题中不等式恒成立，只需要min()gxm.由（1）知()gx在35,22上是增函数，所以min39()28gxg

.所以m的取值范围是98m.