【文档说明】2021年人教版高中数学必修第二册(精讲)8.3《简单几何体的表面积与体积》（解析版）.doc，共(14)页，660.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38879.html

以下为本文档部分文字说明：

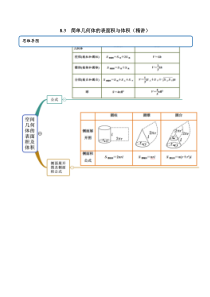
8.3简单几何体的表面积与体积（精讲）思维导图考法一多面体表面积【例1】（1）（2020·全国高一课时练习）已知正六棱柱的高为6，底面边长为4，则它的表面积为（）A．4833B．48323C．2462D．144（2）（2021·江苏南京市）已知

一个正三棱台的两个底面的边长分别为4和16，侧棱长为10，则该棱台的侧面积为（）.A．80B．240C．320D．640【答案】（1）A（2）B【解析】（1）由题知侧面积为664144，两底面积之和为23246483

4，所以表面积常见考法4833S.故选：A.（2）由题意可知，该棱台的侧面为上下底边长为4和16，腰长为10的等腰梯形等腰梯形的高为：221641082等腰梯形的面积为：

14168802S棱台的侧面积为：3380240SS本题正确选项：B【一隅三反】1．（2020·湖南怀化市）已知正四棱柱(即底面是正方形的直棱柱)的底面边长为3cm，侧面的对角线长是35cm，则这个正四棱柱的表面积为()A．290

cmB．2365cmC．272cmD．254cm【答案】A【解析】由题意侧棱长为22(35)36．所以表面积为：224362390()Scm．故选：A.2．（2020·张家界市民族中学高一月考）棱长为1的正四面体的表面积为（）A．3B．23C．33D．43【答案】

A【解析】如图由正四面体的概念可知，其四个面均是全等的等边三角形，由其棱长为1，所以13sin6024ABCSABAC，所以可知：正四面体的表面积为43ABCS，故选：A3．（2020·长春市第二实验中学高一期末）正三棱锥底面边长为a

，高为66a，则此正三棱锥的侧面积为（）A．234aB．232aC．2334aD．2332a【答案】A【解析】因为底面正三角形中高为32a，其重心到顶点距离为323233aa，且棱锥高66a，所以利用

直角三角形勾股定理可得侧棱长为22632632aaa骣骣鼢珑鼢+=珑鼢珑鼢鼢珑桫桫，斜高为2221222aaa骣骣÷ç÷ç÷-=ç÷ç÷ç÷ç÷÷桫ç桫，所以侧面积为21133224Saaa=创=.选A.考法二多面体台体积【例2】（2020·江苏南京市）底面边长为2，高为1的正三棱柱的体积

是（）A．3B．1C．32D．13【答案】A【解析】底面边长为2，高为1的正三棱柱的体积是23(2)134故选：A【一隅三反】1．（2020·河北秦皇岛市）如图，已知高为3的棱柱111ABCABC的底面是边长为1的正三角形，则三棱锥1BABC的体

积为（）A．14B．12C．34D．36【答案】C【解析】三棱锥1BABC的体积为：1113311333224ABCSh故选：C2．（2020·广东惠州市·高一期末）正四棱锥的底面边长和高都等于2，则该四棱锥的体积为（）A．233B．223C．83D．8【答案】C【解

析】∵正四棱锥的底面边长和高都等于2，∴该四棱锥的体积211822333VSh.故选：C.3．（2020·六盘山高级中学高一月考）已知棱长均为4，底面为正方形的四棱锥SABCD如图所示，求它的体积.【答案】3223【解析】

如图所示：连接AC，BD交于点O，连接SO，因为四棱锥的棱长均为4，所以SO平面ABCD，即SO为四棱锥的高，所以4,22SAOA,所以2222SOSAOA，所以113224422333VABADSO.4．（2020·北京高一

期末）如图，正三棱锥PABC的底面边长为2，侧棱长为3.（1）求正三棱锥PABC的表面积；（2）求正三棱锥PABC的体积.【答案】（1）623；（2）233.【解析】（1）取BC的中点D，连接PD，在RtPBD△中，可得2222PDPBBD.∴1222PBCSBC

PD△.∵正三棱锥的三个侧面是全等的等腰三角形，∴正三棱锥PABC的侧面积是362PBCS△.∵正三棱锥的底面是边长为2的正三角形，∴122sin6032ABCS△.则正三棱锥PABC的表面积为623；（2）连接AD，设O为正三角形ABC的中心

，则PO底面ABC.且1333ODAD.在RtPOD中，22693POPDOD.∴正三棱锥PABC的体积为12333ABCSPO△.考法三旋转体的表面积【例3】（2020·山东德州市·高

一期末）若圆锥的轴截面是顶角为120的等腰三角形，且圆锥的母线长为2，则该圆锥的侧面积为（）A．3B．2C．23D．43【答案】C【解析】如图圆锥的轴截面是顶角为120，即60APO，2AP，9

0POA,所以3AO，所以圆锥的侧面积为23AOPA.故选：C.【一隅三反】1．（2021·浙江高一期末）一个圆柱的侧面展开图是一个正方形，则这个圆柱的表面积与侧面积的比值是（）A．142B．122C．12D．142【答案】

B【解析】设圆柱的底面半径为r，圆柱的高为h，圆柱的侧面展开图是一个正方形，2rh，圆柱的侧面积为2224rhr，圆柱的两个底面积为22r，圆柱的表面积为22222224rrhrr

，圆柱的表面积与侧面积的比为：22222241242rrr，故选：B．2．（2020·全国高一）把一个半径为20的半圆卷成圆锥的侧面，则这个圆锥的高为（）A．10B．103C．102

D．53【答案】B【解析】半径为20的半圆卷成圆锥的侧面，则圆锥的底面圆周长为220r，所以底面圆的半径为r=10，所以圆锥的高为222010103h.故选：B3．（2020·全国高一课时练习）一个圆柱内接于一个底面半径为2，高为4的圆锥，则内接圆柱侧面积的最大值是（）A．32

B．3C．5D．4【答案】D【解析】圆锥的底面半径为2，高为4，设内接圆柱的底面半径为x，则它的上底面截圆锥得小圆锥的高为422xx，因此，内接圆柱的高42hx；圆柱的侧面积为224242Sxxxx

(02)x，令22121txxx，当1x时，1maxt；所以当1x时，4maxS，即圆柱的底面半径为1时，圆柱的侧面积最大，最大值为4.故选：D.考法四旋转体的体积【例4】（2021·宁夏银川市·贺兰县景博中学）已知圆锥的母线长为

5，底面周长为6，则它的体积为（）A．10B．12C．15D．36【答案】B【解析】设圆锥的底面半径为r，高为h，因为底面周长为6，所以26r，解得3r，又因为母线长为5，所以h=4，所以圆锥的体积是21123Vrh故选：B【一隅三反】1．（2020·浙江

杭州市·高一期末）将半径为3，圆心角为23的扇形作为侧面围成一个圆锥，则该圆锥的体积为（）A．B．22C．3D．223【答案】D【解析】由扇形弧长公式可求得弧长2323L，圆锥底面周长为2，圆锥底面半径1r，圆锥的高223122h，

圆锥的体积212233Vrh.故选：D.2．（2020·威海市教育教学研究中心高一期末）古代将圆台称为“圆亭”，《九章算术》中“今有圆亭，下周三丈，上周二丈，高一丈，问积几何？”即一圆台形建筑物，下底周长3丈，上底周长2丈，高1丈，则它的体积为（）A．198立方丈

B．19立方丈C．198立方丈D．19立方丈【答案】B【解析】由题意得，下底半径32R（丈），上底半径212r（丈），高1h（丈），所以它的体积为222211313113322VhRrRr

所以19V(立方丈).故选：B.3．（2020·贵州毕节市·高一期末）已知圆锥的表面积为9，它的侧面展开图是一个半圆，则此圆锥的体积为（）A．3B．3C．9D．9【答案】B【解析】

设圆锥的底面半径为r，高为h，则母线长为22lrh，则圆柱的侧面积为2221122rrh，故表面积为222192rhr，得2231922rh①，又底面圆周长等于侧面展开半圆的弧长，故222rrh，即222rrh

，得223hr②，联立①②得：3r，3h.故该圆锥的体积为21133333VSh.故选：B.考法五球【例5】（1）（2020·长春市第二实验中学高一期末）已知一个正方体的8个顶点都在同一个球面上

，则球的表面积与这个正方体的表面积之比为（）A．3B．2C．32D．312（2）．（2021·江西景德镇市·景德镇一中高一期末（理））已知一个正三棱锥的四个顶点都在一个球的球面上，且这个正三棱锥的所有棱长都为22，求这个球的

表面积（）A．4B．8C．12D．24【答案】（1）B（2）C【解析】（1）设正方体的棱长为a，球的半径为R，则3232RaRa，球的表面积为222134432SRaa，正方

体的表面积为226Sa，2122362SaSa.故选：B（2）设该正三棱锥为ABCD，将三棱锥ABCD补成正方体AEBFGCHD，如下图所示：则正方体AEBFGCHD的棱长为22222，该正方体的体对角线长为23，所以，正三棱锥

ABCD的外接球直径为223R，可得3R，该球的表面积为2412SR.故选：C.【一隅三反】1．（2020·浙江高一期末）若一个球的直径为2，则此球的表面积为（）A．2B．16C．8D．4【答案】D【

解析】因为球的直径为2，即球的半径为1，所以球的表面积为2414，故选：D.2．（2020·天津和平区·耀华中学高一期末）棱长为2的正方体的外接球的表面积为（）A．4B．43C．12D．43【答案】C【解析】因为正方体的外接球的直径为正方体的体对角线的长，

所以223R，解得3R，所以球的表面积为：2412SR.故选：C3．（2021·宁夏长庆高级中学高一期末）已知一个正方体的体积为8，求此正方体内切球的表面积为（）A．43B．8C．4D．16【答案】C【解析】正方体的体积为8，故边长为2，内切

球的半径为1，则表面积244SR，故选：C.4.（2020·山东济宁市·高一期末）将一个棱长为3cm的正方体铁块磨成一个球体零件，则可能制作的最大零件的体积为（）A．39cmB．39m2cC．392cmD．3273cm2【答案

】B【解析】正方体的棱长为3cm，所以球体最大体积的半径32rcm，所以球的体积：334932Vrcm.故选：B考法六组合体的体积表面积【例6】（2020·全国高一课时练习）如图，一个无盖的器皿是由棱长为3的正方体木料从顶部挖掉一个直径为2的半球而成（半球的底面圆在正方体

的上底面，球心为上底面的中心），则该器皿的表面积S为（）A．54B．542C．54D．543【答案】C【解析】器皿的表面积是棱长为3的正方体的表面积减去半径为1的圆的面积，再加上半径为1的半球

的表面积，即器皿的表面积221633141542542S．故选：C．【一隅三反】1．（2020·山东菏泽市·菏泽一中高一月考）某组合体如图所示，上半部分是正四棱锥PEFGH，下半部分是长方体ABCDEFGH.正四棱锥PEFGH的高为3，2E

F，1AE，则该组合体的表面积为（）A．20B．4312C．16D．438【答案】A【解析】由题意，正四棱锥PEFGH的斜高为312，该组合体的表面积为122421422202.故选

：A2．（2020·河北沧州市一中高一期末）鲁班锁（也称孔明锁、难人木、六子联方）起源于古代中国建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分（即榫卯结构）啮合，十分巧妙.鲁班锁类玩具比较多，形状和内部的构造各不相同，一般都是易拆难装.如图1，这是一种常见的鲁班锁玩具，

图2是该鲁班锁玩具的直观图，每条棱的长均为2，则该鲁班锁的表面积为（）A．8(6623)B．6(8823)C．8(6632)D．6(8832)【答案】A【解析】由题图可知，该鲁班锁玩具可以看成是一个棱长为222的正方体截去了8个正三棱锥所余下来的几何体

，且被截去的正三棱锥的底面边长为2，侧棱长为2，则该几何体的表面积为2116(222)42282322S8(6623).故选：A.3．（2021·周至县第二中学高一期末）如图所示，一个圆锥形的空

杯子上面放着一个半球形的冰淇淋，如果冰淇淋融化后正好盛满杯子，则杯子高h_______cm．【答案】8【解析】由题意得半球的半径和圆锥底面圆的半径4r，如果冰淇淋融化后正好盛满杯子，则半球的体积等于圆锥的体积所以32141448233hh故答案为：8