【文档说明】2021年人教版高中数学必修第二册(精讲)8.2《立体图形的直观图》（解析版）.doc，共(13)页，671.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38871.html

以下为本文档部分文字说明：

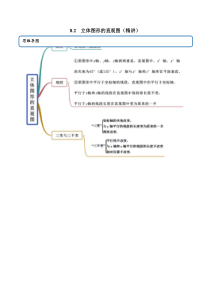
8.2立体图形的直观图（精讲）思维导图考法一平面图形的直观图【例1-1】按图示的建系方法，画水平放置的正五边形ABCDE的直观图．【答案】参考答案见试题解析．【解析】画法：（1）在图（1）中作AG⊥x轴于G，作DH⊥x轴于H．（2）在图（2）中画相

应的x′轴与y′轴，两轴相交于点O′，使∠x′O′y′＝45°．（3）在图（2）中的x′轴上取O′B′＝OB，O′G′＝OG，O′C′＝OC，O′H′＝OH，y′轴上取O′E′＝OE，分别过G′和H′作y′轴的平行线，并

在相应的平行线上取G′A′＝GA，H′D′＝HD．常见考法（4）连接A′B′，A′E′，E′D′，D′C′，并擦去辅助线G′A′，H′D′，x′轴与y′轴，便得到水平放置的正五边形ABCDE的直观图A′B′C′D′E′（如图（3））．【例1-2】．如图，四边形ABCD是边长为1的正方形

，且它是某个四边形按斜二测画法画出的直观图，请画出该四边形的原图形，并求出原图形的面积.【答案】图像见解析，22【解析】画出平面直角坐标系xOy，使点A与原点O重合，在x轴上取点C，使2AC，再在y轴上取点D，使2AD，取AC的中点E，连接DE并延长至点B，使DEEB，连接DC，CB，BA，

则四边形ABCD为正方形''''ABCD的原图形，如图所示.易知四边形ABCD为平行四边形.∵2AD，2AC，∴2222ABCDS，即原图形的面积为22.【一隅三反】1．一个菱形的边长为4cm，一内角为60°，将菱形

水平放置并且使较长的对角线成横向，试用斜二测画法画出这个菱形的直观图。【答案】见解析.【解析】菱形直观图如下：2．画出图中水平放置的四边形ABCD的直观图.【答案】图见解析.【解析】由斜二测画法：纵向减半，横向不变；即可知A、C在对应点1(3,1),(0,)2AC，而B

、D对应点,BD位置不变，如下图示：3．如图，ABCV是水平放置的ABC斜二测画法的直观图，6AC，4BC，能否判断ABC的形状并求AB边的实际长度是多少？【答案】答案见解析【解析】根据斜二测画法规则知：90ACB

，故ABC为直角三角形，ABC中，6AC，8BC，故2210ABACBC.考法二空间几何体的直观图【例2-1】用斜二测画法画一个棱长为3cm的正方体的直观图.【答案】见解析【解析】如图所示：在空间直角坐标系中画出一个正方体的直观图

，擦除坐标轴，即可得到直方图的直观图.【例2-2】．用斜二测画法画一个正六棱柱的直观图.【答案】见解析【解析】（1）如图，在正六边形ABCDEF中，取AD所在直线为x轴，AD的垂直平分线MN为y轴，两轴相交于点O.在图中，画相应的x轴与

y轴，两轴相交于点'O，使'45xOy；（2）根据斜二测画法法，画出正六边形ABCDEF水平放置的直观图ABCDEF；（3）画侧棱，过,,,,,ABCDEF各点分别作z轴的平行线，得到正六棱柱的侧棱；（4）成图，顺次连接,,,,,ABCDEF，

并加以整理（去掉辅助线，将被遮挡的部分改为虚线），【一隅三反】1．用斜二测画法画一个上底面边长为1cm，下底面边长为2cm，高（两底面之间的距离，即两底面中心连线的长度）为2cm的正四棱台.【答案】见解

析【解析】（1）画轴.如图（1）所示，画x轴、y轴、z轴，三轴相交于点O，使45,90xOyxOz.（2）画下底面.以点O为中点，在x轴上截取线段2cmMN，在y轴上截取线段1PQcm，分别过点,M

N作y轴的平行线，过点,PQ作x轴的平行线，设它们的交点分别为,,,ABCD，四边形ABCD就是正四棱台的下底面.（3）画高.在Oz上截取2cmOO，过O分别作平行于,OxOy的直线',OxyO.（4）画上底面.在平面'xOy上用画正四棱台下底面的方

法画出边长为1cm的正四棱台的上底面的直观图ABCD.（4）成图.顺次连接,,,AABBCCDD，整理（去掉辅助线，将被遮挡的部分改为虚线）得到正四棱台的直观图，如图（2）所示.2．用斜二测画法画出底面

边长为2cm，侧楼长为3cm的正三棱柱的直观图.【答案】见解析.【解析】正三棱柱直观图如图：3．画底面半径为1cm，母线长为3cm的圆柱的直观图。【答案】见解析.【解析】圆柱直观图如图：4．画出各条棱长都相等

的正六棱柱（底面是正六边形，侧棱垂直于底面）的直观图.【答案】见解析【解析】第一步：画x轴、y轴、z轴，使45xOy，90xOzo第二步：按x轴、y轴，画正六边形的直观图ABCDEF第三步：过,,,,,ABCDEF各点分别作z轴的平行线，并

在这些平行线上分别截取,,,,,AABBCCDDEEFF都等于棱AB的长第四步：顺次连接,,,,,ABCDEF，去掉辅助线及字母，将被遮挡的部分改为虚线，就得到所求作的正六棱柱的直观图.考法三直观图与

原图的周长面积【例3】如图是水平放置的四边形ABCD的斜二测直观图ABCD，且ADy轴，ABxP轴，则原四边形ABCD的面积是（）A．14B．102C．28D．142【答案】C【解析】（方法一）还原平面图形，如图左所示，延长DA

，交x轴于E，如图右所示，画出平面直角坐标系，取OEOE，过点E作EFy轴，在EF上截取2EAAE，28ADAD，再过点D作DCx∥轴，过点A作ABx轴，并截取2DCDC，5ABAB.连接BC，可得直观图AB

CD的原平面图形ABCD.由作出的图形可知，1(25)8282ABCDS四边形.（方法二）因为4AD，所以梯形ABCD的高为22，故122(25)722ABCDS

，则2228ABCDABCDSS四边形梯形.故选：C【一隅三反】1．ABC是边长为1的正三角形，那么ABC的斜二测平面直观图'''ABC的面积（）A．616B．68C．38D．34【答案】A【解析】以AB所在直线为x轴，线段AB的垂直平分线为

y轴，建立直角坐标系，画对应的'x轴，'y轴，使'''45xOy，如下图所示，结合图形，ABC的面积为113312224ABCSABOC，作CDAB'''，垂足为D，则22122224CDOCOCOC'''，''ABAB，所以'''A

BC的面积11222244ABCABCSABCDOCABS''''''，即原图和直观图面积之间的关系为2=4SS直观图原图，所以，'''ABC的面积为2364416ABCS'''.故选：A.2．用斜二测画法画如图所

示的直角三角形的水平放置图，正确的是（）A．B．C．D．【答案】B【解析】可以以直角顶点为坐标原点建立坐标系，由斜二测画法规则知，在直观图中此角为钝角，排除C和D，又原三角形的高在y轴上，在直观图中在y上，长度减半，排除A.故

选：B.3．ABC为边长为2cm的正三角形，则其水平放置《斜二测画法》的直观图的面积为______．其直观图的周长为______．【解析】如图所示ABC为边长为2cm的正三角形，则其水平放置的直观图'''ABC的面积为'''A

BCS12BCOA12sin45°＝12×2×（12×2×sin60°）×sin45°＝64；其直观图'''ABC的周长为LABBCCA＝2233121cos13522+2+22331

21cos4522＝（62+12）+2+（62﹣12）＝2+6.故答案为：64，2+6.考向四斜二测法【例4】关于“斜二测画法”,下列说法不正确的是()A．原图形中平行于x轴的线段,其对应线段

平行于x轴,长度不变B．原图形中平行于y轴的线段,其对应线段平行于y轴,长度变为原来的12C．在画与直角坐标系xOy对应的坐标系xOy时,xOy必须是45°D．在画直观图时,由于选轴的不同,所得的直观图可能不同【答案】C【解析】根据斜二测画

法的规则,平行于x轴或在x轴上的线段其长度在直观图中不变,平行于y轴或在y轴上的线段其长度在直观图中变为原来的12,并且45xOy或135°,故选：C.【一隅三反】1．利用斜二测画法画直观图时，下列说法中正确

的是（）①两条相交直线的直观图是平行直线；②两条垂直直线的直观图仍然是垂直直线；③正方形的直观图是平行四边形；④梯形的直观图是梯形.A．①②B．③④C．①③D．②④【答案】B【解析】根据斜二测画法的规则，可得两条相交直线的直观图仍然是相交直线，所以①错；两条垂直直线的直观图是两条

相交但不垂直的直线，所以②错；根据直观图的画法中，平行性保持不变，可得③，④正确.故选：B.2.下列说法正确的是（）A．互相垂直的两条直线的直观图仍然是互相垂直的两条直线B．梯形的直观图可能是平行四边形C．矩形的直观图可能是梯形D．正方形的直观图可

能是平行四边形【答案】D【解析】A项，原图形相互垂直的两条直线在直观图中不一定相互垂直,故A项错误。B项，原图形中平行的两条线段仍然平行，不平行的两条线段也不会平行，所以梯形的直观图不可能为平行四边形，故B项

错误。C项，原图形相互垂直的两条直线在直观图中不一定仍然相互垂直，但是原图形相互平行的两条线段在直观图中仍然互相平行，所以矩形的直观图中对边仍然平行，所以矩形的直观图可能为平行四边形而不能为梯形。故C项错误。D项，原图形相互垂直的两条直线在直观图中不一定仍然相互垂直，但是原图形相互平行的两

条线段在直观图中仍然互相平行，所以正方形中垂直的两边不一定仍然垂直，但是对边仍然平行，所以正方形的直观图可能是平行四边形。故D项正确。选D3.下列命题中正确的是()A．利用斜二测画法得到的正方形的直观图

是正方形B．利用斜二测画法得到的平行四边形的直观图是平行四边形C．有两个面平行，其余各面都是平行四边形的几何体叫棱柱D．用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台【答案】B【解析】利用斜二测画法得到的正方形的直观图是平行四边形；利

用斜二测画法得到的平行四边形的直观图是平行四边形；有两个面平行，其余各面都是平行四边形的几何体不一定是棱柱；用一个平行于底面的平面去截棱锥，底面与截面之间的部分组成的几何体才是棱台；因此B正确，选B.