【文档说明】2021年人教版高中数学必修第二册(精讲)7.3《复数的三角表示》（解析版）.doc，共(12)页，726.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38859.html

以下为本文档部分文字说明：

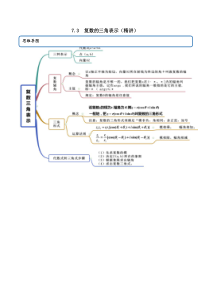
7.3复数的三角表示（精讲）思维导图考法一复数的三角表示【例1-1】（2020·全国高一课时练习）把下列复数的代数形式化成三角形式.（1）33i；常见考法（2）22i.【答案】（1）111133i23cosisin66（2）77cosisin22i244

【解析】（1）223323r.因为与33i对应的点在第四象限，所以11arg33i6，所以111133i23cosisin66.（2）22222r.因为与22i对应的点在第四象限，所以7arg22i4，所以7

7cosisin22i244.【例1-2】．（2020·全国高一课时练习）把下列复数的三角形式化成代数形式.（1）4cosisin33；（2）553cosisin4

4.【答案】（1）223i（2）3232i22【解析】（1）4cosisin4cos4sini33331344i223i22.（2）55552232323cosisin3co

s3sini33ii44442222.【一隅三反】1．（2020·全国高一课时练习）画出下列复数对应的向量，并把这些复数表示成三角形式：（1）1322i

；（2）1i.【答案】（1）作图见解析;13cossin2233ii（2）作图见解析;7712cossin44ii【解析】（1）复数1322i对应的向量如图所示，则221311,cos222r

.因为与1322i对应的点在第一象限，所以13arg223i.于是13cossin2233ii.（2）复数1i对应的向量如图所示，则22121(1)2,cos22r.因为与1i对应的点在第四象限，所以7

arg(1)4i.于是7712cossin44ii.当然，把一个复数表示成三角形式时，辐角不一定取主值.例如2cossin44i也是1i的三角形式.2．（2020·全国高一课时练习）将下列各复数的三角形式转化为代数形

式：（1）43(cossin)i；（2）11116cossin66i；（3）4432cossin33i；（4）338cossin22i.【答案

】（1）43（2）333i（3）323622i（4）8i【解析】（1）43(cossin)43(10)43ii.（2）1111316cossin63336622iii

.（3）4413323632cossin32332222iii.（4）338cossin8(0)822iii.3．（2020·全国高一课时练习）将下列各复数转化为三角形式（辐角取辐角主值）：（1）232i；（2）-

2i；（3）13i；（4）3.【答案】（1）11114cossin66i；（2）332cossin22i；（3）552cossin33i；（4）3(cossin)i【解析】

（1）∵22(23)(2)4r，3cos2，1sin2，又[0,2)，∴116，∴11112324cossin66ii.（2）∵2r=，cos0，sin1，又[0,2

)，∴32，∴3322cossin22ii.（3）∵221(3)2r，1cos2，3sin2，又[0,2)，∴53，∴55132cossin33ii.（4）∵3r，cos1

，sin0，又[0,2)，∴.∴33(cossin)i.考法二复数的辅角【例2】（2020·全国高一课时练习）复数55sincos1818zi的辐角主值为（）A．518B．169

C．29D．79【答案】D【解析】5577sincoscossin181899zii,故复数z的辐角主值为79.故选：D【一隅三反】1.（2020·全国）复数11z，2z由向量1OZ绕原点O逆时针方向旋转3而得到.则21arg()2zz的值为（）A．6B．3C．

23D．43【答案】C【解析】11z,1cos0sin0zi,1213(cossin)3322iZiOOZ21113()2222zzi所以复数在第二象限，设幅角为，tan323故选：C2．

（2020·全国高一课时练习）若复数13zi（i为虚数单位），则argz为（）A．120B．120°C．240°D．210°【答案】C【解析】由13zi，得复数z对应的点在第三象限，且1cos2，所以arg240z.故选：C.3．（2020·辽宁辽师

大附中高一期末）把复数z1与z2对应的向量OAOB，分别按逆时针方向旋转4和53后，重合于向量OM且模相等，已知213zi，则复数1z的代数式和它的辐角主值分别是（）A．22i，34B．322,4iC．22,4iD．22,4i

【答案】B【解析】由题可知1255cossincossin4433zizi，则122131322222ziii，1221222221112222izi

iiii，可知1z对应的坐标为2,2，则它的辐角主值为34.故选：B.考法三复数的乘、除运算的三角表示及及其几何意义【例3】（2020·全国高一课时练习）计算下列各式：（1）223cossin23cossin3333ii

；（2）112cos15sin1522i；（3）552cossin2cos135sin13533ii；（4）132coss

in2233ii.【答案】（1）6；（2）6222i；（3）313122i；（4）2644i【解析】（1）223cossin23cossin3333ii

226cosisin6(cossin)63333i.（2）112cos15sin1522ii2332cossincossi

n1212244ii332cosisin12412455312cossin26622ii6222i.（3）552cossin2cos135sin

13533ii55332cossin2cossin3344ii25353cossin34342i

11112cossin1212i2cossin1212i6262244i313122i.（4）132cossin2233ii

55cossin2cossin3333ii155cosisin33332244cossin233i213222i2644i

.【一隅三反】1．（2020·全国高一课时练习）cosisin3cosisin2266（）A．333i22B．333i22C．333i22D．333i22【答案】C【

解析】cosisin3cosisin3cosisin22662626223333cosisini3322.故选：C2．（2020·全国高一课时练习）9cos3isi

n33cos2isin2（）A．3B．3C．3iD．3i【答案】B【解析】9cos3isin33cos2isin2933.故选：B3．（2020·全国高一课时练习）1cos30sin302cos60sin603cos4

5sin452iii（）A．323222iB．323222iC．323222iD．323222i【答案】C【解析】1cos30sin302cos60sin602

ii3cos45sin45i123cos306045sin3060452i3cos135sin135i22322i323222i.故选：C.4．（2020·全国高一课时练习）计算下列

各式，并作出几何解释：（1）222cossin22cossin3333ii（2）112cos75sin7522ii（3）334cos300sin3002cossin44ii

（4）132cossin2233ii.【答案】（1）-4，几何解释见解析（2）6222i，几何解释见解析（3）(31)(31)i，几何解释见解析（4）1344i，几何解释见解析【解析】（

1）原式222(cossin)4(10)4i.几何解释：设12222cossin,22cossin3333zizi，作与12,zz对应的向量12,OZO

Z，然后把向量1OZ绕原点O按逆时针方向旋转3，再将其长度伸长为原来的22倍，得到一个长度为4,辐角为π的向量OZ，则OZ即为积124zz所对应的向量.（2）原式2222cos75sin75222ii

22cos75sin75cos315sin315231622cos390sin39022222iii.几何解释：设121122cos75sin75,co

s315sin315222zizi，作与12,zz对应的向量12,OZOZ，然后把向量1OZ绕原点O按逆时针方向旋转315°，再将其长度缩短为原来的22，得到一个长度为2、辐角为6的向量OZ，则OZ即为积126222zzi所对应的向量.（3）原式55334coss

in2cossin3344ii111122cossin22cossin12121212ii626222(31)(31)44ii.几何解释：设1

554cos300sin3004cossin33zii，2332cossin44zi作与12,zz对应的向量12,OZOZ，然后把向量1OZ绕原点0按顺

时针方向旋转34，再将其长度缩短为原来的12，得到一个长度为22，辐角为1112的向量OZ，则OZ即为12(31)(31)ziz所对应的向量.（4）原式22cossin2cossin3333ii

111313cossin23322244iii.几何解释：设11322cossin,2cossin223333ziizi，作与12,zz对应的向量12,OZOZ，然后把向量1OZ绕原点

0按顺时针方向旋转3，再将其长度缩短为原来的12，得到一个长度为12，辐角为3的向量OZ，则OZ即为121344ziz所对应的向量.