【文档说明】2021年人教版高中数学必修第二册(精讲)7.1《复数的概念》（解析版）.doc，共(7)页，592.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38847.html

以下为本文档部分文字说明：

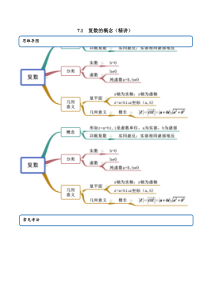
7.1复数的概念（精讲）思维导图常见考法考法一实部虚部的辨析【例1】（1）（2021·湖南永州市·高二期末）已知i是虚数单位，复数12zi的虚部为（）A．2B．2C．2iD．1（2）．（2020·河北秦皇岛市·秦皇岛一中高二月考）已知,xyR，且32xiyi，则,xy的值分别为（

）A．21,3B．3,1C．2,13D．1,3（3）（2020·江苏宿迁市·高二期中）3的平方根是________.【答案】（1）A（2）C（3）3i【解析】（1）复数12zi的虚部为2.故选：A.（2）由题意知，321xy，解得2

31xy，故选:C.（3）由233i得解.【一隅三反】1．（2020·上海静安区·高二期末）1的平方根为______．【答案】i【解析】21i，因此，1的平方根为i

.故答案为i.2．（2020·北海市教育教学研究室）复数322i（i是虚数单位）的实部为（）A．2B．32C．322D．0【答案】A【解析】根据复数的基本概念，可得复数322i的实部为2．故选：A．3．（2020·青海西宁市）若复数1(1)2zi，则z的共轭复

数的虚部是（）A．12iB．12iC．12D．12【答案】D【解析】因为复数111(1)222zii，所以z的共轭复数1122zi，虚部是12，故选：D．4．（2020·湖北十堰市·车城高中高二月考（理））以25i的虚部为

实部，以52i的实部为虚部的复数是（）A．2iB．22iC．55iD．45i【答案】B【解析】2552ii的虚部为2，5225ii的实部为2，则复数为22zi故选：B.考法二复数的分类【例2】（2020·吉林高

二期末（文））已知复数2262153mmzmmim（i是虚数单位）（1）复数z是实数，求实数m的值；（2）复数z是虚数，求实数m的取值范围；（3）复数z是纯虚数，求实数m的值.【答案】（1）5m；（2）5m且3m；（3）3m

或2.【解析】（1）复数z是实数，则2215030mmm，解得5m；（2）复数z是虚数，则221503mmm，解得5m且3m；（3）复数是纯虚数，则226032150mm

mmm，解得3m或2．【一隅三反】1．（2020·江苏宿迁市·高二期中）已知复数223183,zmmmmimR，其中i为虚数单位.（1）若复数z是实数，求实数m的值；（2）若复数z是纯虚数，求实数m的值.【答案】（1）

0或3；（2）6.【解析】（1）若复数z是实数，则230mm所以0m或3m.（2）若复数z是纯虚数，则22303180mmmm所以6m.2．（2020·江苏徐州市·高二期末）复数2152615zimimi．（1

）实数m取什么数时，z是实数；（2）实数m取什么数时，z是纯虚数；（3）实数m取什么数时，z对应的点在直线70xy上．【答案】（1）5m或3；（2）2m；（3）12m或2【解析】复数222(1)(52)(615)

(56)(215)zimimimmmmi．（1）由22150mm，解得5m或3．5m或3时，复数z为实数．（2）由225602150mmmm，解得2m．2m时，复数z为纯虚数．（3）由22(56)(215)70

mmmm．化为：22320mm，解得12m或2．12m或2，z对应点在直线70xy上．考法三复数的几何意义--复平面【例3】（1）（2020·四川成都市）已知复数34zi(i虚单

位)，则复数z在复平面内对应的点在（）A．第一象限B．第二象限C．第三象限D．第四象限（2）（2020·北京交通大学附属中学高二期末）在复平面内，若复数2246zmmmmi所对应的点在第二

象限，则实数m的取值范围是（）A．0,3B．,2C．2,0D．3,4【答案】（1）B（2）D【解析】（1）由复数的几何意义知，复数34zi在复平面内对应的点为3,4，即在第二象限，故选：B（2）∵在复平面内，

若复数2246zmmmmi所对应的点在第二象限，∴224060mmmm解得34x∴实数m的取值范围是3,4故选：D.【一隅三反】1．（2020·北京101中学

高二期中）在复平面内，复数1i的共轭复数所对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】D【解析】复数1i的共轭复数为1i，其对应的点1,1位于第四象限.故选：D.2．（2020·北京高二期末）设复数2zi，则z的共轭复数z

在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】D【解析】复数2zi的共轭复数2zi，则对应点的坐标为2,1，该点位于第四象限，故选：D.3．（2020·吉林

松原市·扶余市第一中学高二期中（文））若11zmmi（i是虚数单位）在复平面内对应的点位于第四象限，则实数m的取值范围为（）A．,1B．,1C．1,1D．1,【答案】C【解析】11zmmi对应的点为1,1mm，因为对应

的点位于第四象限，得1010mm，解得11m.故选：C.考法四复数的几何意义--模长【例4】（1）（2021·湖南郴州市·高二期末）设i虚数单位，复数12zi，则||z（）A．5B．5C．1D．2（2）

（2020·全国高二）已知(26)12ixyi，其中x､y是实数，则||xyi（）A．12B．32C．102D．2（3）（2020·广东佛山市·高二期末）设复数z满足2zi，z在复平面内对应的点为,xy，则（）A．22

14xyB．2212xyC．2214xyD．2214xy【答案】（1）A（2）C（3）D【解析】（1）2||125z故选：A（2）因为2612xxiyi，所以21x，62xy，解得12x，332yx，所以221310()()222xyi

，故选：C.（3）z在复平面内对应的点为,xy，则复数=,zxyixyR,则=12zixyi，由复数的模长公式可得22+1=4xy，故选：D【一隅三反】1．（2020·湖北随州市·高二月考）已知

i为虚数单位，实数x，y满足3xiiyi，则xyi（）A．10B．10C．3D．1【答案】B【解析】由(3)xiiyi，得3xiyi，1x，3y．则22||(1)(3)10

xyi．故选：B．2．（2021·宁夏银川市）复数12zi(其中i为虚数单位)，则3zi（）A．5B．2C．2D．26【答案】B【解析】因为12zi，所以31231ziiii所以223112zi.故

选：B.3．（2020·河北秦皇岛市·秦皇岛一中高二月考）已知复数z满足|2|1zi，则||z的最小值为（）A．51B．51C．31D．31【答案】A【解析】设zabi，则22221211ab

iiabiab，由22211xy，表示为以2,1为圆心，1为半径的圆，圆心到原点的距离为221=5，所以圆上点到原点距离最小为51，因为2222=00zabab，所以最小值为5

1，故选:A.4．（2021·徐汇区·上海中学高二期末）已知复数z满足条件1z，那么22zi的最大值为______．【答案】4【解析】因为1z，所以复数z对应的点在单位圆上，22zi表示复数z对应的点与复数22i对应的

点221M，之间的距离，而813OM．所以22zi的最大值为14OMrOM.故答案为：4