【文档说明】2021年人教版高中数学必修第二册(精讲)6.4.2《正余弦定理》（解析版）.doc，共(12)页，1.037 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38834.html

以下为本文档部分文字说明：

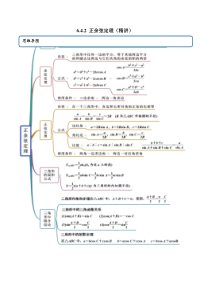
6.4.2正余弦定理（精讲）思维导图常见考法考法一余弦定理【例1】（1）（2020·全国高一课时练习）已知在ABC中，1a，2b，60C，则c等于（）A．3B．2C．5D．5（2）（2020·江西南昌市）在锐角ABC中，若5sin3A，2b

，3c，则a（）A．3B．22C．23D．5（3）（2020·全国高一课时练习）已知钝角三角形的三边长分别为,2,4kkk，则k的取值范围是（）A．(-2,6)B．(0,2)C．(0,6)D．(2,6)【答案】（1）A（2）D（3）D【解析】（1）在ABC中,1a,2b,60

C,由余弦定理得22212212cos603c,所以3c.故选:A（2）因为ABC为锐角三角形,5sin3A由同角三角函数关系式可得252cos133A又因为2b,3c由

余弦定理可得2222cosabcbcA代入可得224922353a所以5a故选:D（3）由题：钝角三角形的三边长分别为24kkk、、，2222424kkkkkk

解得：2,6k.故选：D【一隅三反】1．（2020·全国高一）在△ABC中，内角A，B，C的对边分别为a，b，c，右a=1，c=2，∠B=600，则b=（）A．1B．2C．3D．2【答案】C【解析】因为1a，2c

，60B，则由余弦定理可得222212cos1221232bacacB．故选：C．2．（2020·全国高一课时练习）在ABC中,内角A,B,C所对的边分别为a,b,c,且::3:5:7abc,则此三角形中的最大角的大小为（）A．150B．120C．90D．135

【答案】B【解析】ABC中::3:5:7abc设3,5,70akbkckk,由余弦定理可得2222222925491cos2302abckkkCabk.因为C为三角形的内角,所

以此三角形中的最大角120C,故选:B.3．（2020·北京人大附中高一期末）在ABC中，6ABC，3AB，3BC，则AC等于（）A．3B．3C．21D．21【答案】A【解析】因为6ABC，3AB，

3BC，所以22232cos9323332ACBCABBCABABC，即3AC，故选：A.考法二正弦定理【例2】（1）（2020·辽宁锦州市·高一期末）在ABC中，内角A，B，C的对边分别为a，b，

c，2a，23c，30A，则角C为（）A．60°B．60°或120°C．45°D．45°或135°（2）（2020·湖北黄冈市·高一期末）在△ABC中，内角A，B，C的对边分别为a，b，c，已知3cos5A，8a，5b，则B（）

A．4B．6C．3D．56（3）（2020·全国高一课时练习）已知△ABC的内角A，B，C的对边分别为a，b，c，若A＝60°，a3，则sinsinbcBC等于（）A．12B．3C．32D．2【

答案】（1）B（2）B（3）D【解析】（1）由正弦定理得sinsinacAC得2231sin2C得3sin2C，ca，CA，得60C或120，故选：B．（2）因为3cos5A，所以A为钝角

，4sin5A，B为锐角．由sinsinabAB得45sin15sin82bABa，所以6B．故选：B．（3）A＝60°，a3，由正弦定理可得，3sinsinsin32bcaBCA2，∴b＝2sinB，

c＝2sinC，则sinsinbcBC2．故选：D．【一隅三反】1．（2020·和县第二中学）在ABC中，45,2,3Aab，则B（）A．60B．60或120C．45D．135【答案】B【解析】由正弦定理可得sinsinabAB，23sin32sin22bABa

，0,πB，π3B或2π3.故选：B.2．（2020·吉林长春市实验中学）在ABC中，若2a，23b，30A，则B等于（）A．30°B．30°或150C．60D．60或120【答案】D【解析】由题意，在ABC中，由正弦定理可得sinsinabAB，即233sinsi

nsin3022bBAa，又由ab，且0180B，所以60B或120B，故选：D.3．（2020·合肥市第十一中学高一期末）已知△ABC中，,,164ABa，则b等于（）A．2B

．1C．3D．2【答案】D【解析】由正弦定理sinsinabAB，得1sinsin42sinsin6aBbA.故选：D．4．（2020·眉山市彭山区第一中学高一期中）在ABC中，角A、B、C所对的边分别是a、b、c，若1c，45B

，3cos5A，则b等于（）A．35B．107C．57D．5214【答案】C【解析】3cos5AQ，(0,180)A．24sin15AcosA，32422coscos()(coscossinsin)()525210CABAB

AB．272sin110CcosC．由正弦定理可得：sinsinbcBC，21sin52sin77210cBbC．故选：C．5．（2020·湖南岳阳市）在ABC中，若sincosABab，则角B的值为（）

.A．30°B．45°C．60°D．90°【答案】B【解析】因为sincosABab，所以sincosbAaB由正弦定理可得sinsinsincosBAAB，又sin0A，所以sincosBB，即tan10180BB

。。，，所以45B故选：B考法三正余弦定理综合运用【例3-1】（射影定理）（2020·安徽和县）在△ABC中，角A，B，C的对边分别为a，b，c，若a＝3，则bcosC+ccosB＝（）A．1B．2C．3D．4【答案

】C【解析】由余弦定理得bcosC+ccosB＝2222abcbab+2222acbcac＝222aa＝a＝3，故选：C.【例3-2】（2020·深圳市）在ABC中，角A，B，C的对边分别为a，b，c，

若sinsinsinsinBAcBCab，则A（）A．6B．3C．23D．3或23【答案】B【解析】因为sinsinsinsinBAcBCab，由正弦定理得bacbcab，整理得

222bcabc，由余弦定理得2221cos222bcabcAbcbc，又因为0,A，所以3A，故选：B【例3-3】（判断三角形形状）（2020·江苏省）在ABC中，60B，2

bac，则ABC一定是A．锐角三角形B．钝角三角形C．等腰三角形D．等边三角形【答案】D【解析】ABC中，60B，2bac,2222221cos20022acbBacacacac故得到ac，故得到角A等于角C，三角形为等边三角形.故答案为D.【例3-4】（三角

形个数判断）（2020·进贤县第一中学）若满足条件60,3,CABBCa的三角形ABC有两个，那么a的取值范围是（）A．1,2B．2,3C．3,2D．1,2【答案】C【解析】根据正弦定理可知sinsinABBCCA，代入可求得sin2aA因为60C，所以

60,120A若满足有两个三角形ABC则3122a所以3,2a所以选C【一隅三反】1．（2020·新疆巴音郭楞蒙古自治州·高一期末）在锐角ABC中，角A、B所对的边长分别为a、b，若2sin3aBb，则A等于（）A．60B．120C．30°D．150

【答案】A【解析】因为2sin3aBb所以由正弦定理可得2sinsin3sinABB，因为sin0B，所以3sin2A因为角A为锐角，所以60A故选：A2．（2020·四川成都市·双流中学高一开学考试）在ABC中，若cosbcA，则ABC

是（）A．直角三角形B．等腰三角形C．等边三角形D．等腰直角三角形【答案】A【解析】将cosbcA，利用正弦定理化简得：sinsincosBCA，把sinsin()sincoscossinBACAC+AC代入得：sincoscossinsinco

sACACCA，整理得：sincos0AC，即sin0A或cos0C，A，C为三角形内角，sin0A，cos0C，即2C，则ABC为直角三角形，故选：A.3．（2020·安徽宿州市·高一期末

）设ABC的三个内角A，B，C所对的边分别为a，b，c，如果3abcacbac，且23b，那么ABC外接圆的半径为（）A．2B．4C．23D．8【答案】A【解析】∵3abcacbac

，∴223acbac，化为：222acbac.∴2221cos222acbacBacac，∵0,B，∴3B，判断三角形解的个数的两种方法①代数法：根据大边对大角的性质、三角形内角和公式、正弦函数的值域等判断．②几何图形法：根据条件画出

图形，通过图形直观判断解的个数．∵23b，由正弦定理可得2324sin32bRB，解得2R，即ABC外接圆的半径为2.故选：A.4．（2020·浙江湖州市）在ABC中，边a，b，c所对的角分别为A，B，C，

若2223abcbc，sin2cosCB，则()A．3AB．4BC．3cbD．2ca【答案】D【解析】2223abcbc，由余弦定理可得：22233cos222bcabcAbcbc，可得6A，1sin2A，sin2cosCB

，可得：5sin2cos6BB，可得：13cossin2cos22BBB，tan3B，由0,B，可得：3B，2C，2ca．故选D．5．（多选）（2020·广东高一期末）在ABC中，内角A、B、C所对的边分别为a、b、c，不解三角形，确定下列判

断错误的是（）A．B＝60°，c＝4，b＝5，有两解B．B＝60°，c＝4，b＝3.9，有一解C．B＝60°，c＝4，b＝3，有一解D．B＝60°，c＝4，b＝2，无解【答案】ABC【解析】对于A，因为B为锐角且45cb，所以三角形ABC有唯一解，故

A错误；对于B，因为B为锐角且3sin4233.92cBbc，所以三角形ABC有两解，故B错误；对于C，因为B为锐角且3sin42332cBb，所以三角形ABC无解，故C错误；对于D，因为B为锐角且3sin42322cBb

，所以三角形ABC无解，故D正确.故选：ABC.6．（2020·四川省武胜烈面中学校高一期中）若满足2c，cossinaCcA的ABC有两个，则边长BC的取值范围为A．1,2B．1,3C

．3,2D．2,2【答案】D【解析】因为cossinaCcA，所以sincossinsintan14ACCACC,因此sin2sinsincBCAAC32(,)(,)sin(,1)(2,2)42242AABC，选D.考法四三角形的面积

公式【例4】（1）（2020·全国高一）在△ABC中，其外接圆半径R＝2，A＝30°，B＝120°，则△ABC的面积_____.（2）（2020·重庆高一开学考试）在ABC中，1cos4B，2b，sin2sinCA，则ABC的面积等于（3）

（2020·广东深圳市·宝安第一外国语学校高一期中）在△ABC中，a，b，c分别是角A，B，C所对的边．若A＝3，b＝1，△ABC的面积为32，则a的值为【答案】（1）3（2）154（3）3【解析】（1）根据正弦定理可知24sinsinabRAB，所

以4sin302a，4sin12023b,18030CAB，所以ABC是等腰三角形，且2ac，1sin32ABCSacB.故答案为：3（2）由sin2sinCA及正弦定理得2ca．

在ABC中，由余弦定理得2222cosbacacB，所以22222124444aaaa，解得1a，所以2c．又21514sinBcosB，所以111515sin122244ABCSacB．（3）因为A

＝3，b＝1，32ABCS，所以1133sin12222ABCSbcAc，所以2c，由余弦定理得2222cos1422cos33abcbcA，所以3a【一隅三反】1．（2020·湖南长沙市·高一期末）在ABC中，,,abc分

别为,,ABC的对边，60,1Ab，这个三角形的面积为3，则a（）A．2B．10C．23D．13【答案】D【解析】依题意11sin1sin60322SbcAc，解得4c，由余弦定理得2214214cos6013a.

故选：D.2．（2020·全国高一课时练习）在△ABC中，角A，B，C所对的边分别为a，b，c，若2bcosCccosBacosB，且a=4，b=6，则△ABC的面积为________.【答案】6223【解析】∵coscos2cosbCBaB，由余弦定理可得2222

222222222abcacbacbbcaabacac，化简得222122acbac，即1cos2B，∵0B，∴3B.又∵a=4，b=6，代入2222cosbacacB

，得24200cc，解得226c或226c（舍去），∴113sin4(226)6223222SacB.故答案为:62233．（2020·宜宾市叙州区第二中学校高一月考）在ABC中，已知3A，1b，ABC的

外接圆半径为1，则ABCS（）A．33B．34C．32D．6【答案】C【解析】已知A=3，得sinA=32，∵b=1，R=1，根据正弦定理=2sinsinabRAB，得3a，sinB=12,∵ab，易知B为锐角，∴B=6,∴C=2根据三角形的面积

公式，S△ABC=13sin22abC.故选C.4．（2020·全国高一专题练习）在ABC中，60A，1b，其面积为3，则sinsinsinabcABC等于（）A．33B．2633C．23

93D．292【答案】C【解析】由题意知，1sin2SbcA，即13sin602c，解得c4，由余弦定理得22212cos1168132abcbcA，即13a，由于13239si

nsinsinsin332abcaABCA，故答案为C.