【文档说明】2021年人教版高中数学选择性必修第二册（精讲)4.4《数学归纳法》（原卷版）.doc，共(8)页，381.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38115.html

以下为本文档部分文字说明：

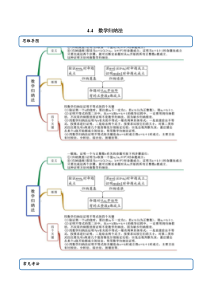
4.4数学归纳法思维导图常见考法考点一增项问题【例1】（2020·浙江海曙·效实中学）用数学归纳法证明123213521nnnnnnnnN的过程中，当n从k到1k时，等式左边应增乘的式子是（）A．21kB．

2122kkC．21221kkkD．221kk【一隅三反】1．（2020·上海市市西中学月考）1111112312nfnnn(*nN)，那么1fkfk共有（）项.A．21kB．2kC．21kD．以上都不对2．（2020·

江西期末（理））用数学归纳法证明不等式111131214nnnn的过程中，由nk递推到1nk时，不等式左边（）A．增加了121kB．增加了112122kkC．增加了11211kkD．增加了11121221kk

k3．（2020·甘肃省会宁县第二中学）用数学归纳法证明等式2135(21)nn（n∈N*）的过程中，第二步假设n=k时等式成立，则当n=k+1时应得到（）A．2135(21)kkB．2135(

21)(1)kkC．2135(21)(2)kkD．2135(21)(3)kk4．（2020·浙江绍兴·高一期末）用数学归纳法证明“11111(12322nnnnn

*)N”，由nk到1nk时，不等式左边应添加的项是（）A．121kB．122kC．112122kkD．11121221kkk考点二等式的证明【例2】．（2020·镇原中学）用数学归纳

法证明2222*121123N6nnnnn.【一隅三反】1．（2020·福建高二期中（理））用数学归纳法证明等式112222211234112nnnnn.2．（2020·广西钦州·高二期末（理））用数

学归纳法证明：2*1427311nnnnnNL.．考点三不等式的证明【例3】．（2019·浙江省春晖中学高二月考）用数学归纳法证明：1111ln12321nnnnnN.【一隅三反】1．（2

020·安徽高二期中（文））证明：不等式*11111123422nnnN，恒成立.2．（2020·安徽蚌山·蚌埠二中（理））试用数学归纳法证明2221111123(1)22nn

.考点四整除问题【例4】（2020·上海高二课时练习）用数学归纳法证明：2211112nn能被133整除*nN．【一隅三反】1．（2020·上海高二课时练习）求证：121*(1)nnaanN能被21aa

整除．2．（2020·上海高二课时练习）用数学归纳法证明：对任意正整数,4151nnn能被9整除．考点五数归在数列的应用【例5】．（2020·江西高二期末（理））设数列na的前n项和为nS，且对任意的正整数n都满足21nnnSaS．（1）求1S，2S，

3S的值，猜想nS的表达式；（2）用数学归纳法证明（1）中猜想的nS的表达式的正确性．【一隅三反】1．（2019·浙江余姚中学高二期中）已知数列na的前n项和为nS，214a，且1*1122nnnaSnnN

.（1）求12S、24S、38S；（2）由（1）猜想数列2nnS的通项公式，并用数学归纳法证明．2．（2020·浙江高三开学考试）已知等比数列na的公比1q，且23414aaa，31a是2

a，4a的等差中项，数列nb满足：数列nnab的前n项和为2nn．（1）求数列na、nb的通项公式；（2）数列nc满足：13c，*1,nnnnbccnNc，证明*12(2),2nnncccnN

3．（2020·四川省珙县中学月考）若n1n21(1,2,3,)aan，且11a.（1）求2a，3a，4a，5a，（2）归纳猜想通项公式na，用数学归纳法证明.