【文档说明】2021年人教版高中数学选择性必修第三册6.3《二项式定理》同步精讲（解析版）.doc，共(13)页，981.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-37476.html

以下为本文档部分文字说明：

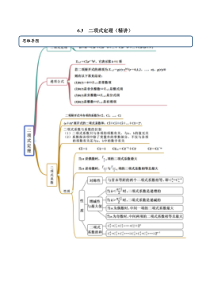
6.3二项式定理（精讲）思维导图常见考法考法一二项式定理展开式【例1】(1)求41(3x)x的展开式为．（2）（2020·江苏省太湖高级中学高二期中）已知012233444(1)4729nnnnnnnnCCCCC，

则n的值为【答案】（1）1x2＋12x＋54＋108x＋81x2【解析】（1）方法一3x＋1x4＝(3x)4＋C14(3x)3·1x＋C24(3x)21x2＋C34(3x)1x3

＋C441x4＝81x2＋108x＋54＋12x＋1x2.方法二3x＋1x4＝3x＋1x4＝1x2(1＋3x)4＝1x2·[1＋C14·3x＋C24(3x)2＋C34(3x)3＋C44(3x)4]＝1x2(1＋12x＋54x2＋1

08x3＋81x4)＝1x2＋12x＋54＋108x＋81x2.（2）由012233444(1)4729nnnnnnnnCCCCC得01203123123014141

41414729nnnnnnnnnnnCCCCC则12479n，即672933n，解得6n.【一隅三反】1．（2021·全国课时练习）化简多项式(2x+1)5-5(2x+1)4+10(2x+1)3-1

0(2x+1)2+5(2x+1)-1的结果是()A．(2x+2)5B．2x5C．(2x-1)5D．32x5【答案】D【解析】依题意可知，多项式的每一项都可看作55211rrrCx，故为5211x的展开式，化简555211232xx

x.故选D.2．（2020·江苏宿迁市·宿迁中学高二期中）化简：2012222412333...3nnnnnnnnCCCC_________.【答案】101n【解析】011020201211212(31)3131...3131nnn

nnnnnnnnCCCC则2012222412233331(31)10nnnnnnnnnnCCCC所以2012222412333...3101nnnnnnnnnCCCC故答案为：101n.考法二

二项式指定项的系数与二项式系数【例2】（1）（2020·全国高二单元测试）在(x-3)10的展开式中，x6的系数是（2）（2020·广东佛山市·高二期末）二项式81xx的展开式中常数项是_____

_（用数字作答）（3）（2020·安徽省蚌埠第三中学高二月考）3031xx的有理项共有项【答案】（1）9410C（2）70（3）6【解析】（1）由Tk+1=10kCx10-k(-3)k，令10-k=6，解得k=4，∴系数为(-3)4410

C=9410C（2）二项式81xx的展开式的通项公式8821881rrrrrrTCxCxx，令820r，得4r,则常数项为4588765==704321TC，故答案为：70（3）3031xx的通项公式为：5301036130301rr

rrrrTCxCxx，061051730300,,6,rTxrTxCC，1218051319303012,,18,rTxrTxCC，243010152531303024,,30,rTxrTxCC，所以有理项共

有6项，故选：C【一隅三反】1．（2020·北京市鲁迅中学高二月考）二项式261(2)xx的展开式中的常数项是_______.（用数字作答）【答案】60【解析】有题意可得，二项式展开式的通项为：626123166

12(1)2rrrrrrrrTCxCxx令1230r可得4r，此时2456260TC.2.（2021·上海青浦区）在6212xx二项展开式中，常数项是_______.【答案】60【解析】展开式的通项公式是626123166122rrrrr

rrTCxCxx，当1230r时，4r24416260TC.故答案为603.．（2020·青海西宁市）若83axx的展开式中4x的系数为7，则实数

a=______.【答案】12【解析】根据二项展开式的通项公式可得：48883318883=rrrrrrrrrrraTCxCaxCaxx，令4843r，可得3r，3388==7rrCaCa，解得：12a，故答案

为：124．（2020·梁河县）已知31(2)nxx的展开式的常数项是第7项，则n________.【答案】8【解析】根据题意，可知第7项为666366324122nnnnnCxCxx

，而常数项是第7项，则3240n，故8n.故答案为：8.考法三多项式系数或二项式系数【例3】（1）（2020·福建三明市·高二期末）52212xx的展开式中常数项是（）A．-252B．-220C．220D．252（2）．（2021·四川

成都市）若5(2)axxx的展开式中常数项为80，则a（）A．2B．1C．2D．1【答案】（1）A（2）C【解析】(1）由2510211(2)()xxxx，可得二项式101()xx的展开式通项为10102110101

()(1)rrrrrrrTCxCxx，令1020r，解得=5r，所以展开式的常数项为5510(1)252C.故选：A.（2）5axx的展开式的通项公式为：55251(1)rrrrrTCax，显然，

25r-为奇数，若求5(2)axxx展开式的常数项，251r，解得2r=故5(2)axxx的展开式的常数项等于：23580Ca2a故选：C.【一隅三反】1．（

2020·全国高三专题练习）4211xx展开式中常数项为（）.A．11B．11C．8D．7【答案】B【解析】将21xx看成一个整体，展开得到：41421()(1)rrrrTCxx421()rxx的展开式为：424

3144mrmmmrmmrrTCxxCx取430rm当0m时，4r系数为：40440(1)1CC当1m时，1r系数为：11143(1)12CC常数

项为11211故答案选B2．（2020·全国高三专题练习）524131xxxx的展开式中常数项为()A．30B．30C．25D．25【答案】C【解析】511x的通项为151(1)rrrrTCx，5522411311xx

xxxx55141311xxxx，根据式子可知当4r或2r=时有常数项，令4r414551(1)TCx;令2323512(1)rTCx

;故所求常数项为13553CC53025，故选C.3．（2020·河南商丘市）64111xx的展开式的常数项为（）A．6B．10C．15D．16【答案】D【解析】由题意得611x

的展开式的通项为160,1,2,,6rrrTCxr，令4r，则4615C，所以64111xx的展开式的常数项为11516.故选：D.4．（2

020·枣庄市第三中学高二月考）在1020201(1)xx的展开式中，x2项的系数为（）A．30B．45C．60D．90【答案】B【解析】在1020201(1)xx的展开式中，通项公式为Tr+110rC

•20201rxx.对于20201rxx，通项公式为Tk+1krC•xr﹣2021k，k≤r，r、k∈N，r≤10.令r﹣2021k＝2，可得r＝2+2021k，故k＝0，r＝2，故x2项的系数为210C•02C4

5，故选：B.5．（2020·全国高二专题练习）若1021xaxx的展开式中6x的系数为30，则a等于（）A．13B．12C．1D．2【答案】D【解析】将题中所给式子可化为10101022111xaxxxaxxxx

根据二项式定理展开式通项为1CrnrrrnTab,101xx的通项为10102110101rrrrrrTCxCxx令1024r解得3r所以6x的项为234610120xCxx令10

26r解得2r=所以6x的项为2661045aCxax综上可知,6x的系数为1204530a解得2a故选:D考法四二项式定理的性质【例2】（1）（多选）（2020·全国高二单元测试）111xx的展开式中二项式系数最大的项是（）A．第5项B．第6项C．第7项D．

第8项（2）（2020·山东省桓台第一中学高二期中）（多选）二项式1121xx的展开式中，系数最大的项为（）.A．第五项B．第六项C．第七项D．第八项（3）（2020·绵阳市·四川省绵阳江油中学高二开学考试）若1nxx

的展开式中只有第7项的二项式系数最大，则展开式中含2x项的系数是A．462B．462C．792D．792【答案】（1）BC（2）BC（3）D【解析】(1）因为n＝11为奇数，所以展开式中第1112项和第11112项，即第6项

和第7项的二项式系数相等，且最大.故选：BC（2）二项式1121xx的展开式中，每项的系数与二项式系数相等，共有12项所以系数最大的项为第六项和第七项故选：BC（3）∵1nxx的展开式中只有第7项的二项式系数最大，∴n为偶

数，展开式共有13项，则12n.121xx的展开式的通项公式为1212211CrrrrTx，令1222r，得5r.∴展开式中含2x项的系数是12551C792，故选D．【一隅三反】1．（2020·辽宁沈阳

市·高二期中）在1nxnN的二项展开式中，若只有第5项的二项式系数最大，则12nxx的二项展开式中的常数项为（）A．960B．1120C．-560D．-960【答案】B【解析】在（x﹣1）n（n∈N+）的二项展开式中，若只有第

5项的二项式系数最大，则n=8，则1(2)nxx=812xx的二项展开式的通项公式为Tr+1=8rC•28﹣r•（﹣1）r•x4﹣r，令4﹣r=0，求得r=4，可得展开式中的常数项为48C•24•（﹣1）4=1120，故

选B．2．（2021·湖南常德市）的展开式中各项系数的和为2,则该展开式中常数项为（）A．B．C．10D．20【答案】C【解析】由已知，当时，即，所以展开式中常数项为，故选.3．（多选）（2020·三亚华侨学校高二开学考试）已知nab的展开式

中第5项的二项式系数最大，则n的值可以为（）A．7B．8C．9D．10【答案】ABC【解析】∵已知nab的展开式中第5项的二项式系数4nC最大,则7n或n＝8或n＝9故选：ABC.4．（2020·全国高二课时练习）已知6(31)x展开式中各项系数的和为m

，且2lognm，求2nxx展开式中二项式系数最大的项的系数.【答案】59136【解析】设6260126(31)xaaxaxax，令1x，得6612(31)42m，所以2log

12nm，则122xx展开式中有13项，且中间一项（第7项）的二项式系数最大，该项为6666633712122()(2)59136TCxCxxx.故所求的系数为59136

.5．（2020·重庆市第七中学校高二月考）二项式*122nxnNx的展开式中，二项式系数最大的项是第4项，则其展开式中的常数项是_________．【答案】-20【解析】由题意知，展

开式中有7项，6n．因为661122rrrTrCxx6262612rrrrCx令620r，得3r，所以常数项为336120C．考法五二项式系数或系数和【例5】（2020·安徽省泗县）若2701277()(12)fxxaaxaxax

.求：（1）017aaa；（2）1357aaaa；（3）0127aaaa.【答案】（1）27；（2）14；（3）27.【解析】（1）令1x，可得301235674()3271faaaaaaaa

，∴4012356727aaaaaaaa．①（2）令1x可得301235674(1)(1)faaaaaaaa，∴401235671aaaaaaaa

．②由①②得13572()28aaaa，∴135714aaaa．（3）由题意得二项式7(12)x展开式的通项为177(2)2rrrrrrTCxCx，∴每项的系数0(0,1,2,,7)iai，∴01235017647227aaaaa

aaaaaaa．【一隅三反】1．（2020·北京朝阳区·高二期末）在5(21)x的二项展开式中，二项式系数之和为___________；所有项的系数之和为_______.【答案】32243【解析】根据二项展开式的

性质，展开式的二项式系数之和为52232n，令1x可得所有项的系数之和为55(211)3243，故答案为：32，2432．（2020·全国高二单元测试）若(2－x)10＝a0＋a1x＋a2x2＋…＋a10x10，则(a0＋a2＋…＋a10)2－(a1＋a3＋…＋a9

)2＝【答案】1【解析】令1x，得10011021aaa，令1x，得1001231021aaaaa，220210139aaaaaa0110012310aaaa

aaaa101021211.故选：A.3．（2020·福建厦门市·厦门双十中学高二期中）已知1121011012101112xaaxaxaxax，则12101121011aaaa_____.

【答案】22【解析】对等式112012(12)xaaxax10111011axax两边求导，得101222(12)2xaax91010111011axax，令1x，则1210112101122aa

aa.4．（2020·宁县第二中学高二期中）设2012(21)nnnxaaxaxax展开式中只有第1010项的二项式系数最大．（1）求n；（2）求012naaaa;（3）求.312

232222nnaaaa.【答案】（1）2018；（2）20183；（3）-1.【解析】（1）由二项式系数的对称性，1101020182nn（2）201801220180122018=3aaaaaaaa（3）令0x，得20180(1

0)1a，令12x，得21232018232018(11)02222aaaa，故3201812023201812222aaaaa.考法六二项式定理运用【例6】（1）（2020·上海市七宝中学高二期中）7271除以100的余数是________（2

）（2020·全国高二单元测试）6(1.05)的计算结果精确到0.01的近似值是_________【答案】（1）41（2）1.34【解析】（1）727217172727270727127270170177070CCC

C21072701()mmN2105041m即7271除以100的余数为41．故答案为：41．（2）66122661.0510.051+0.05+0.05+1+0.3+0.0375=

1.33751.34CC故答案为：1.34【一隅三反】1．（2020·四川棠湖中学高二月考）已知202074a能够被15整除，则a________.【答案】14【解析】由题可知，020202027571401201920200202012019201

91202002020202020202020751751751751CCCC0202012019201912020202020207575751CCC所以0202012019201912

020202022020200775754751CCCaa，而75能被15整除，要使202074a能够被15整除，只需1a能被15整除即可，所以115a，解得：14a.故答案为：14.2．（2020·江苏泰州市·泰州中学高二期中）83被5除所得的余数是________

_____．【答案】1【解析】因为883(52)0817262778088888855(2)5(2)5(2)5(2)CCCCCK071625277808888885(55(2)5(2)(2))5(2

)CCCCCK，所以转化为求80885(2)256C被5除所得的余数，因为2565151，所以83被5除所得的余数是1，故答案为：13．（2021·河北保定市）60.99的计算结果精确到0.001的近

似值是【答案】0.941【解析】6620126666330.9910.0110.010.010.01...CCCC10.060.00150.00002...0.941故选B