【文档说明】2021年高中数学人教版必修第一册：5.4《三角函数的图象与性质》精品讲义(含解析).doc，共(17)页，1.181 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31262.html

以下为本文档部分文字说明：

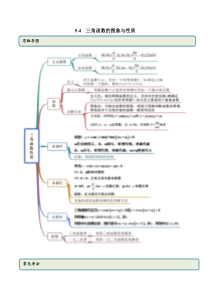
5.4三角函数的图象与性质思维导图常见考法考点一五点画图【例1】（1）（2020·全国高一课时练习）用五点法作出函数1cos(02)yxx的简图.（2）（2020·全国高一课时练习）利用正弦或余弦函数图象作出3sin2yx的图象．【答案】见解析【解

析】（1）列表:x02322cosyx101011cosyx01210描点，连线，如图.（2）由3sincoscos2yxxx，所以3sin2yx的图象由cosyx的图象x轴下方的部分关于x轴对称上去，和

x轴上方的原图象共同组成，如图实线部分所表示的是3sin2yx的图象【一隅三反】1．（2020·全国高一课时练习）利用“五点法”作出函数y＝1－sinx(0≤x≤2π)的简图．【答案】见解析【解析】列表：x02322sinx01010五点法画图作形如y＝asi

nx＋b(或y＝acosx＋b)，x∈[0,2π]的图象时，可用“五点法”作图，其步骤是：①列表，取x＝0、π2、π、3π2、2π；②描点；③用光滑曲线连成图．1sinx10121作图：2．（2020·全国高一课时练习）利用正弦

曲线，求满足13sin22x的x的集合．【答案】25(2,2][2,2)6336kkkk【解析】正弦函数一个周期内的图象如图，满足13sin22x，由图可知，25(2,2][2,2)6336xkkkk所以满足13s

in22x的x的集合为25(2,2][2,2)6336kkkk3．（2020·武功县普集高级中学高一月考）用五点法作出函数32cosyx在0,2内的图像.【答案】见解

析【解析】列表：x02322cosyx10－10132cosyx53135描点得32cosyx在0,2内的图像（如图所示）：考点二周期【例2】（1）（2020·福建高二学业考试）函数cosyx的最小正周期为（）A

．2B．C．32D．2（2）（2020年广东潮州）下列函数中，不是周期函数的是()A.y＝|cosx|B．y＝cos|x|C．y＝|sinx|D．y＝sin|x|【答案】（1）D（2）D【解析】（1）

函数cosyx的最小正周期为：2故选：D（2）画出y＝sin|x|的图象，易知y＝sin|x|不是周期函数【一隅三反】1．（2020·全国高一课时练习）下列函数中,最小正周期为的是()A．sinyxB．cosyxC．sin

2yxD．1cos2yx【答案】C【解析】对于:sinAyx，周期221T，错误.对于:cosByx，周期221T，错误.对于:sin2Cyx，周期22T，正确.对于D，1cos2yx

，周期2412T，错误，故选C.2．（2019·云南高二期末）函数()2sin36fxx的最小正周期为__________．【答案】23【解析】由题得函数的最小正周期22|-3|3T.故答案为：23考点三对称性【例3】（2020·辽宁大连·高一期末）函数c

os26fxx的图像的一条对称轴方程为（）A．6xB．512xC．23xD．23x【答案】B【解析】函数cos26fxx令26xkkZ，则,212kxkZ，当1k时，512x，故选B.【一隅三反】1．（2

020·永昌县第四中学高一期末）函数y＝12sin3x的图象的一条对称轴是（）A．x＝－2B．x＝2C．x＝－6D．x＝6【答案】C【解析】令()32xkkZ，则56xk

，kZ当1k时，6x，所以C成立，经检验，其他选项都不正确.故选：C2．（2020·山西省长治市第二中学校高一期末（理））下列函数中，最小正周期为，且图象关于直线3x对称的函数是（）A．2sin23yxB．2sin26yxC

．2sin23xyD．2sin23yx【答案】B【解析】先选项C中函数2sin23xy的周期为2412T,故排除C,将3x,代入A,B,D求得函数值为0,2,3

,而函数sin()yAxB在对称轴处取最值.故选:B.3．（2020·河南平顶山·高一期末）如果函数sin2yx的图象关于直线πx对称，那么取最小值时的值为（）A．3πB．π3C．π2D．

2π【答案】D【解析】由函数sin2yx的图象关于直线πx对称，可得22k，kZ，即32k，kZ，取最小值时1k，即2或2k，即2.故取最小值时的值为2π.故选：D.考点

四单调性【例4】（1）（2020·吉林扶余市第一中学高一期中）函数1πsin223fxx的单调递增区间为（）A．5πππ,π1212kk，kZB．π3ππ,π44kk

，kZC．2πππ,π36kk，kZD．πππ,π44kk，kZ（2）（2020·吉林扶余市第一中学高一期中）已知函数sin2fxx在π0,6上单调递减，则实数的一个值是（）．A．3π2B．π2

C．πD．2π【答案】（1）A（2）C【解析】（1）当πππ2π22π232kxk，kZ时，函数1πsin223fxx单调递增，即当5ππππ1212kxk，kZ时，函数

1πsin223fxx单调递增.故选：A（2）因为π0,6x，则3π2,x，又函数sin2fxx在π0,6上单调递减，所以π3,2,2322kk，kZ，因此

22π3232kk，kZ，解得：322,22kkkZ，故选：C．【一隅三反】1．（2020·湖南益阳·高一期末）函数cos26fxx的单调递增区间为（）A．7,1212kkk

ZB．72,266kkkZC．5,1212kkkZD．52,266kkkZ【答案】A【解析】由2226kxk

剟，kZ，得71212kxk剟，kZ，即函数的单调递增区间为7,1212kkkZ，故选：A．2．（2020·全国高三其他（理））已知函数sin06fxx，对任意xR，都有3fxf，并且fx

在区间,63上不单调，则的最小值是（）A．1B．3C．5D．7【答案】D【解析】由题意，3f是函数fx的最大值，2362k，即61,kkZ．0，kN．当0k时，1，sin6fxx在,

63上单调递增，不符合题意；当1k时，7，sin76fxx符合题意.的最小值为7.故选：D．3．（2020·全国高三其他（理））函数cosfxx

在0,上为增函数，则的值可以是（）A．0B．2C．D．32【答案】C【解析】对A,cosfxx,由余弦函数的性质可知fx在0,上为减函数，舍去；对B，cos2=-sinfxxx，在0,上先减后

增，舍去对C,coscosfxxx，由余弦函数的性质可知fx在0,上为增函数.成立；对D,=sin3cos2fxxx,在0,上先增后减，舍去故选：C．考点五奇偶性【例5】（202

0·上海黄浦·高一期末）下列函数中，周期是的偶函数为（）.A．cos2xyB．sin2yxC．|sin|yxD．sin||yx【答案】C【解析】A选项，函数cos2xyfx的定义域为R，且coscos22xxfxfx

，所以函数cos2xy为偶函数，周期为2412；B选项，函数sin2yfxx的定义域为R，且sin2sin2fxxxfx，所以函数sin2yx为奇函数，周期为22；C选项，函数|sin|yfxx的定义与为R，且

sinsinfxxxfx，所以函数|sin|yx为偶函数，周期为；D选项，函数sin||yfxx的定义域为R，且sinsinfxxxfx，所以函数sin||yx为偶函数，不具有周期性.故选：C【一隅三反】1．（2019·贵州高三月考（

文））函数sin2yx是（）A．最小正周期为2的奇函数B．最小正周期为的奇函数C．最小正周期为2的偶函数D．最小正周期为的偶函数【答案】B【解析】由题意，函数sin2fxx，则sin(2)sin2()fxxxfx，所以函数sin2fxx为奇函数

，且最小正周期22T，故选B.2．（2020·辽宁辽阳·高一期末）下列函数中，周期为的奇函数是（）A．cos2xyB．sin(23)yxC．cos(2)yxD．cos2yx【答案】B【解析】根据题意，依次分析选项：对于A，cos=-

sin22xxy，是奇函数，周期T＝2=412，不符合题意；对于B，y＝sin（2x+3π）＝﹣sin2x，是奇函数，周期T＝2=2，符合题意；对于C，cos(2)yx＝-cos2x，是

偶函数，不符合题意；对于D，cos=2yx|sinx|，是偶函数，不符合题意；故选：B．3．（2020·昆明市官渡区第一中学高一开学考试）已知函数3()sin42fxxxR，下面结论错误的是（）A．函数()fx的最

小正周期为2B．函数()fx在区间0,16上是增函数C．函数()fx的图象关于直线4x对称D．函数()fx是偶函数【答案】B【解析】对于函数3()sin4cos42fxxx，它的周期等

于242，故A正确．令4x，则()cos14f，则4x是()fx的对称轴，故C正确．由于()cos(4)cos4()fxxxfx，故函数()fx是偶函数，故D正确．利用排除法可得B错误；故选：B．考点六定义域【例6】（1）（2020·宁县第二中学

高一期中）函数1sinyx的定义域是________.（2）（2020·宁县第二中学高一期中）函数2116sinyxx的定义域是__________.【答案】（1）2,2kkkZ（2）[4,)(0,)【解析】（1）因为1sinyx，所以sin0

x，解得22,kxkkZ，即函数的定义域为2,2kkkZ故答案为：2,2kkkZ（2）因为2116sinyxx所以2160sin0xx，解2160x得44x，解sin0x得22,kxkkZ

，所以4xπ或0πx，故函数的定义域为[4,)(0,)故答案为：[4,)(0,)【一隅三反】1（2020·辽宁沈阳·高一期中）函数1tan24yx的定义域是（）A．4,2xxkkZ

∣B．2,2xxkkZ∣C．32,2xxkkZ∣D．,2xxkkZ∣【答案】B【解析】令1,242xkkZ，则2,2xkkZ，故选：B.2．（2020·湖南高一月考）函数3()=ln(sin-)2fxx

的定义域为（）A．2(,)()33kkkZB．5(,)()66kkkZC．2(2,2)()33kkkZD．5(2,2)()66kkkZ【答案】C【解析】由已知可得3sin2x，由正弦函数

的性质知222()33kxkkZ.故选：C.3．（2020·吉林公主岭·高一期末（理））函数3ln(sincos)()3xxxfxx的定义域为（）考查函数的定义域，即求使函数有意义的取值范围．求函数定义域的依据(1)整式函数的定义域为R

；(2)分式的分母不为零；(3)偶次根式的被开方数不小于零；(4)对数函数的真数必须大于零；(5)正切函数y＝tanx的定义域为π{|π,}2xxkkZ；(6)x0中x≠0；(7)实际问题中除要考虑函数解析式有意义外，还应考虑实际问题本身的要

求．A．0,3B．,43C．(,]43D．5,44【答案】C【解析】由sincos03030xxxx…得522,4433kxkkx

Z„所以(,]43x.故选：C.考点七值域【例7】（1）（2019·福建高三学业考试）函数2sinyx的最小值是。（2）（2020·全国高二月考（文））2cos38yx

在区间,88上的最小值为______.（3）（2020·全国高一课时练习）函数tanyx344x，且2x的值域是________________．【答案】（1）2（2）0（3

）,11,【解析】（1）当sin1x时，函数2sinyx的最小值是2，（2）因为,88x，所以3,842x，则cos30,18x，2cos30,28yx，故2co

s38yx在区间,88的最小值为0，故答案为：0.（3）函数tanyx在,42，值域为1,，在3,24也单调递增，值域为

,1，综上函数tanyx344x，且2x的值域是,11,.故答案为：,11,【一隅三反】1．（2019·伊美区第二中学高一月考）求函数24sin4cos2yxx的最值，及取

最值时x的集合．【答案】22,3xkkZ时，min3y；2,xkkZ时，max6y．【解析】由已知224(1cos)4cos24cos4cos2yxxxx214cos32x，∵1cos1x，∴当1cos2x，即22,3xk

kZ时，min3y，当cos1x，即2,xkkZ时，max6y．2．（2020·新疆高三三模（理））f(x)＝2sinωx(0<ω<1)，在区间0,3上的最大值是2，则ω＝_______

_.【答案】34【解析】函数f(x)的周期T＝2，因此f(x)＝2sinωx在0,上是增函数，∵0<ω<1，∴0,3是0,的子集，∴f(x)在0,3

上是增函数，∴3f＝2，即2sin3＝2，∴3ω＝4，∴ω＝34，故答案为34.3．（2020·山西省长治市第二中学校高一期末（理））已知函数()3sinfxx在区间[,

]34上的最小值为3，则ω的取值范围是（）A．9][6,)2(-,-B．93][,)22(-,-C．2][6,)(-,-D．32][,)2(-,-【答案】D【解析】因为,34x，

函数()3sinfxx在区间[,]34上的最小值为3，所以0时，,34x，所以32，32，0时，,43x，所以42，2，所以的范围是32][,)2(-,

-．故选：D．考点八正切函数性质【例8】（2020·山西省长治市第二中学校高一期末（理））下列关于函数πtan3yx的说法正确的是（）A．函数的图象关于点π,03成中心对称B．函数的定义域为π{|π,Z}6xxkkC．函数在区间5π,66π

上单调递增D．函数在区间5ππ[,]66上单调递增【答案】B【解析】tan333，A错；由32xk得,6xkkZ，B正确；5,66x时，7,367x，函数在此区间上不单调，C错；65x

或6x时，函数值不存在，D错．故选：B．【一隅三反】1．（2020·辉县市第二高级中学高一期中）关于函数2tan(2)3yx，下列说法正确的是（）A．是奇函数B．在区间7(,)1212上单调递增C．(,0)12为其图象的

一个对称中心D．最小正周期为【答案】C【解析】22()1232，所以(,0)12是函数2tan(2)3yx图象的一个对称中心，故选C．2．（2020·海原县第一中学高一期末）下列关于函数πtan23yx

的说法正确的是（）A．在区间ππ,312上单调递增B．最小正周期是πC．图象关于点5π,012成中心对称D．图象关于直线π12x成轴对称【答案】C【解析】函数ππtan2tan

233yxx无单调递增区间和对称轴，A、D错误其最小正周期是2，故B错误πtan23yx在512x处无意义，故其图象关于点5π,012成中心对称，故C正确故选：C3．（2020·全国高一

课时练习）设函数tan23xfx.（1）求函数f(x)的最小正周期，对称中心；（2）作出函数fx在一个周期内的简图．【答案】（1）2T，2,03kkZ；（

2）图象见解析【解析】（1）tan23xfx，212T.令232xk，kZ，解得23xk，kZ，故对称中心为2,03kkZ.（2）令023x，解得23x，令234x，解得76x，令234x

，解得6x，令232x，解得53x，令232x，解得3x，所以函数tan23xfx的图象与x轴的一个交点坐标为2,03，在这个交点左右两侧相邻的渐近线方程分别为3x

和53x.故函数在一个周期内的函数图象为：