【文档说明】2021年高中数学人教版必修第一册：5.4《三角函数的图象与性质》精品讲义(原卷版).doc，共(10)页，739.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31038.html

以下为本文档部分文字说明：

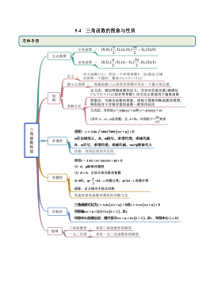
5.4三角函数的图象与性质思维导图常见考法考点一五点画图【例1】（1）（2020·全国高一课时练习）用五点法作出函数1cos(02)yxx的简图.（2）（2020·全国高一课时练习）利用正弦或余弦函数图象作出3sin2yx的图象．五点法画图作

形如y＝asinx＋b(或y＝acosx＋b)，x∈[0,2π]的图象时，可用“五点法”作图，其步骤是：①列表，取x＝0、π2、π、3π2、2π；②描点；③用光滑曲线连成图．【一隅三反】1．（2020·全国高一课时练习）利用“五点法”作出函数y＝1－sinx(0≤x≤2π)的简

图．2．（2020·全国高一课时练习）利用正弦曲线，求满足13sin22x的x的集合．3．（2020·武功县普集高级中学高一月考）用五点法作出函数32cosyx在0,2内的图像.考点二周期【例2】（1）（2020·福建高二学业考试）函数cos

yx的最小正周期为（）A．2B．C．32D．2（2）（2020年广东潮州）下列函数中，不是周期函数的是()A.y＝|cosx|B．y＝cos|x|C．y＝|sinx|D．y＝sin|x|【一隅三反】1．（2020·全国高一课时练习）下列函数中,最小正周期为的是()A．sin

yxB．cosyxC．sin2yxD．1cos2yx2．（2019·云南高二期末）函数()2sin36fxx的最小正周期为__________．考点三对称性【例3】（2020·辽宁大连

·高一期末）函数cos26fxx的图像的一条对称轴方程为（）A．6xB．512xC．23xD．23x【一隅三反】1．（2020·永昌县第四中学高一期末）函数y＝12sin3x

的图象的一条对称轴是（）A．x＝－2B．x＝2C．x＝－6D．x＝62．（2020·山西省长治市第二中学校高一期末（理））下列函数中，最小正周期为，且图象关于直线3x对称的函数是（）

A．2sin23yxB．2sin26yxC．2sin23xyD．2sin23yx3．（2020·河南平顶山·高一期末）如果函数

sin2yx的图象关于直线πx对称，那么取最小值时的值为（）A．3πB．π3C．π2D．2π考点四单调性【例4】（1）（2020·吉林扶余市第一中学高一期中）函数1πsin223fx

x的单调递增区间为（）A．5πππ,π1212kk，kZB．π3ππ,π44kk，kZC．2πππ,π36kk，kZD．πππ,π44kk，kZ（2）（2020·吉林扶余市第一中学高一期中）已知函数si

n2fxx在π0,6上单调递减，则实数的一个值是（）．A．3π2B．π2C．πD．2π【一隅三反】1．（2020·湖南益阳·高一期末）函数cos26fxx的单调递增区间为（）A．7,1212kkkZ

B．72,266kkkZC．5,1212kkkZD．52,266kkkZ2．（2020·全国高三其他（理））已知函数sin06fxx

，对任意xR，都有3fxf，并且fx在区间,63上不单调，则的最小值是（）A．1B．3C．5D．73．（2020·全国高三其他（理））函数cosfxx在0

,上为增函数，则的值可以是（）A．0B．2C．D．32考点五奇偶性【例5】（2020·上海黄浦·高一期末）下列函数中，周期是的偶函数为（）.A．cos2xyB．sin2yxC．|sin|y

xD．sin||yx【一隅三反】1．（2019·贵州高三月考（文））函数sin2yx是（）A．最小正周期为2的奇函数B．最小正周期为的奇函数C．最小正周期为2的偶函数D．最小正周期为的偶函数2．（2020·辽宁辽阳·高一期末）下列函数中，周期为的奇

函数是（）A．cos2xyB．sin(23)yxC．cos(2)yxD．cos2yx3．（2020·昆明市官渡区第一中学高一开学考试）已知函数3()sin42fxxxR，下面结论错误的是（

）A．函数()fx的最小正周期为2B．函数()fx在区间0,16上是增函数C．函数()fx的图象关于直线4x对称D．函数()fx是偶函数考点六定义域【例6】（1）（2020·宁县第二中学高一期中）函数1sin

yx的定义域是________.（2）（2020·宁县第二中学高一期中）函数2116sinyxx的定义域是__________.【一隅三反】1（2020·辽宁沈阳·高一期中）函数1tan24yx的定义域是（）A．4,2xxkkZ

∣B．2,2xxkkZ∣C．32,2xxkkZ∣D．,2xxkkZ∣考查函数的定义域，即求使函数有意义的取值范围．求函数定义域的依据(1)整式函数的定义域为R；(2)分式的分母不为零；(3)偶次根式的被开方数不小于零；

(4)对数函数的真数必须大于零；(5)正切函数y＝tanx的定义域为π{|π,}2xxkkZ；(6)x0中x≠0；(7)实际问题中除要考虑函数解析式有意义外，还应考虑实际问题本身的要求．2．（2020·湖南高一月考）函数3()=ln(sin-)2f

xx的定义域为（）A．2(,)()33kkkZB．5(,)()66kkkZC．2(2,2)()33kkkZD．5(2,2)()66kkkZ3．（2020·吉林公主岭·高

一期末（理））函数3ln(sincos)()3xxxfxx的定义域为（）A．0,3B．,43C．(,]43D．5,44考点七值域【例7】（1）

（2019·福建高三学业考试）函数2sinyx的最小值是。（2）（2020·全国高二月考（文））2cos38yx在区间,88上的最小值为______.（3）（2020·全国高一课时练

习）函数tanyx344x，且2x的值域是________________．【一隅三反】1．（2019·伊美区第二中学高一月考）求函数24sin4cos2yxx的最值，及取最值时x的集合．2．（2020·新疆高三三模（理）

）f(x)＝2sinωx(0<ω<1)，在区间0,3上的最大值是2，则ω＝________.3．（2020·山西省长治市第二中学校高一期末（理））已知函数()3sinfxx在区间[,]34上的最小值为3，则ω的

取值范围是（）A．9][6,)2(-,-B．93][,)22(-,-C．2][6,)(-,-D．32][,)2(-,-考点八正切函数性质【例8】（2020·山西省长治市第二中学校高一期末（理））下列关于函数πtan3yx

的说法正确的是（）A．函数的图象关于点π,03成中心对称B．函数的定义域为π{|π,Z}6xxkkC．函数在区间5π,66π上单调递增D．函数在区间5ππ[,]66上单调递增【一

隅三反】1．（2020·辉县市第二高级中学高一期中）关于函数2tan(2)3yx，下列说法正确的是（）A．是奇函数B．在区间7(,)1212上单调递增C．(,0)12为其图象的一个对称中心D．最小正周期为2．（2020·海原县第一中学高一期末）下列关于函数πt

an23yx的说法正确的是（）A．在区间ππ,312上单调递增B．最小正周期是πC．图象关于点5π,012成中心对称D．图象关于直线π12x成轴对称3．（2020·全国高一课时练习）设函数tan23xfx.（1）

求函数f(x)的最小正周期，对称中心；（2）作出函数fx在一个周期内的简图．