【文档说明】2021年高中数学人教版必修第一册：5.2《三角函数的概念》精品讲义(含解析).doc，共(14)页，1.014 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31254.html

以下为本文档部分文字说明：

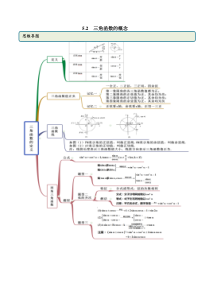
5.2三角函数的概念思维导图常见考法考点一三角函数的定义【例1】（1）（2020·全国高一课时练习）已知角的终边经过点(4,3)，则cos=（）A．45B．35C．35-D．45（2）（2020·甘肃省岷县第一中学高二月考）若角600°的终边上有一点（-4，a），则a的值是

（）A．43B．43C．43D．3（3）（2020·应城市第一高级中学高一月考）已知角α的终边上一点的坐标为（sin43，cos43），则角α的最小正值为（）A．76B．116C．56D

．43【答案】（1）D（2）C（3）A【解析】（1）∵已知角的终边经过点(4,3),∴224,3,5xyrxy．∴4cos5xr.故选：D．（2）∵角600的终边上有一点4,a，根据三角函数的定义可

得tan6004a，即4tan6004tan540604tan6043a，故选C.（3）由题意41sincos32，又4sin03，点(sin,cos)33在第三象限，

即是第三象限角，∴72,6kkZ，最小正值为76．故选：A．【一隅三反】1．（2020·辽宁沈河·沈阳二中高一期末）如果角的终边过点(2sin30,2cos30)P，那么sin等于（）A．12B．12C．32D

．33【答案】C【解析】由题意得(1,3)P，它与原点的距离为2，∴3sin2.故选：C.2．（2020·永州市第四中学高一月考）若一个角的终边上有一点4,Pa且3sincos4，则a的值为()A．43B．43C．－43或43

3D．3【答案】C【解析】由已知，得222222443sin,cos,4444aaaaa，解得43a或433，故选C．3．（2020·河南高一期末）已知点8,6cos60Pm在角的终边上，且3tan4

，则m的值为（）A．2B．2C．23D．23【答案】A【解析】16cos60632mmm，即点8,3Pm，由三角函数的定义可得33tan84m，解得2m.故选：A.考点二三角函数值正负判断【例3】（2020·辽宁高一期末）若si

ntan0，且cos0tan，则角是（）A．第一象限角B．第二象限角C．第三象限角D．第四象限角【答案】C【解析】2sinsintan0cos，cos0，又2coscos0tansi

n，则sin0.因此，角为第三象限角.故选：C.【一隅三反】1．（2020·大连市普兰店区第一中学高一月考）已知点tan,sinP在第三象限，则角的终边所在的象限为（）A．第一象限B．第二象

限C．第三象限D．第四象限【答案】D【解析】点tan,sinP在第三象限，tan0，sin0，由tan0，知角的终边所在的象限为第二象限或第四象限，由sin0，知角的终边所在的

象限为第三象限或第四象限，综上，角的终边所在的象限为第四象限.故选：D.2．（2020·昆明市官渡区第一中学高一月考）若－2<α<0，则点P(tanα，cosα)位于()A．第一象限B．第二象限C．第三象限D．第四象限【答案】B【解析】∵－2<α<0，∴tanα<0，cosα>0，

∴点P(tanα，cosα)位于第二象限，故选B3．（2020·山东滨州·高二期末）“为第一或第四象限角”是“cos0”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】当为第一或第四象限角时，cos0，所以“为第

一或第四象限角”是“cos0”的充分条件，当的终边在不同象限的时候，其三个三角函数值的符号也发生变化，记忆的口诀是“全正切余”即：第一象限全为正，第二象限正弦正，第三象限切为正，第四象限余弦正．当cos0时，为第一或第四象限角或x

轴正半轴上的角，所以“为第一或第四象限角”不是“cos0”的必要条件，所以“为第一或第四象限角”是“cos0”的充分不必要条件.故选：A考点三三角函数线【例3】（1）（2020·辽宁沈阳·高一期中）下列关系式中，正确的是（）A．sin1cos1ta

n1B．cos1sin1tan1C．tan1sin1cos1D．cos1tan1sin1（2）（2020·内蒙古通辽·高一期中（理））对于下列四个命题：①sinsin1810；②2517co

scos44；③tan138tan143；④tan40sin40.其中正确命题的序号是（）A．①③B．①④C．②③D．②④【答案】（1）B（2）B【解析】（1）画出1弧度的正弦线，余弦线和正切线，如图所示：则sin1,cos1,tan1MPOM

AT，比较,,OMMPAT的长度，得cos1sin1tan1.故选：B.（2）根据正弦函数的性质，可知：sinyx在,22上单调递增1810，sinsin1810，①正确；由诱导公式，

可得：2525coscos6cos4441717coscos4cos4442517coscos44

，②错误；根据正切函数的性质，可知：tanyx在,2ππ上单调递增，138143，tan138tan143，③错误；画出2409的正弦线和正切线，如下：tan40AT,sin40MP，所以tan40

sin40，故④正确.故选：B【一隅三反】1．（2019·重庆）sin4,cos4,tan4abc则,,abc的的大小关系是()A．abcB．bacC．acbD．cba【答案】A【解析】设4,则5π3π42,作出

角的三角函数线,如下图,则sin0MP,cos0OM,tan0AT,比较三角函数值大小常用的两种方法：（1）利用函数单调性；（2）利用三角函数线.又在OMP中,ππ,42MOP

,则MPOM,故sincos0tan,即sin4cos40tan4.故选:A.2．（2020·湖南长沙·高一月考）设sin1,cos1,tan1abc，则,,abc的大小关系

为（）A．abcB．acbC．cabD．cba【答案】C【解析】以O为圆心作单位圆，与x轴正半轴交于点A，作1POA交单位圆第一象限于点P，做PBx轴，作ATx轴交OP的延长线于点T，如下图所示：由三角函数线的定义知，cos1OB，sin1BP，tan1AT，因为π

π124，ATBPOB∴tan1sin1cos1∴cab故选：C3．（2019·伊美区第二中学高一月考）已知点(sincos,tan)P在第一象限，则在[0,2]内的取值范围是（）．A．35,,244

UB．5,,424C．353,,2442UD．3,,424【答案】B【解析】由已知点(sinco

s,tan)P在第一象限得：sincos0，tan0，即sincos，tan0，当sincos，可得52244kk，kZ．当tan0，可得222kk或3222kk，kZ．

2242kk或5224kk，kZ．当0k时，42或54．02剟，42或54．故选：B．考点四同角三角函数【例4】（1）（2020·镇原中学高一期末）若1sin2，π

(,π)2，则cos。（2）（2020·甘肃省岷县第一中学高二月考）已知tan3，32，那么cossin的值是。【答案】（1）32（2）132【解析】（1）因为1sin2，π(,π)2，所以13cos142.故选：B.（2）由题知

：22sin3cossincos1，解得3sin21cos2或3sin21cos2.因为32，所以3sin21cos2.所以13coss

in2.故选：B【一隅三反】1．（2020·衡阳市第二十六中学高一期末）已知4sin5=，并且是第二象限的角，那么tan的值等于（）A．43B．34C．34D．43【答案】A【解析】因为45sin，故231cos5c

os又因为是第二象限的角，故3cosα5故43sintancos.故选：A.2．已知3(,)22，且tan2，那么sinA．33B．36C．36D．33【答案】B【解析】因为3(,)22，sintan2cos

>0，故3(,)2即sin2cos，又22sincos1，解得：sin36故选：B3．（2020·河南项城市第三高级中学高一月考）若,2，且21cossin4，则tan

的值等于（）A．33B．33C．3D．3【答案】A【解析】由21cossin4可得241sin4sin10，即24sin4sin30，解得1sin2或3sin2（

舍）.,2，56，53tantan63.故选：A.考点五弦的齐次【例5】（2020·全国高一课时练习）已知tan2，求下列代数式的值．（1）4sin2cos5cos3sin；（2）22111sinsincoscos432．【

答案】（1）611；（2）1330.【解析】（1）4sin2cos4tan242265cos3sin3tan532511．（2）22111sinsincoscos432222

2111sinsincoscos432sincos22111tantan432tan12221112243211330【一隅三反】1．（2020·阜新市第二高级中学高一期末）已知tan2，则2sinco

ssin2cos的值为A．0B．34C．1D．54【答案】B【解析】2sincossin2cos21324tantan．2．（2020·大连海湾高级中学高一月考）已知s

in3cos53cossin，则2cossincos的值是（）．A．35B．35-C．3D．3【答案】A【解析】因为sin3cos53cossin，所以sin3coscos53cossincos

，即tan353tan，解得：tan2，所以22222sintacossincos1tan3cossincosc5nos1.故选：A.3．（2020·山西应县一中高一期中（理））已知tan1tan1，求下列各式的值.（1）

sin3cossincos；（2）2sinsincos2.【答案】（1）53；（2）135．【解析】由tan1tan1，解得1tan2．（1）sin3cossincos13tan3521tan1312

；（2）2sinsincos222222sinsincos2(sincos)sincos2222223sinsincos2cos3tantan2sincostan122113()2132215()12

．考点六sinacosa与sina±cosa【例6】（1）（2020·湖南衡阳·高一月考）若38sincos，且42，则cossin的值是A．12B．12C．14D．14（2）（2020·山东滨州·高二期末）已

知102sincos2，R，则tan（）A．13B．3C．13或3D．3或13【答案】（1）A（2）D【解析】（1）由42，则sincos，则21cossincossin12cossin2.故本题答案应选

A.（2）221052sincos4sin4sincoscos22Q22224sin4sincoscos5sincos22224tan4tan153tan8tan30tan12tan3或1tan3当1tan3

时，10310sincos1010，当tan3时，31010sincos1010，故选：D【一隅三反】1．（2020·科尔沁左翼后旗甘旗卡第二高级中学高一期末）如果1sincos5xx，且0πx，那么tanx的值是()A．43B．43或34C．34D．4

3或34【答案】A【解析】将所给等式两边平方，得12sincos25xx，∵0πx，sin,cos0xxs，249(sincos)12sincos25xxxx，9sincos5xx，∴434sin,

costan553xxx＝，.故选A.2．（2019·伊美区第二中学高一月考）已知1sincos5xx，且0πx，则sincosxx（）A．75B．75C．15D．15【答案】A【解析】因为1sincos5xx，故可得1122

5sinxcosx，解得12025sinxcosx.结合0x，故可得2x，故此时0cosx，0sinx，则0sinxcosx，且2497255sinxcosxsinxcosx.故

选：A.3．（2020·河南焦作·高二期末（理））已知,44，1sincos5，则tan（）A．34B．34或43C．34D．34或34【答案】A【解析】将1sincos5左右两边平方可得2

42sincos25.由2222sincos2tan242sincossincostan125，解得3tan4或43.∵,44，∴tan1,1，∴3tan4.故选：A