【文档说明】2021年高中数学人教版必修第一册：5.1《任意角和弧度制》精品讲义(含解析).doc，共(10)页，790.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31250.html

以下为本文档部分文字说明：

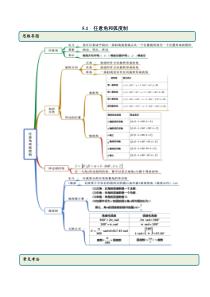
5.1任意角和弧度制思维导图常见考法考点一基本概念的辨析【例1】（2020·河南宛城·南阳中学高一月考）下列说法正确的个数是（）①小于90的角是锐角；②钝角一定大于第一象限角；③第二象限的角一定大于第一象限的角；④始边与终边重合的角为0.A．0B．1

C．2D．3【答案】A【解析】对①，小于90的角不是锐角，如10不是锐角，故①错；对②，390角是第一象限的角，大于任何钝角90180，故②错；对③，第二象限角中的210角小于第一象限角中的30角，故

③错；对④，始边与终边重合的角的度数是360kkZ，故④错．故选：A．【一隅三反】1．（2020·全国高一课时练习）下列说法正确的是（）A．终边相同的角一定相等B．钝角一定是第二象限角C．第四象限角一定是负角D．小于90的角都是锐

角【答案】B【解析】终边相同的角不一定相等，所以该选项错误；钝角一定是第二象限角，所以该选项正确；第四象限角不一定是负角，如116是第四象限的角，但是不是负角，所以该选项错误；小于90的角不都是锐角，如3

.所以该选项错误.故选B2．（2020·浙江高一课时练习）下列命题中正确的是（）．A．终边与始边重合的角是零角B．90°～180°间的角不一定是钝角C．终边和始边都相同的两个角相等D．第二象限的角大于第一象限的角【答案】B【解析】终边

与始边重合的角还有360°角，720°角等，故A错误；90°～180°间的角包括90°角，故90°～180°间的角不一定是钝角，故B正确；终边和始边都相同的两个角相差360,kkZ，故C错误；120°角是第二象限角，它小于第

一象限的角400°角，故D错误．故选：B3．（2020·陕西大荔·高一期末）下列说法正确的是（）A．第二象限角大于第一象限角B．不相等的角终边可以相同C．若是第二象限角，2一定是第四象限角D．终边在x轴正半轴上的角是零角【答案】B【解析】A选项，第一象限角36030120

，而120是第二象限角，∴该选项错误；B选项，36030与30°终边相等，但它们不相等，∴该选项正确；C选项，若是第二象限角，则222kkkZ，∴4242kkkZ

是第三象限角或第四象限角或终边在y轴负半轴上的轴线角，∴该选项错误；D选项，360角的终边在x轴正半轴上，但不是零角，∴该选项错误.故选：B.考点二角度与弧度的转换【例2】（2020·汪清县汪清第六中学高一期中（文））把下列各

角的弧度数化为度数，度数化为弧度数.（1）712；（2）136；（3）1125°；（4）-225°.【答案】（1）105；（2）390；（3）254；（4）54.【解析】根据弧度制与角度制的互化公式，1801,1180radrad，可得：（1）77180

1051212；（2）131366180390；（3）25112511251804rad；（4）52252251804rad.【一隅三反】1．（2020·全国高一课时练习）把下列角度化成弧度：（1）36；（2）150；

（3）1095；（4）1440.【答案】（1）5（2）56（3）7312（4）8【解析】（1）361805；（2）51501806；（3）73109518012；（4）14408180．2．（2020·甘肃城关·兰

州一中高一期中）315___________弧度,7π12弧度=________.【答案】7π4105【解析】18073153151804,77180π=1051212,

故答案为：7π4；1053．（2020·土默特左旗金山学校高一月考（理））下列转化结果错误的是（）A．30°化成弧度是6B．103化成度是600C．6730'化成弧度是27D．85化成度是288【答案】C【解析】30°化成弧度是6，A正确10

3化成度是600，B正确；6730'是367.567.51808，C错误；85化成度是288，D正确.故选：C.考点三终边相同【例3】（2020·全国高一课时练习）（1）把－1480°写成

2kkZ的形式，其中02；（2）在0,720内找出与25角终边相同的角.【答案】（1）16259；（2）72°，432°.【解析】（1）∵74148014801809

，而74161099，且02，∴169.∴161480259.（2）∵221807255，∴终边与25角相同的角为72360kkZ，当0k时

，72；当1k时，432.∴在0,720内与25角终边相同的角为72°，432°.【一隅三反】1．（2020·汪清县汪清第六中学高一期中（文））已知角2025.（1）将角改写成2k(kZ，02)的形式，并指出角是第几象限的角；

（2）在区间5,0上找出与角终边相同的角.【答案】（1）5104，是第三象限角；（2）19113,,444．【解析】（1）202545520251018044，54是第三象限角，∴是

第三象限角．（2）由55204k得25588k，因为kZ，∴3,2,1k，对应角依次为19113,,444．2．（2020·全国高一课时练习）把下列各角度化为弧度,并写成02的角加上2()kk

Z的形式.(1)64;(2)400;(3)72230【答案】(1)74245;(2)229;(3)143672.【解析】(1)16746424545;(2)202400299

;(3)144528914372230722.5621807272.3．（2019·陕西榆阳·榆林十二中高一月考）用弧度制写出角的终边在下图中阴影区域内的角的集合.（1）（2）【答案】（1）55{|22,}66xkxkkZ

；（2）{|,}42xkxkkZ【解析】（1）51506，51506，用弧度制表示终边在图中阴影区域内的角的集合为55{|22,}66xkxkkZ.（2）454，52254，用弧度制表示终边在图中

阴影区域内的角的集合为{|22,}42xkxkkZ53{|22,}42xkxkkZ{|,}42xkxkkZ.考点四象限的判断【例4】（2020·全国高一

课时练习）已知下列各角：①120②240③180④495，其中第二象限角的是（）A．①②B．①③C．②③D．②④【答案】D【解析】①120表示由x轴非负半轴绕原点顺时针旋转120，落在第三象限；②240表示由x轴非负半轴绕原点顺时针旋转240，落在第二象限；③180表示由x

轴非负半轴绕原点逆时针旋转180，落在x轴非正半轴；④495表示由x轴非负半轴绕原点逆时针旋转495，且495360135，495的终边和135的终边相同，所以落在第二象限.故选：D【一隅三反】1．（2020·周口市中英文学校高一期中）角2912的终边所在的象限是（）A．第一象限B．第二

象限C．第三象限D．第四象限【答案】A【解析】因为295=21212，角512是第一象限角，所以角2912的终边所在的象限是第一象限．故选A.2．（2020·全国高二）若是第二象限角，则180是()A．第一象限角B．第二象限

角C．第三象限角D．第四象限角【答案】A【解析】为第二象限角，不妨取120，则180为第一象限角，故选A．3．（2020·全国高一课时练习）在0°～360°范围内，找出与下列各角终边相同的角，并判定它们是第几象限角.（1）－

150°；（2）650°；（3）－950°15′.【答案】（1）210，第三象限的角；（2）290，第四象限的角；（3）12945，第二象限的角；【解析】（1）150360210，210是第三象限的角，150是第三象限的角；（2

）650360290，290是第四象限的角，650是第四象限的角；（3）95015108012945，12945是第二象限的角，95015是第二象限的角．考点五扇形【例5】（2020·浙江高一课时练习）已知一

扇形的圆心角为(0)，所在圆的半径为R.（1）若60，10Rcm，求扇形的弧长及该弧所在的弓形的面积；（2）若扇形的周长为20cm，当扇形的圆心角等于多少弧度时，这个扇形的面积最大?【答案】（1）103cm，2502533cm；（

2）2rad.【解析】（1）设扇形的弧长为l，弓形面积为S，则603，10R，101033lcm，2211035010102532343Scm.（2）设扇形弧长为l，则220lR，即1020

2101lRR，∴扇形面积2211(202)10(5)2522SIRRRRRR，∴当5Rcm时，S有最大值225cm，此时10lcm，2radlR.因此当2ra

d时，这个扇形面积最大.【一隅三反】1．（2020·赤峰二中）《九章算术》是我国古代的数学巨著，其中《方田》章给出了计算弧田面积所用的经验公式为：弧田面积12（弦×矢+矢2），弧田（如图阴影部分所示）是由圆弧和弦围成，公式中的

“弦”指圆弧所对的弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角为23，矢为4的弧田，按照上述方法计算出其面积是（）A．443B．843C．883D．81631.设扇形的半径为r，弧长为l，)20(

或n°为其圆心角，则弧长公式与扇形面积公式如下：类别/度量单位角度制弧度制扇形的弧长180rnlrl扇形的面积3602rnS22121rlrS12,2ClRSlR当周长C为定值时可得面积211222SCRRRCR当面积S为定值时可得周长

22SCRR.【答案】D【解析】设半径为r,圆心到弦的距离为d,则121cos232drr,11422rdrrr8,4rd所以弦长为2222641683rd,弧田面积为21834481

632.故选:D.2．（2020·辽宁沈阳·高一期中）一个半径是R的扇形，其周长为3R，则该扇形圆心角的弧度数为（）A．1B．3C．D．3【答案】A【解析】设扇形的弧长为l，则23RlR，得lR，则扇形圆心角的弧度数为1lR.故选：A.3．（20

20·上海高一课时练习）在扇形AOB中，半径等于r.（1）若弦AB的长等于半径，求扇形的弧长l；（2）若弦AB的长等于半径的3倍，求扇形的面积S【答案】（1）3r；（2）213r【解析】（1）如图所示：设AOB，若弦AB的长等于半径，则3所以扇形的弧长3lrr=?

（2）如图所示：若弦AB的长等于半径的3倍，则332sin2rACAOCOAr?==，因为0，所以3AOC，所以223AOC=?，所以扇形的面积为22111223Slrrr==?.