【文档说明】2021年高中数学人教版必修第一册：4.3《对数运算》精品讲义(含解析).doc，共(11)页，669.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31239.html

以下为本文档部分文字说明：

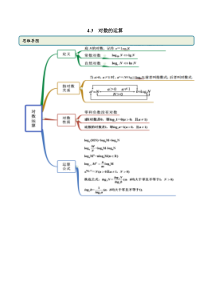
4.3对数的运算思维导图常见考法考点一指数对数的转化【例1】（2020·上海高一课时练习）将下列指数式与对数式互化.（1）31327；（2）3416x；（3）12log83；（4）log(12)1a.【答案】（1）31log32

7.（2）163log4x.（3）3182.（4）112a.【解析】因为由xab可得log,0,1,0axbaab，所以(1)由31327可得31log327；(2)由3416x可得163l

og4x；由log,0,1,0axbaab可得xab，所以(3)由12log83可得3182；(4)由log(12)1a可得112a.【一隅三反】1．（2020·全国高一课时练习）下列指数式与对数式互化不正确的一组是（）A．01e

与ln10B．13182与811log23C．3log92与1293D．7log71与177【答案】C【解析】01ln10e，故A正确；13182811log23，故B正确；23log9239，1291

93log32，故C不正确；17log7177，故D正确．故选：C．2．（2020·全国高一课时练习）将下列指数式写成对数式：（1）45625；（2）61264；（3）327a；（4）15.733m【答案】（1）5log6254

；（2）21log664；（3）3log27a；（4）13log5.73m【解析】（1）因为45625，所以5log6254.（2）因为61264，所以21log664.（3）因为327a，所以3log27a.

指数式和对数式的互化.由指数式转化为对数式时，以指数式的底数为底数，指数运算的结果为真数的对数，其结果为指数式的指数；由对数式转化为指数式时，以对数的底数为底数，对数运算的结果为指数的指数，其结果为对数式

的真数.（4）因为15.733m，所以13log5.73m.3．（2020·上海高一课时练习）将下列对数式改为指数式：（1）2log646，指数式为__________；（2）3log32，指数式为

__________；（3）lg1x，指数式为__________；（4）12log5x，指数式为____________.【答案】62642(3)3110x512x【解析】由于logbaNbaN，所以：（1）2log646，指数式为

6264；（2）3log32，指数式为2(3)3；（3）lg1x，指数式为110x；（4）12log5x，指数式为512x故答案为：6264；2(3)3；110x；512x.考点二对数式求值【例2】（2020·全国高一课时练习）

求下列各式中x的值：（1）642log3x；（2）log86x；（3）lg100x；（4）2lnex.【答案】（1）116；（2）2；（3）2；（4）2【解析】（1）因为642log3x所以2232331644416x.（2）因为log86x

,所以68x.又0x所以11136268222x（3）因为1g100x所以210100,1010xx于是2x（4）因为2lnex所以22ln,xexee于是2x【一隅三反】1．（2019·福建省仙游县枫亭中学高

一期中）下列四个等式:①lg(lg10)0;②lg(ln)0e;③若lg10x,则10x;④若lnex,则2xe.其中正确的是()A．①③B．②④C．①②D．③④【答案】C【解析】①lg(lg10)lg10;②lg(lne)lg10

;③若lg10x,则1010x;④若lnex,则exe.故选：C2．（2019·安徽金安·六安一中高一月考）已知log7[log3(log2x)]＝0，那么12x＝()A．13B．36C．33D．24【答案】D【解析】∵732log

loglog0x＝，∴32loglog1x，∴2log3x，∴8x．∴121248x．故选D．3．（2020·宁县第二中学高一月考）方程2log121x的解x__________【答案】12【解析】∵22log(12)1log2x，∴122x

，∴12x经检验12x满足120x故答案为：12.考点三对数式化简【例3】（1）（2020·湖北黄冈·高一月考）计算：2log3221lg2lg2lg5lg52log8_______.（2）（2020·山西应县一

中高二期中（文））计算：13021lg8lg25327e__________．（3）40433231log12log2log3log4(2)(31)2的值等于______．【答案】（1）2（2）4（3）112【解析】（1）原式()()21log3lg

2lg2lg5lg523=++-?()1lg2lg531123=+-?=+=.故答案为：2.（2）原式1333221lg21lg52lg2132lg52lg2lg52433

故答案为4（3）40433231log12log2log3log4(2)(31)2=3311112log2log222122．故答案为:112．【一隅三反】1．（2020·四川达州·高三其他（文））计算ln223

1lg2lg5(33)e______．【答案】0【解析】由题意1233ln22231lg2lg532lg2lg532lg10033e.故答案为：0.2．（2020·石嘴山市第三中学高二期末（理））494log4

327loglg25lg473______.【答案】154【解析】根据对数的运算性质及换底公式化简可得494log4327loglg25lg473773log44log4933loglg25473

711log42423log3lg1071152244，故答案为：154.3.log2748＋log212－12log242；【答案】－12【解析】原式＝log27×1248×42＝log2212＝－12.4.(lg2)3＋3lg2·lg

5＋(lg5)3.【答案】1【解析】原式＝(lg2＋lg5)[(lg2)2－lg2·lg5＋(lg5)2]＋3lg2·lg5＝(lg2)2＋2lg2·lg5＋(lg5)2＝(lg2＋lg5)2＝1.考

点四换底公式【例4】（2020·浙江高一课时练习）若,xyR，且2186xyxy，则xy为（）A．0B．1C．1或2D．0或2【答案】D【解析】令2186xyxyk，则2logxk，1

8logyk，6logxyk2186logloglogxykkk，依换底公式得lglglglg0lg2lg18lg6kkkk或lg2lg18lglg6k.当lg0k时，0x且0y，故0xy；当lg2lg18l

glg6k时，21811logloglglg2lg18xykkklg2lg18lg2lg18lg(218)lg2lg2lg18lg6lg2lg18k.故选：D【一隅三反】1．（2020·上海高一课时练习）2345

67log3log4log5log6log7log8_________.【答案】3【解析】原式2ln3ln4ln5ln6ln7ln8ln8log83ln2ln3ln4ln5ln6ln7ln2.故答案

为：3.2．（2018·江苏省连云港市锦屏高级中学高一期中）设lg2a，lg3b，则5log12等于（）A．21abaB．21abaC．21abaD．21aba【答案】D【解析】根据对数的换底公式得，5lg12lg3lg4lg32lg22log12lg5lg10l

g21lg21aba，故选D．3．（2020·浙江高一课时练习）计算：（1）257log5log7log16.（2）2539log3log3log5log5lg2.【答案】（1）4；（2）32.【解析】（1）257lg5lg7lg16lg16lo

g5log7log164lg2lg5lg7lg2.（2）2539log3log3log5log5lg2lg3lg3lg5lg5lg2lg2lg5lg3lg9lg3(lg2lg5)lg5(lg3lg9)lg

2lg2lg5lg3lg9lg32lg332lg32.考点五指数对数运算的综合【例5】（2020年广东湛江）（1）已知711,log473ab，试用,ab表示49log48.（2）若26a＝33b＝62

c，求证：1a＋2b＝3c.【答案】（1）492log482ba.（2）见解析【解析】（1）11lg3,73lg7aa.∵7log4,b∴lg4lg7b.则49lg48lg4lg32log48lg49lg72l

g722abab.（2）证明设26a＝33b＝62c＝k(k＞0)，那么6a＝log2k，3b＝log3k，2c＝log6k，∴1a＝6log2k＝6logk2，1b＝3log3k＝3logk3，1c＝2log6k＝2lo

gk6.∴1a＋2b＝6·logk2＋2×3logk3＝logk(26×36)＝6logk6＝3×2logk6＝3c，即1a＋2b＝3c.【一隅三反】1．（2019·浙江南湖·嘉兴一中高一月考）若实数a，b满足3412

ab，则11ab（）A．12B．15C．16D．1【答案】D【解析】因为3412ab，所以34log12,log12ab，121212341111log3log4log1211212abloglog．故选：D．2．（2020·浙江高二月考）若32

a，2log3b，则ab________，22bb________．【答案】1103【解析】因为32a，所以3log2a，又2log3b，所以32lg2lg3log2log31lg3lg

2ab，22log3log31102232323bb.3．（2020·定远县育才学校高一月考）已知log189＝a，18b＝5，则log3645=（）A．22aB．2abC．2abaD．2aba【答案】D【解析】由1

85b得18log5b，18181818362181818log45log(59)log5log9log4518log362log92log9baa．故选：D．