【文档说明】2021年高中数学人教版必修第一册：1.5《全称量词与存在量词》精品讲义(含解析).doc，共(10)页，570.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31195.html

以下为本文档部分文字说明：

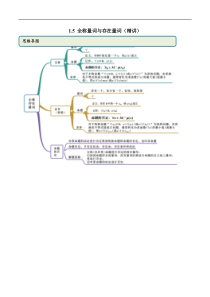
1.5全称量词与存在量词（精讲）思维导图考点一全称命题的判断【例1】（2020·全国高一课时练习）下列命题含有全称量词的是（)A．某些函数图象不过原点B．实数的平方为正数常见考法C．方程2250xx有实数解D．素数中只有一个偶数【答案】B【解析

】“某些函数图象不过原点”即“存在函数，其图象不过原点”；“方程2250xx有实数解”即“存在实数x，使2250xx”；“素数中只有一个偶数”即“存在一个素数，它是偶数”，这三个命题都是存在量词命题，“实数的平方为正数”即“所有的实数，它的平方为正数”，是全称

量词命题，其省略了全称量词“所有的”，所以正确选项为B.【一隅三反】1．（2020·全国高一）下列语句不是全称量词命题的是（）A．任何一个实数乘以零都等于零B．自然数都是正整数C．高一(一)班绝大多数同学是团员D．每一个实数都有大小【答案

】C【解析】A中命题可改写为：任意一个实数乘以零都等于零，故A是全称量词命题；B中命题可改写为：任意的自然数都是正整数，故B是全称量词命题；C中命题可改写为：高一(一)班存在部分同学是团员，C不是全称量词命题；D中命题可改写为：任意的一个实数

都有大小，故D是全称量词命题．故选：C.2．（2020·全国高一单元测试）（多选）下列命题中，是全称量词命题的有（）A．至少有一个x使2210xx成立B．对任意的x都有2210xx成立C．对任意的x都

有2210xx不成立D．存在x使2210xx成立E.矩形的对角线垂直平分【答案】BCE【解析】A和D中用的是存在量词“至少有一个”“存在”，属存在量词命题；B和C用的是全称量词“任意的”，属全称量词命题，所以B、C是全称量词命题；E中

命题“矩形的对角线垂直平分”省略量词“任意”，是全称量词命题.故选：BCE考点二特称命题的判断【例2】（2020·全国高一）指出下列命题是全称量词命题还是存在量词命题，并判断它们的真假.由全称命题的定义，全称命题应包含

所有，任意的„等表示全部元素都满足的语句（1）∀x∈N，2x＋1是奇数；（2）存在一个x∈R，使11x＝0；（3）对任意实数a，|a|＞0；【答案】（1）是全称量词命题；是真命题；（2）是存在量词命题；是假命题；（3）是全称量词命题；是假命题.

【解析】（1）是全称量词命题.因为,21xNx都是奇数，所以该命题是真命题.（2）是存在量词命题.因为不存在xR，使101x成立，所以该命题是假命题.（3）是全称量词命题.因为00，所以||0a不都成立，因此，该命题是

假命题.【一隅三反】1．（2020·全国高一课时练习）下列命题中：①有些自然数是偶数；②正方形是菱形；③能被6整除的数也能被3整除；④对于任意xR，总有2111x„；存在量词命题的个数是（）A．0B．

1C．2D．3【答案】B【解析】命题①中含有存在量词，是存在量词命题；命题②中全称量词省略，可以叙述为“所有的正方形都是菱形”，是全称量词命题；命题③中全称量词省略，可以叙述为“一切能被6整除的数也都能被3整除”，是全称量词命题；而命题④中有全称量词“总有”，是全称量词命题故有1个存在量词命

题；故选：B.2．（2020·全国高一课时练习）下列命题不是存在量词命题的是（）A．有的无理数的平方是有理数B．有的无理数的平方不是有理数C．对于任意xZ，21x是奇数D．存在xR，21x是奇数【答案】C【解析】A、B、D中都有存在

量词，是存在量词命题，C中含有量词“任意”，为全称量词命题，故选：C.考点三全称、特称命题真假的判断【例3】（2020·全国高一课时练习）判断下列命题是全称量词命题还是存在量词命题，然后写出对应的否定命题，并判

断真假:(1)不论m取何实数,关于x的方程20xxm必有实数根；(2)所有末位数字是0或5的整数都能被5整除；(3)某些梯形的对角线互相平分；(4)函数ykx图象恒过原点.【答案】见解析【解析】(1)即“所有mR，关于x的方程20xxm

都有实数根”，是全称量词命题，其否定为“存在实数m，使得方程20xxm没有实数解”，真命题；(2)是全称量词命题，其否定为“存在末位数字是0或5的整数不能被5整除”，假命题；(3)是存在量词命题，其否定为“所有梯形的对角线不互相平分”，真命题；(4)即“所有k

R，函数ykx图象都过原点”，是全称量词命题，其否定为“存在实数k，使函数ykx图象不过原点”，是假命题.【一隅三反】1．（2020·平罗中学高二期末（文））下列是全称命题且是真命题的是()A．∀x∈R，x2>0B．∀x∈Q，x2∈QC．∃x0∈Z，x20>1D．∀x

，y∈R，x2＋y2>0【答案】BA、B、D中命题均为全称命题，但A、D中命题是假命题．故选B．2．（2020·全国高一课时练习）关于命题“当1,2m时，方程220xxm没有实数解”，下列说法正确的是（)A．是全称量词命题，假命题B．是全称量词命题，真命题C．是存在

量词命题，假命题D．是存在量词命题，真命题【答案】A【解析】原命题的含义是“对于任意1,2m，方程2x2xm0都没有实数解”，但当1m时，方程有实数解1x，故命题是含有全称量词的假命题，所以正确选项为A.3．（2020·全国高一）用符号“”与

“”表示下列含有量词的命题,并判断真假：(1)任意实数的平方大于或等于0；(2)对任意实数a，二次函数2yxa的图象关于y轴对称；(3)存在整数x，y，使得243xy；(4)存在一个无理数，它的立方是

有理数.判断命题是特称命题还是全称命题，要注意补上省略词，同时注意判断命题为假命题时，只要能举出反例即可.【答案】(1)2,0xRx….真命题；(2)aR,二次函数2yxa的图象关于y轴对称,真命题；(3),,243xZyZxy假命题；(4

)3,RxQxQð，真命题.【解析】(1)2,0xRx，是真命题；(2)aR,二次函数2yxa的图象关于y轴对称,真命题，；(3),,243xZyZxy假命题,因为242(2)xyxy

必为偶数；(4)3,RxQxQð.真命题,例如332,2xxQ.考点四命题的否定【例4】（2020·全国高一课时练习）设A是奇数集，B是偶数集，则命题“xA，2xB”的否定是（)A．xA，2xBB．xA，2xBC．xA，2

xBD．xA，2xB【答案】A【解析】“xA，2xB”即“所有xA，都有2xB”，它的否定应该是“存在xA，使2xB”，所以正确选项为A.【一隅三反】1．（2020·全国高一课时练习）下列命题的否定为假命题的是（）A．xZ，14

3xB．xZ，510xC．xR，210xD．xR，2320xx【答案】D【解析】对A，命题的否定为假命题等价于该命题是真命题，由143x得1344x，这样的整数x不全称(存在性)命题进行否定的两步操作：①找到命题所含

的量词，没有量词的要结合命题的含义加上量词，再进行否定；②对原命题的结论进行否定.存在，故A为假命题，其否定为真命题，故A错误；对B，510x，15xZ，故B为假命题，其否定为真命题，故B错误；对C，210x1

x，故C为假命题，其否定为真命题，故C错误；对D，存在1x或2x，使232(1)(2)0xxxx，故D为真命题，从而D的否定是假命题，故D正确.故选：D.2．（2020·湖南天心.长郡中学高三其他（文））已知命题:pxR，2230xx，则命题p的否定

是（）A．xR，2230xxB．xR，2230xxC．xR，2230xxD．xR，2230xx【答案】C【解析】命题p为特称命题，其否定为:pxR，2230xx.故选：C.3．（2019·银川唐徕回民中学高三月考（理））命题

“2,240xRxx”的否定为（）A．2,240xRxxB．2000,240xRxxC．2,240xRxxD．2000,240xRxx【答案】B【解析】根据全称命题的否定是特称命题，将全称量词换为存在量词，不等号换为

＞，可得命题“2,240xRxx”的否定为“2000,240xRxx”，故选：B.考点五全称特称求参数【例5】（1）（2020·湖南雁峰.衡阳市八中高二期中）命题“1,2x，20xa”为真命题的一个充分不必要条件是（）A．4aB．5aC．3aD．5a（2）（

2020·浙江高一课时练习）若命题“xR，使21()10xax＋－＋”是假命题，则实数a的取值范围为()A．13aB．13a－C．33a－D．11a－（3）（2019·四川省绵阳南山中学高三月

考（理））已知函数2()2fxxx，()2(0)gxaxa，若1[1,2]x，2[1,2]x，使得12()()fxgx，则实数a的取值范围是()A．1(0,]2B．[0,3]C．(0,3]D

．[3,)【答案】（1）B（2）B（3）D【解析】（1）1,2x，214x，∴要使20xa恒成立，则2ax恒成立，即4a，本题求的是充分不必要条件，结合选项，只有B符合.故选：B.（2）由题得，原命题的否命题是“xR，

使21()10xax＋－＋”，即2(1)40a，解得13a－．选B.（3）由22()211fxxxx，知当1[1,2]x时，1()1,3fx由()2(0)gxaxa，知当21,2x时，2()2,22gxaa

由题意得：1,32,22aa，即21223aa，解得3a综上，3a.故选：D【一隅三反】1．（2020·浙江高一课时练习）若命题“2,10xRxax”是真命题，

则实数a的取值范围是（）.1.含参数的一元二次不等式的恒成立问题，优先考虑参变分离的方法，把问题归结为不含参数的函数的值域问题，也可以讨论不等式对应的二次函数的最值.2.求解含有量词的命题中参数范围的策略(1)对于全称命

题“∀x∈M，a>f(x)(或a<f(x))”为真的问题，实质就是不等式恒成立问题，通常转化为求函数f(x)的最大值(或最小值)，即a>f(x)max(或a<f(x)min)．(2)对于特称命题“∃x0∈M，a>f(x0)

(或a<f(x0))”为真的问题，实质就是不等式能成立问题，通常转化为求函数f(x)的最小值(或最大值)，即a>f(x)min(或a<f(x)max)．A．2{|}2aaB．2{2}|aaa或C．2{|2}aaD．2{}2|aaa或【答案】B【解析】命题“2,

10xRxax”是真命题，则需满足240a，解得2a或2a.故选：B.2．（2020·全国高一课时练习）命题“已知1yx，xR都有my”是真命题，则实数m的取值范围是（)A．1mB．1mC．1m

D．1m【答案】C【解析】由已知1yx，得1y，要使xR，都有my成立，只需1m，所以正确选项为C.3．（2020·广东高三其他（文））已知命题2000:,20pxRxxa，命题1:0,qx

xax，若p假q真，则实数a的取值范围为（）A．(1,)B．(,2]C．(1,2)D．(1,2]【答案】C【解析】命题0:pxR，20020xxa为假命题，则2,20xRxxa为真命题，满足2240a，解得1a；命题1:0,q

xxax为真命题，由1122xxxx，当且仅当1x时等号成立，可知2a，故实数a的取值范围为(1,2)，故选：C.4．（2019·四川省绵阳南山中学高三月考（理））已知函数2,1()1,1xaxxfxaxx，若1212,,xxRxx，使

得12()()fxfx成立，则实数a的取值范围是___________.【答案】(,2)【解析】函数2yxax的对称轴为=2ax，当12a即2a时，2yxax在,1上不是单调函数，则()fx在R上也不是单

调函数，满足题意；当12a即2a时，分段函数为R上的单调增函数，不满足题意.故答案为：(,2)