【文档说明】2021年高中数学人教版必修第一册：1.4《充分、必要条件》精品讲义(含解析).doc，共(8)页，540.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31191.html

以下为本文档部分文字说明：

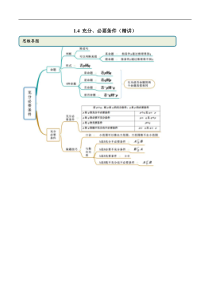
1.4充分、必要条件（精讲）思维导图考法一命题及其判断【例1】（1）（2020·全国高一课时练习）下列语句为命题的是（）A．250xB．求证对顶角相等C．0不是偶数D．今天心情真好啊常见考法（2）（2020·全国高一课时练习）命题“三角形

中，大边对大角”，改成“若p，则q”的形式，则（)A．三角形中，若一边较大，则其对的角也大，真命题B．三角形中，若一边较大，则其对的角也大，假命题C．若一个平面图形是三角形，则大边对大角，真命题D．若一个平面图形是三角形，则大边对大角，假命题【答案】（1）C（2）A）【解

析】（1）对于A选项，250x为不等式，不能判定真假，故不是命题；对于B选项，“求证对顶角相等”为操作命令；对于D选项，为感叹句，不是命题.故选：C.（2））命题中“三角形中”是大前提，条件应该是“大边”，结

论是“对大角”，所以正确选项为A.【一隅三反】1．（2019·宁波市第四中学高二期中）命题“若a，b都是奇数，则ab是偶数”的逆否命题是（）A．若两个整数a与b的和ab是偶数，则a，b都是奇数B．若两个整数a

，b不都是奇数，则ab不是偶数C．若两个整数a与b的和ab不是偶数，则a，b都不是奇数D．若两个整数a与b的和ab不是偶数，则a，b不都是奇数【答案】D【解析】由逆否命题定义可知：命题“a，b都是奇数，则ab是偶数”的逆否命题是：“若ab不是偶数，则a，b不都是奇数”．故选：D

．2．（2020·全国高三专题练习（文））命题“若21x＜，则11x＜＜”的逆否命题是（）A．若21x，则1x，或1xB．若11x，则21xC．若1x，或1x，则21xD．若1x或1x，则21x【答案】D【解析

】命题“若21x＜，则11x＜＜”的逆否命题是“若1x或1x，则21x”.1.命题的判断：（1）陈述句（2）可以判断对错2.命题的一般形式：若p则q3.命题的逆命题、否命题、逆否命题的改写时，先把原命题改成

若p则q故选：D.3．（2020·黑龙江高二期末（文））若1x，则0x的否命题是（）A．若1x，则0xB．若1x，则0xC．若1x，则0xD．若1x，则0x【答案】C【解析】“若1x，则0x”的否命题是“若1x

，则0x”.故选：C.考法二充分、必要条件【例2】（1）（2019年天津市高考数学试卷（理科））设xR，则“250xx”是“|1|1x”的()A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充

分也不必要条件（2）（2019安徽省合肥市第一中学）不等式22530xx成立的一个充分不必要条件是（）A．0xB．0x或2xC．2xD．12x或3x【答案】（1）B（2）C【解析】（1）化简不等式，

可知05x推不出11x；由11x能推出05x，故“250xx”是“|1|1x”的必要不充分条件，故选B．（2）解不等式22530xx，得3x或12x，结合四个选项，D是其充要条件

，AB是其既不充分也不必要条件，C选项2x是其充分不必要条件.故选：C.【一隅三反】1.（北师大版新教材2.1必要条件与充分条件）设集合1,Aa，1,2,3B，则“3a”是“BA”的（)A．充分条件B．必要条件C．没有充分、必要性D．既是充分又是必要条件【

答案】A【解析】当3a，集合1,3A，1,2,3B，所以BA正确，即“3a”是“BA”的充分条件，所以正确选项为A.2．（2020届山东省烟台市高考诊断性测试）设xR，则“|2|1x”是“2

230xx”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】|2|1x，解得13x，2230xx，解得3x或1x，“13x”成立，则“3x或1x

”成立，而“3x或1x”成立，“13x”不一定成立，所以“|2|1x”是“2230xx”的充分不必要条件.故选：A3．若集合|0Axx，下列各式是“aA”的充分不必要条件的是（)A．1aB．1a

C．0aD．0a【答案】B【解析】集合|0Axx，当1a时，aA，反之不成立，即为充分不必要条件，所以正确选项为B.考法三求参数【例3】（《2020年高考一轮复习讲练测》）已知:|1|2px，:qxa，且p是q的充分

不必要条件，则a的取值范围是（）A．1aB．3aC．1aD．1a【答案】D【解析】由题意知：:|1|2px可化简为{|31}xxx或，:qxa，所以q中变量取值的集合是p中变量取值集合的真子集，所以1a.【一隅三反】1“关于x的

不等式2x2axa0的解集为R”的一个必要不充分条件是()利用原命题与其逆否命题的等价性，对p是q的充分不必要条件进行命题转换，使问题易于求解.A．0a1B．10a3C．0a1D．a0或1a3【答案】C【解析】因为关于x的不等式220xaxa的解集为R，

所以函数2()2fxxaxa的图象始终落在x轴的上方，即2440aa，解得01a，因为要找其必要不充分条件，从而得到(0,1)是对应集合的真子集，对比可得C选项满足条件，故选C.2．已知1:12px，:||2qxa，若p是q的充分不必要条件，则实数a的取值范围为（）A．

(,4]B．[1,4]C．(1,4]D．(1,4)【答案】C【解析】由112x，即302xx，解得23x，由||2xa得22axa，若p是q的充分不必要条件，则2223aa，解得14a，实数a的取值范围为1,4，故选：C.3．（河南省高中毕业班

阶段性测试（四）理科数学试）关于x的不等式30xax成立的一个充分不必要条件是11x，则a的取值范围是（）A．1aB．0aC．2aD．1a【答案】D【解析】由题可知1,1是不等式30xax的解集的一个真子集.当3a时，

不等式30xax的解集为3xx，此时1,13xx；当3a时，不等式30xax的解集为,3,a，1,1,3，合乎题意；当3

a时，不等式30xax的解集为,3,a，由题意可得1,1,a，此时13a.综上所述，1a.故选：D.考法四充分性必要性的证明【例4】（2020年【衔接教材暑假作业】初高中衔接数学）已知,xy都是非零实数，且xy，求证：11xy的充

要条件是0xy.【答案】见解析【解析】（1）必要性：由11xy，得11xy，即0yxxy，又由xy，得0yx，所以0xy.（2）充分性：由0xy及xy，得xyxyxy，即11xy.综上所述，11xy的充要条件是0xy【一隅三反】1．（2020年【衔接教材暑假作业

】初高中衔接数学（新人教版））求证：关于x的方程210xmx有两个负实根的充要条件是2m．【答案】详见解析【解析】充分性：2m，240m，方程210xmx有实根，设210xmx的两根

为1x，2x，由韦达定理知：1210xx，1x、2x同号，又122xxm，1x，2x同为负根；必要性：210xmx的两个实根1x，2x均为负，且121xx，121112()22mxxxx22111112101xxxxx

，2m．所以命题得证．2．求证：一元二次方程ax2＋bx＋c＝0有一正根和一负根的充要条件是ac<0.【答案】见解析．【解析】(1)必要性：因为方程20axbxc有一正根和一负根，所以240bac为12120(,cxxxxa方程的两根)，所以a

c<0.(2)充分性：由ac<0可推得Δ＝b2－4ac>0及x1x2＝<0(x1，x2为方程的两根)．所以方程ax2＋bx＋c＝0有两个相异实根，且两根异号，即方程ax2＋bx＋c＝0有一正根和一负根．综上所述，一元二次方程ax2＋bx＋c＝0有一正根和一负根的充要条件是ac<0.