【文档说明】2021年高中数学人教版必修第一册：2.1《等式与不等式的性质》精品讲义(原卷版).doc，共(8)页，368.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31140.html

以下为本文档部分文字说明：

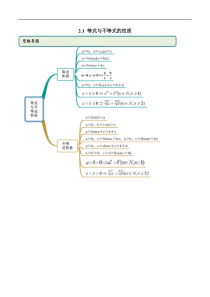
2.1等式与不等式的性质思维导图常见考法考点一等式性质【例1】（2019·全国高一课时练习）下列变形中错误的是（）A．若xy，则55xyB．若xyaa，则xyC．若33xy，则xyD．若xy，则xymm【一隅三反】1．（2019·全国高一课时练习）根据等

式的性质判断下列变形正确的是（）A．如果23x，那么23xaaB．如果xy，那么55xyC．如果162x，那么3xD．如果xy，那么22xy2．（2019·全国高一课时练习）若ab，则下列变形正确的是（）A．33abB．22abC．55ab

D．0ab考点二不等式性质【例2】（2020·河北省曲阳县第一高级中学高一期末）对于任意实数a，b，c，则下列四个命题：①若ab，0c，则acbc；②若ab，则22acbc；③若22acbc，则ab

；④若ab，则11ab.其中正确命题的个数为（）A．3B．2C．1D．0【一隅三反】1．（2020·上海高一开学考试）下列命题正确的是（）A．若>ab，则11abB．若>ab，则22abC．若>ab，cd，则>acbdD．若>ab，>cd，则>acbd2

．（2020·全国高一开学考试）若a、b、c为实数，则下列命题正确的是（）A．若ab，则22acbcB．若0ab，则22aabbC．若0ab，则11abD．若0ab，则baab3．（2020·武汉外国语学校高一月考）下列结论正

确的是（）A．若ab，则11baB．若22ab，则abC．若ab，cd则adbcD．若ab，则22acbc考点三比较大小本题考查不等式正误的判断，常用的判断方法有：不等式的基本性质、特殊值法以及比较法【例3】（2020·全国高一课时练习）已知a，b均为正实数

，试利用作差法比较33ab与22abab的大小.【一隅三反】1．（2020·全国高一课时练习）已知，那么,,,abab的大小关系是（）A．abbaB．ababC．abbaD．abab2．（2020·浙江高一课时练习）设2,

73,62abc，则,,abc的大小关系为（）．A．abcB．acbC．bacD．bca一．作差法、作商法是比较两个实数（或代数式）大小的基本方法．①作差法的步骤：作差、变形、判断差的符号、得出结论．②作商法的步骤：

作商、变形、判断商与1的大小、得出结论．二．介值比较法也是比较大小的常用方法，其实质是不等式的传递性：若a＞b，b＞c，则a＞c；若a＜b，b＜c，那么a＜c．其中b是介于a与c之间的值，此种方法的关键是通过

恰当的放缩，找出一个比较合适的中介值．三．比较大小时应注意：（1）比较代数式的大小通常采用作差法，如果含有根式，也可以先平方再作差，但此时一定要保证代数式大于零；（2）作差时应该对差式进行恒等变形（如配方、因式分解、有

理化、通分等），直到能明显看出其正负号为止；考点四代数式的取值范围【例4】(1)（2019·广东高考模拟（理））已知11xy，13xy，则182yx的取值范围是（）A．82,2B．81,22C．72,2D．71,22(2)（201

9·浙江绍兴一中高一月考）已知实数x，y满足41xy，145xy，则9xy的取值范围是（）A．[7,26]B．[1,20]C．[4,15]D．[1,15]【一隅三反】1．（2020·安徽金

安.六安一中高一期中（文））已知二次函数()yfx的图象过原点，且1(1)2,3(1)4ff，则(3)f的取值范围为（）A．[6,10]B．[21,30]C．3963,22D．[4,12]

2．（2020·山东济宁.高一月考）若25,310ab，则2ab的范围为_______________3．（2019·全国高一课时练习）已知26xy，34xy，则2256xxyy的值为______

______.考点五不等式证明【例5】（2020·全国高一课时练习）已知0ab，0c，求证：ccab.代数式的取值范围的一般思路：（1）借助性质，转化为同向不等式相加进行解答；（2）借助所给条件整体使用，切不可随意拆分所给条件；（3）结合不等式的

传递性进行求解【一隅三反】1．（2020·全国高一课时练习）证明不等式22222abab(,abR).2．（2020·全国高一课时练习）如果0ab，0cd，证明：acbd.3．（

2020·全国高一）已知0abcd，adbc．（Ⅰ）证明：adbc；（Ⅱ）证明：abcbcaabcabc．