【文档说明】2021年高中数学人教版必修第一册：5.7《三角函数的应用》精品讲义(原卷版).doc，共(5)页，332.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31080.html

以下为本文档部分文字说明：

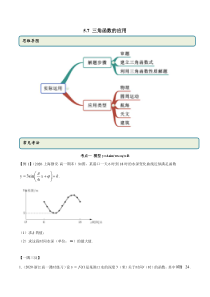
5.7三角函数的应用考点一模型y=Asin(wx+ψ)+B【例1】（2020·上海静安·高一期末）如图，某港口一天6时到18时的水深变化曲线近似满足函数3sin6yxk.（1）求k的值；（2）求这段时间水深（单位：m）的最大值.【一隅三反】1．（2020·浙江高一课

时练习）设()yft是某港口水的深度y（米）关于时间t（时）的函数，其中024t剟.思维导图常见考法下表是该港口某一天从0时至24时记录的时间t与水深y的关系：/t时03691215182124/y米1215.112.19.111.914.911.98.912.1经长期观察，函数()y

ft的图像可以近似地看成函数sinykAt的图像.下面的函数中，最能近似表示表中数据间对应关系的函数是（）A．123sint,[0,24]6ytB．123sin,[0,24]6yttC．123sint,[0,24]12yt

D．123sin,[0,24]122ytt2．（2020·新乡市第一中学高一月考）海水具有周期现象，某海滨浴场内水位y（单位：m）是时间t（024t，单位：h）的函数，记作yf

t，下面是某天水深的数据：t03691215182124y21.511.521.511.52经长期观察，yft的曲线可近似的满足函数sinyAtb.（1）根据以上数据，求出函数yft一个近似表达式；（2）一般情况下，水深超过1.25米该海滨浴场方可开放，另外，当水深超

过1.75米时，由于安全原因，会被关闭，那么该海滨浴场在一天内的上午7:00到晚上19:00，有多长时间可以开放?考点二圆周运用【例2】（2020·浙江高一课时练习）如图，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针尖位

置(,)Pxy.若初始位置为031(,)22P，当秒针从0P（注此时0t）正常开始走时，那么点P的纵坐标y与时间t的函数关系为A．ππsin()306ytB．ππsin()606ytC．ππsin()306ytD．ππsin()303yt【一隅三反】1．（2020·浙

江高一课时练习）一观览车的主架示意图如图所示，其中O为轮轴的中心，距地面32m(即OM长)，巨轮的半径长为30m，AM＝BP＝2m，巨轮逆时针旋转且每12分钟转动一圈．若点M为吊舱P的初始位置，经过t分钟，该吊舱

P距离地面的高度为h(t)m，则h(t)等于()A．30sin122t＋30B．30sin62t＋30C．30sin62t＋32D．30sin62t2．（2020·株洲市九方中学月考）随着机动车数量的增加，

对停车场所的需求越来越大.如图，ABCD是一块边长为100米的正方形地皮，其中ATPS是一座半径为90米的扇形小山，P是弧TS上一点，其余部分都是平地，现一开发商想在平地上建一个边落在BC和CD上的长方形停车

场PQCR.（1）设PAB，试写出停车场PQCR的面积S与的函数关系式；（2）求长方形停车场PQCR面积的最大值和最小值（数据精确到个位）.（注：当π02时，sincos1,2

）3．（2020·河南宛城·南阳中学高一月考）如图，已知OPQ是半径为1，圆心角为3的扇形，点A在弧PQ上（异于点,PQ)，过点A做,ABOPACOQ，垂足分别为,BC，记AOB，四边形ACOB的

周长为l.（1）求l关于的函数关系式；（2）当为何值时，l有最大值，并求出l的最大值.