【文档说明】《因式分解法》教学设计1-九年级上册数学苏科版.doc，共(2)页，50.000 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-26158.html

以下为本文档部分文字说明：

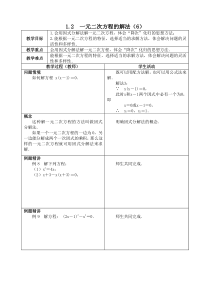
1.2一元二次方程的解法（6）教学目标1.会用因式分解法解一元二次方程，体会“降次”化归的思想方法；2.能根据一元二次方程的特征，选择适当的求解方法，体会解决问题的灵活性和多样性．教学重点会用因式分解法解一元二次方程，体会

“降次”化归的思想方法．教学难点能根据一元二次方程的特征，选择适当的求解方法，体会解决问题的灵活性和多样性．教学过程（教师）学生活动问题情境如何解方程x(x－1)＝0．既可以用配方法解，也可以用公式法来解．解

法3：∵x(x－1)＝0，此时x和x－1两个因式中必有一个为0，即x＝0或x－1＝0，∴x1＝0，x2＝1．概念这种解一元二次方程的方法叫做因式分解法．如果一个一元二次方程的一边为0，另一边能分解成两个一次因式的乘积，那么这样的一元二次方程就可用因式分解法来求解．明

确因式分解法的概念．例题精讲例8解下列方程：（1）x2＝4x；（2）x＋3－x(x＋3)＝0．师生共同完成．例题精讲例9解方程：(2x－1)2－x2＝0．师生共同完成．观察与思考解方程：(x＋2)2＝4（x＋2）．思考：哪种解法正确？你是怎样思

考的？解法1：原方程可变为(x＋2)2－4(x＋2)＝0，(x＋2)(x－2)＝0．x＋2＝0或x－2＝0．所以x1＝－2，x２＝2．解法2：原方程两边都除以（x＋2），得x＋2＝4．所以x＝2．达标练习课本练习P19练习1、2．学生课内完

成．总结1.用因式分解法解一元二次方程的一般步骤：（1）把一元二次方程右边化为0；（2）将方程左边分解为两个一次因式的积；（3）每个因式分别为0，得到两个一元一次方程；（4）解这两个一元一次方程，它们的解就是原方程的解．2.一元二次方程的根有几种情况？对本节内容进行归纳、总结．课后作业

①课本习题1.2，P20第5题；②适当补充针对性练习．完成作业，及时反馈．