【文档说明】《3.1 勾股定理》PPT课件1-八年级上册数学苏科版.ppt，共(26)页，1.858 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-25924.html

以下为本文档部分文字说明：

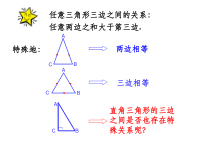
直角三角形的三边之间是否也存在特殊关系呢？任意三角形三边之间的关系：特殊地：两边相等三边相等ABCACBCAB任意两边之和大于第三边.1955年希腊发行观察这枚邮票上的图案，你有哪些发现?【观察思考】ACB以AB为边的正方形的面积?可以用补的方法设每个小正方形方格的面积都是

1。可以用分割的方法ACB任何直角三角形，以它的两条直角边为一边向三角形外部作的两个正方形的面积之和，等于以斜边为一边向外部作的正方形的面积.【大胆猜想】在所给的方格纸上，任意画一个顶点都在格点上的直角三角

形,分别以各边为边向三角形外作正方形,验证你的猜想！【实验验证】123acbS1+S2=S3猜想:两直角边a、b与斜边c之间的关系？a2+b2=c2【提炼归纳】勾股定理直角三角形两直角边的平方和等于斜边的平方.a2+b2=c2.abcAB

C【得出结论】在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.勾股勾股弦我国是最早了解勾股定理的国家之一。

早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中。商高《周髀算经》勾股定理又称“商高定理”

两千多年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票。毕达哥拉斯毕达哥拉斯定理在Rt△ABC中,∠C=90°(1)已知a=3,b=4,求c;(2

)已知a=6,c=10,求b;(2)在Rt△ABC中,∠C=90°∴a²+b²=c²，又a=6,c=10,∴b²=c²－a²=102－62=64∵b>0，∴b=8ABCacb解:(1)在Rt△ABC中,∠C=90°∴a²+b²=c²，又∵a=3,b=4∴c²=a²+b²=32+4

2=25∵c>0，∴c=5【试一试】方法小结:(1)在直角三角形中,已知两边,可求第三边;(2)可用勾股定理建立方程.（拓展）已知a:b=3:4,c=15,求a、b.7解:∵a²+b²=c²，∴c²=a²+b²=32+42=25在直角△ABC中，

∠B=90°，a=3，b=4，求c2;小明在学习了勾股定理后，很快解决了下面两个问题，并自我感觉良好.请你看看他做得是否正确？【辨一辨】acbACB正解:在Rt△ABC中,∠B=90°∴a²+c²=b²，∴c²=b²-a²=42-32=7求下列直角三角形中未知边的长:12x817②①2

0xx165③【练习1】x=13x=15x=12求下列图中未知数x、y、z的值.【练习2】x=15y=5z=78m6m如图，学校有一块长方形花圃，有少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”，若在拐角的两边缘走，要分别走6米和8米，那么请同学们计算走“捷径”

仅仅少走了几步路,而踩伤了花草.（假设1米为2步）芳草青青，足下留情!【身边的数学】如图,正方形ABCD,你能用今天所学知识画两个个正方形，使它们面积之和等于正方形ABCD的面积吗？画一画.ADCB①②③④⑥⑤E【美丽的数学

】1.已知正方形ABCD的面积是100,s2的面积是64,则DE=_____;2.已知S2=144，S4=16,S3=9,则正方形ABCD面积=________.6169通过本堂课的学习，谈谈你的收获和体会.【学会反思】【课堂小结】观察、

猜想、归纳、验证1.知识点:勾股定理直角三角形两直角边的平方和等于斜边的平方.(揭示了数形结合思想）2.思想方法:体验到定理的一般探究方法利用割补法求图形面积转化（化归思想)通过借助模型进行探究数学建模思想经历探究过程数形

结合，特殊到一般的数学思想《课课练》配套练习部分题选做【作业布置】如果△ABC是锐角三角形、钝角三角形，那么与之间有怎样的大小关系呢？如图①，若△ABC是直角三角形，∠C=90°,那么：222cba22ba2c图①通过今天的学习，我们已经知道：【课后思考】问题1：你能想一个可行的办

法测量出教室的大概高度吗?提供的工具：一根足够长的竹竿；一把皮尺.【身边的数学】问题2:（以教室中一面竖直的墙为例）如图：一根长4.1米的竹竿，架在墙上，测得竹竿下端与墙的距离是0.9米，你能得出教室的高度吗？ABC(变式)若竹竿架在墙上的一端下滑了3.

1米,则其下端滑动了多少米?DE4.10.94.10.9