【文档说明】《2.2 轴对称的性质》教学设计3-八年级上册数学苏科版.docx，共(4)页，86.246 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-25885.html

以下为本文档部分文字说明：

课题：探索轴对称的性质【教学目标】•通过操作活动，经历折叠、画图等过程，探索轴对称的性质。2、会画轴对称图形的对称轴、已知点关于给定直线的对称点，增强学生的空间观念。【教学重点】通过操作活动，经历折叠、画图等过程，探索轴对称的性质。【教学难点】确定已知

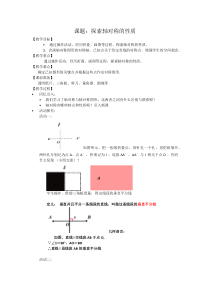
图形的关键点并根据这些点作出对称图形.【课前准备】透明纸片、三角板、剪刀、量角器、圆规等【教学过程】•回忆引入：•我们学习了轴对称与轴对称图形，这两者之间有什么区别与联系呢？•轴对称有哪些特点和性质呢？引入新

课•活动探究：活动一：如图所示，把一张纸折叠后，用针扎一个孔；再把纸展开，两针孔分别记为点A、点A′，折痕记为l；连接AA′，AA′与l相交于点O．你有什么发现（小组交流）？学生操作、借助三角板度量，得出线段的垂直平分线定义：垂直并且平分一条线段的直线，叫做这条线段的垂直平

分线几何语言：如图，直线l交线段AB于点O,∵∠1＝90°，AO＝BO∴直线l是线段AB的垂直平分线活动二：仿照上面的操作，在对折后的纸上再扎一个孔，把纸展开后记这两个针孔为点B、点B′，连接AB、A′B′、B

B′．你有什么新的发现？学生操作、验证、讨论，归纳结论结论：（1）AB=A′B′；（2）直线l垂直平分AA′、BB′；（3）AA′∥BB′活动三：仿照上面的操作，在对折后的纸上再扎一个孔，把纸展开后记这两个针孔为点C、点C′，连接AC、BC、A′C′、B′C′．

你有什么新的发现？你能得出什么结论？（1）⊿ABC≌⊿A′B′C′（2）直线l垂直平分AA′、BB′、CC′（3）AA′∥BB′∥CC′思考：你能总结一下轴对称的性质吗？归纳：轴对称的性质：•成轴对称的两个图形全等•成轴对称的两个图形中，对应点

的连线被对称轴垂直平分．•成轴对称的两个图形中，对应点的连线互相平行或在同一条直线上•性质应用：例1：你能画出四边形ABCD与四边形A′B′C′D′关于某直线对称的对称轴吗？问题（1）：借助透明纸，动手操作，展示，并说出

做法和作图依据问题（2）：不用折叠的方法，利用轴对称的性质，你能画出对称轴吗？（学生作图操作，再通过折叠的方法进行验证，总结作图方法）例2：利用轴对称的性质，你能画出四边形ABCD关于直线l对称的四边形A′B′C′D′吗？思考：（1）怎样画出点D关于直线l的对称点D′呢？说说你的做法

，依据是什么？（2）画出四边形ABCD关于直线l的对称图形需要确定几个点呢？学生操作完成•连接AC、BD，设它们交于点P，怎样找出点P关于直线l的对称点Q，说说你的做法（学生操作，总结作图方法）归纳方法：方法1：折叠打孔找到对称点Q方法2：作点P关于直线

l的对称的点Q方法3：连接A′C′、B′D′，相交于点Q，点Q就是点P关于直线l的对称点方法4：连接A′C′，过点P作直线l的垂线交A′C′于点Q，则点Q即为所求•练习巩固：1、下列说法中，正确的是（）A.关于某直线对称的两个三角形是全等三角形B.全等三角形是关于某直线对称的；C.

两个图形关于某直线对称，则这两个图形一定分别位于这条直线的两侧；D.若A、B关于直线MN对称，则AB垂直平分MN.2、下列说法中错误的是（）A.两个三角形关于某条直线对称，那么这两个三角形全等B.两个图形关于某直线对称，对应点的连线段被对称轴垂直平分C.若直线l同时垂直平分AA

′、BB′，则线段AB=A′B′D.两个图形关于某直线对称，则对应线段相等且平行•小结：通过本节课的学习，你有什么收获？还有哪些疑惑？