【文档说明】中考数学一轮总复习01《实数》知识讲解+巩固练习（基础版）（含答案）.doc，共(13)页，270.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-24885.html

以下为本文档部分文字说明：

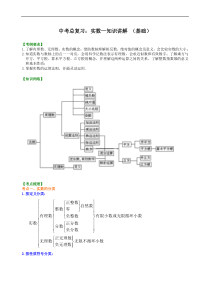
中考总复习：实数—知识讲解（基础）【考纲要求】1.了解有理数、无理数、实数的概念；借助数轴理解相反数、绝对值的概念及意义，会比较实数的大小；2.知道实数与数轴上的点一一对应，会用科学记数法表示有理数，会求近似数和有效数字；了解乘方与开方、平方根、算术平方根、立方根的概念，并理解这两种

运算之间的关系，了解整数指数幂的意义和基本性质；3.掌握实数的运算法则，并能灵活运用.【知识网络】【考点梳理】考点一、实数的分类1.按定义分类：

正整数自然数整数零有理数有限小数或无限循环小数负整数实数正分数分数负分数正无理数无理数无限不循环小数负无理数2.按性质符号分类：正整数正有理数正实数正分数正无理数实数零

负整数负有理数负实数负分数负无理数有理数：整数和分数统称为有理数或者“形如nm（m，n是整数n≠0）”的数叫有理数．无理数：无限不循环小数叫无理数．实数：有理数和无理数统称为实数．要点诠释：常见的无理数有以下几种形式：（1）字母型：如π是无理数，24、等都是无理

数，而不是分数；（2）构造型：如2.10100100010000„（每两个1之间依次多一个0）就是一个无限不循环的小数；（3）根式型：3256、、，„都是一些开方开不尽的数；（4）三角函数型：sin35°、tan27°、cos29°等.考点二、实数的相关概念

1.相反数（1)代数意义：只有符号不同的两个数，我们说其中一个是另一个的相反数．0的相反数是0；（2)几何意义：在数轴上原点的两侧，与原点距离相等的两个点表示的两个数互为相反数；（3)互为相反数的两个数之和等于0.a、b互为相反数a+b=0.2.

绝对值（1)代数意义：正数的绝对值是它本身；负数的绝对值是它的相反数；0的绝对值是0．可用式子表示为：)0()0(0)0(aaaaaa（2)几何意义：一个数a的绝对值就是数轴上表示数a的点

与原点的距离．距离是一个非负数，所以绝对值的几何意义本身就揭示了绝对值的本质，即绝对值是一个非负数．用式子表示：若a是实数，则|a|≥0．要点诠释：若,aa则0a；-,aa则0a；-ab表示的几何意义就是在数轴上表

示数a与数b的点之间的距离.3.倒数（1)实数(0)aa的倒数是a1；0没有倒数；（2)乘积是1的两个数互为倒数．a、b互为倒数1ab.4.平方根（1)如果一个数的平方等于a，这个数就叫做a的平方根．一个正数有两个平方根，它们互为相反数；0有一个平方根

，它是0本身；负数没有平方根．a（a≥0）的平方根记作a．（2)一个正数a的正的平方根，叫做a的算术平方根．a（a≥0）的算术平方根记作a．5.立方根如果x3=a，那么x叫做a的立方根．一个正数有一个正的立方根；一个负数有一个负的立方根；0的立方根仍是0．考点三、实数与数轴规定了原点、正方向和单

位长度的直线叫做数轴，数轴的三要素缺一不可．每一个实数都可以用数轴上的一个点来表示，反过来，数轴上的每一个点都表示一个实数．要点诠释：（1）数轴的三要素：原点、正方向和单位长度.（2）实数和数轴上的点是一一对

应的.考点四、实数大小的比较1.对于数轴上的任意两个点，靠右边的点所表示的数较大.2.正数都大于0，负数都小于0，正数大于一切负数；两个负数；绝对值大的反而小.3.对于实数a、b，若a-b>0a>b；a-b=0a=b；a-b<0a<b.4.对于实数a

，b，c，若a>b，b>c，则a>c.5.无理数的比较大小：利用平方转化为有理数：如果a>b>0，a2>b2a>bba；或利用倒数转化：如比较417与154.要点诠释：实数大小的比较方法：（1

）直接比较法：正数都大于0，负数都小于0，正数大于一切负数；两个负数，绝对值大的反而小.（2）数轴法：在数轴上，右边的数总比左边的数大.考点五、实数的运算1.加法同号两数相加，取相同的符号，并把绝对值相加；绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较

大的绝对值减去较小的绝对值；互为相反数的两个数相加得0；一个数同0相加，仍得这个数．满足运算律：加法的交换律a+b=b+a，加法的结合律(a+b)+c=a+(b+c)．2.减法减去一个数等于加上这个数的相反数．3.乘法两数相乘，同号得正，异号得负

，并把绝对值相乘.几个非零实数相乘，积的符号由负因数的个数决定，当负因数有偶数个时，积为正；当负因数有奇数个时，积为负．几个数相乘，有一个因数为0，积就为0．乘法运算的运算律：（1）乘法交换律ab=ba；（2）乘法结合律(a

b)c=a(bc)；（3）乘法对加法的分配律a(b+c)=ab+ac．4.除法（1）除以一个数，等于乘上这个数的倒数．（2）两个数相除，同号得正，异号得负，并把绝对值相除．0除以任何一个不等于0的数都得0．5.乘方与开方（1)求n个相同因数的积的运算叫做乘方，an所表示的意义

是n个a相乘.正数的任何次幂是正数，负数的偶次幂是正数，负数的奇次幂是负数．（2)正数和0可以开平方，负数不能开平方；正数、负数和0都可以开立方．（3)零指数与负指数011(0)(0).ppaaaaa≠，≠要点诠释

：加和减是一级运算，乘和除是二级运算，乘方和开方是三级运算．这三级运算的顺序是三、二、一．如果有括号，先算括号内的；如果没有括号，同一级运算中要从左至右依次运算．考点六、有效数字和科学记数法一个近似数，四舍五

入到哪一位，就说这个近似数精确到哪一位．一个近似数，从左边第一个不是0的数字起，到精确到的数位为止，所有的数字，都叫做这个近似数的有效数字．精确度的形式有两种：（1）精确到哪一位；（2）保留几个有效数字.把一个数用±a³10n（其中1≤＜10，n为整数

）的形式记数的方法叫科学记数法．要点诠释：（1）当要表示的数的绝对值大于1时，用科学记数法写成a³10n，其中1≤a＜10，n为正整数，其值等于原数中整数部分的数位减去1；（2）当要表示的数的绝对值小于1时，用科学记数法写成a³10n，其中1

≤a＜10，n为负整数，其值等于原数中第一个非零数字前面所用零的个数的相反数（包括小数点前面的零）.【典型例题】类型一、实数的有关概念1．（1）a的相反数是15，则a的倒数是_______．（2）实数a、b在数轴上对应点的位置如图所示

:则化简2()ab＋=______．0ab（3）（泉州市）去年泉州市林业用地面积约为10200000亩，用科学记数法表示为约____________．【答案】（1）5；（2）-a-b；（3）1.02³107亩.【

解析】（1）注意相反数和倒数概念的区别，互为相反数的两个数只有性质符号不同，互为倒数的两个数要改变分子分母的位置；或者利用互为相反数的两个数之和等于0，互为倒数的两个数乘积等于1来计算.（2）此题考查绝对值的几何意义，绝对值和二次根式的化简.注意要去掉绝对值符号，要判别

绝对值内的数的性质符号.由图知：200||||0()||().ababababababab，，，，（3）考查科学记数法的概念.【点评】本大题旨在通过几个简单的填空，让学生加强对实数有关概念的理解．举一反三：【变式】据市旅游局统计，今年“五²

一”小长假期间，我市旅游市场走势良好，假期旅游总收入达到8.55亿元，用科学记数法可以表示为（）A．8.55³106B．8.55³107C．8.55³108D．8.55³109【答案】C.类型二、实数的分类与计算2．下列实数227、sin60°、3、02、3.14159、-9、

27、8中无理数有（）个A．1B．2C．3D．4【答案】C.【解析】无理数有sin60°、3、8.【点评】对实数进行分类不能只看表面形式，应先化简，再根据结果去判断．举一反三：【高清课程名称：实数高清ID号：369214关联的位置名称（播放点名称）：经典

例题1】【变式】在,30cos,2π,)23(,4,8,14.30,45tan,712,1010010001.0,5113.0%,3中，哪些是有理数?哪些是无理数?【答案】03.14,4,(32),,45tan,712,5113.

0%,3都是有理数；π8,,cos30,20.1010010001,都是无理数.3．（2015•梅州）计算：+|2﹣3|﹣（）﹣1﹣（2015+）0．【答案与解析】解：原式=2+3﹣2﹣3﹣1=﹣1．【点评】该题是实数的混合运算，包括绝对值，0指数幂、负整数指数幂等．只要准确把握各自的

意义，就能正确的进行运算．举一反三：【高清课程名称：实数高清ID号：369214关联的位置名称（播放点名称）：经典例题8-9】【变式1】计算：（2015•甘南州）计算：|﹣1|+20120﹣（﹣）﹣1﹣3t

an30°．【答案】解：原式=﹣1+1﹣（﹣3）﹣3×=+3﹣=3．【变式2】计算：12004200320022001【答案】设n=2001，则原式=1)3)(2)(1(nnnn1)23)(3(22nnnn（把n2+3n看作一

个整体）=1)3(2)3(222nnnn=n2+3n+1=n(n+3)+1=2001³2004+1=4010005.类型三、实数大小的比较4．比较下列每组数的大小：（1）417与154（2）a与a1（a≠0）【答案与解析】（1）11740174，14150415

，而174与415可以很容易进行比较得到：1744150，所以174415；（2）当a<-1或O<a<1时，a<a1；当-1<a<0或a>1时，a>a1；当a=1时，a=a1.【点评】（1）有时无理数比较大小，通过平方转化以后也无法进行比较

，那么我们可以利用倒数关系比较；（2）这道题实际上是互为倒数的两个数之间的比较大小，我们可以利用数轴进行比较，我们知道，0没有倒数，±1的倒数等于它本身，这样数轴就被这3个数分成了4部分，下面就可以分类讨论每种情况.我们还可以

利用函数图象来解决这个问题，把a1的值看成是关于a的反比例函数，把a的值看成是关于a的正比例函数，在坐标系中画出它们的图象，可以很直观的比较出它们的大小.举一反三：【变式】比较下列每组数的大小：（1）817和511（2）52和2

3【答案】（1）将其通分，转化成同分母分数比较大小，1785840，1188540，171185，所以171185.（2）2257210740，232743748，因为4048，所以2532.类型四、平方根的应用5．已知：x，y是实

数，234690xyy，若axy-3x=y，则实数a的值是_______.【答案】14.【解析】234690xyy，即234(3)0xy两个非负数相加和为0，则这两个非负数必定同时为0，∴340x，(y-3)2=0，∴x=43，y=3又∵axy-3x=y，∴a=

43()33134433xyxy.【点评】此题考查的是非负数的性质.类型五、实数运算中的规律探索6．细心观察图形，认真分析各式，然后解答问题2122231112,22213,23

314,2SSSS1S2S3S4S5OA1A2A3A4A5A611111（1）请用含有n（n是正整数）的等式表示上述变化规律；（2）推算出OA10的长；（3）求出S12+S22+S32+„

+S102的值.【答案与解析】（1）由题意可知，图形满足勾股定理，2,112nSnnn（2）因为OA1=1，OA2=2，OA3=3„，所以OA10=10（3）S12+S22+S32+„+S

102=2222)210()23()22()21(=)10321(41=455.【点评】近几年各地的中考题中越来越多的出现了一类探究问题规律的题目，这些问题素材的选择、文字的表述、题型的设计不仅考察了数学的基础知识，基本技能，更重点考察了创新意识和能力，还考察了认真观

察、分析、归纳、由特殊到一般，由具体到抽象的能力.举一反三：【变式】图中是一幅“苹果图”，第一行有1个苹果，第二行有2个，第三行有4个，•第四行有8个，„„你是否发现苹果的排列规律？猜猜看，第十行有______个苹果．【答案】29（512）.

中考总复习：实数—巩固练习（基础）【巩固练习】一、选择题1.在实数－23，0，3，－3.1415，2，9，－0.1010010001„（每两个1之间依次多1个0），sin30°这8个实数中，无理数有（）A．1个B．2个C．3个D．4个2．我

国第六次全国人口普查数据显示，居住在城镇的人口总数达到665575306人．将665575306用科学记数法表示（保留三个有效数字）约为（）A．66.6³107B．6.66³108C．0.666³10

8D．6.66³1073．（2015•杭州）若k＜＜k+1（k是整数），则k=（）A．6B．7C．8D．94．在三个数0.5、、中，最大的数是()A．0.5B．C．D．不能确定5．用四舍五入法按要求对0.05049分别取近似值，其中错误的

是（）A．0.1（精确到0.1）B．0.05（精确到百分位）C．0.050（精确到0.001）D．0.05（精确到千分位）6．我国古代的“河图”是由3³3的方格构成，每个方格内均有数目不同的点图，每一行、每一列以及每一条对角线上的三个

点图的点数之和均相等．图中给出了“河图”的部分点图，请你推算出P处所对应的点图是()二、填空题7．0201112yx则xy=.8．（2014•辽阳）5﹣的小数部分是．9．若22ba与互为相反数，则a+b的值为___

_____．10．已知a与b互为相反数，c与d互为倒数，m的绝对值是1，则2mcdmba的值为________．11．已知：22222233445522334455338815152424，，，

，，若21010bbaa符合前面式子的规律，则a+b=________．12．将正偶数按下表排列：第1列第2列第3列第4列第1行2第2行46第3行81012第4行14161820„„根据上面的规律，则2006所在行、列分别是________．三、解答题13．计算

：（1）2012201280.125（2）222121eeee14．若333)43(,)43(,)43(cba，比较a、b、c的大小。15．在数学活动中，小明为了

求2341111122222n的值（结果用n表示），设计如图（1）所示的几何图形．（1）请你利用这个几何图形求2341111122222n的值为_______．（2）请你利用图（2）再设计一个能求2341111122222n的值的几何图形

．16.（2014春•双流县月考）求（2+1）（22+1）（24+1）„（232+1）+1的个位数字．【答案与解析】一、选择题1.【答案】C；【解析】对实数分类，不能只为表面形式迷惑，而应从最后结果去判断．首先明确无理数的概念，即“无限不循环小数叫做无理数”.一般

来说，用根号表示的数不一定就是无理数，如93是有理数，关键在于这个形式上带根号的数的最终结果是不是无限不循环小数．同样，用三角符号表示的数也不一定就是无理数，如sin30°、tan45°等．而－0.1010010001„尽管有规律，•但它是无限不

循环小数，是无理数．2是无理数，而不是分数．在上面所给的实数中，只有3，2，－0.1010010001„这三个数是无理数，其他五个数都是有理数，故选C.2.【答案】B；【解析】科学记数法的表示形式为a³10n的形式，其中1≤|a|＜10，n为整数．确定n的值是关键点，

由于665575306有9位，所以可以确定n=9﹣1=8.有效数字的计算方法是：从左边第一个不是0的数字起，后面所有的数字都是有效数字，故选B．3.【答案】D.【解析】∵k＜＜k+1（k是整数），9＜＜10，∴k=9．故选：D．4.【答案】B；5.【答案】D；【解析】根据近似数与有效

数字的概念对四个选项进行逐一分析即可：A、0.05049精确到0.1应保留一个有效数字，是0.1，故本选项正确；B、0.05049精确到百分位应保留一个有效数字，是0.05，故本选项正确；C、0.0504

9精确到0.001应是0、050，故本选项正确；D、0.05049精确到千分位应是0.050，故本选项错误.故选D.6.【答案】C；【解析】设左下角小方格内的点数为x（如图），则依题意得2+5+x=x+1+

p,解得p=6.二、填空题7．【答案】－1；【解析】根据非负数的性质，要使0201112yx，必须1020110xy，即12011xy.因此201111yx.8．【答案】2﹣；【解析】由1＜＜2，得﹣2＜﹣＜﹣1．不等式的两边都加5

，得5﹣2＜5﹣＜5﹣1，即3＜5﹣＜4，5﹣的小数部分是（5﹣）﹣3=2﹣，故答案为：2﹣．9．【答案】0；【解析】由绝对值非负特性，可知02,02ba，又由题意可知：022ba所以只

能是：a–2=0，b+2=0，即a=2，b=–2，所以a+b=0.10．【答案】0；【解析】原式=0110.11．【答案】109；【解析】规律22211nnnnnn，所以a=99，b=10，a+b=109.1

2．【答案】第45行第13列【解析】观察数列2，4，6，8，10，...每个比前一个增大2，2006是这列数字第1003个.每行数字的个数按照1，2，3，4，5，...，n递增，根据等差数列求和公式，第n行（包括n行）以前的所有数字的个数(1)2nn.如果20

06在第n行，那么10032)1(nn设10032)1(nn,解得n约为44.5，n取整数，因此n=45。到第44行（含44行）共有数字（44+1）³244=990个；到第45行（含45行）共有数字（45+1）³245=1035个；2006是第1003

个，在45行13列.三、解答题13.【答案与解析】（1）原式=20122012(80.125)11（2）原式=21212121eeeeeeee=11ee14.【答案与解析】34()3a＜-1；334b

＞-1且＜0；c＞0；所以容易得出：a＜b＜c.15.【答案与解析】（1）112n(2)16.【答案与解析】解：原式=（22﹣1）（22+1）（24+1）（28+1）„（232+1）+1=（24﹣1）（24+1）（28+1）„（232+1）+1=264﹣1+1=

264；∵21=2，22=4，23=8，24=16，25=32，„∴2的整数次幂的个位数字每4个数字为一个循环组依次循环，∵64=16³4，∴264的个位数字与24的个位数字相同，为6，∴原式的个位数字为6．