【文档说明】《回顾与反思》教学设计1-九年级下册数学冀教版.docx，共(4)页，432.764 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-23031.html

以下为本文档部分文字说明：

1课题圆中的分类讨论课型复习课教法五步教学法教具多媒体教学目标1.。2.能够利用勾股定理解决一些简单的实际问题教学重点难点重点：勾股定理的验证和应用难点：勾股定理的验证教学过程教学设计学生活动一、点和圆产生的分类

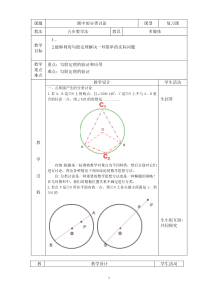
讨论1.若A、B是⊙O上的两点，且∠AOB=1400，C是⊙O上不与A、B重合的任意一点，则∠ACB的度数是_________.归纳:根据某一标准将数学对象分为不同种类，然后分别对它们进行讨论，得出各种情况下相应结论的数学思想方法。注:分类讨论是一种重要的数学思想

方法也是一种解题的策略！在几何图形中，我们常根据位置关系不确定进行分类。2.若点P是⊙O所在平面内的一点，到⊙O上各点最小距离是1，到⊙O的生回答生小组互助，共同探究教教学设计学生活动2学过程最大距离是7，该圆的半径为___________反思:点与圆的位

置关系不确定.二、线与圆产生的分类讨论。3．已知横截面直径为100cm的圆形下水道，如果水面宽AB为80cm，则下水道中水的最大深度.反思：弦与圆心的位置关系不确定产生分类讨论4．如图，已知在直角坐标系中，

半径为2的圆的圆心坐标为（3，-3），当该圆向上平移______个单位时，它与x轴相切.反思：切线与圆心的位置关系不确定产生分类讨论。5．如图，点P为正比例函数图象上的一个动点，⊙P的半径为3，设点P的坐标为．求⊙P与直线相切时点的坐标．生独立思考，

画图求解生思考解决36．直线334yx与x轴，y轴分别交于点M，N，（1）求M，N两点的坐标；（2）如果点P在x轴上，以点P为圆心，3为半径的圆与直线334yx相切，求点P的坐标.三、小结1．

归纳小结：点、弦、直线与圆位置不确定需分类讨论2．圆是轴对称图形3．分类思想在动态问题中运用四、作业布置：名校课堂相应内容。学生画图求解学生讨论解决4教学反思1.点与圆有三种位置关系，位置关系的不确定产生

了分类讨论；2.线与圆有三种位置关系，位置关系的不确定产生了分类讨论。3.圆是轴对称图形，圆自身的轴对性也易产生分类。