【文档说明】《小结练习（2）》PPT课件9-九年级下册数学湘教版.ppt，共(16)页，708.500 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-19632.html

以下为本文档部分文字说明：

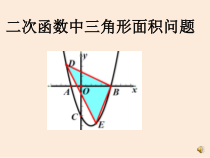
二次函数中三角形面积问题复习回顾三角形的面积是怎么求的？二次函数中三角形面积问题该怎么解决呢？如图所示，抛物线y=x2-4x-5与x轴相交于点A和点B，与y轴交于点C.课前热身:（-1,0）（0,-5）问1：能求出点A、B、C的坐标吗？（5

,0）如图所示，抛物线y=x2-4x-5与x轴相交于点A和点B，与y轴交于点C.探究活动一:问2：连接AC、BC,则S△ABC是多少？（-1,0）（0,-5）（5,0）如图所示，抛物线y=x2-4x-5与x轴相交于点A和点B，与y轴交于点C.探究活

动一:变1：若AB不动,D（2，-9），则S△ABD=______.27变2：若AB不动,D（6，7），则S△ABD=______.21（-1,0）（5,0）(2,-9)E（-1,0）（5,0）(6,7)E探究活动一:变3：若AB不动,D（x，y）为抛物线任意一点，则S△ABD=____

_____.直接求面积法(x，y)(-1,0)(5,0)E(5,0)(x，y)E(-1,0)3y(2,-9)(0,-5)(5,0)(-1,0)探究活动二:变4：若BC不动，点D(2,-9)，则S△BCD=________.大显身手割补法y=x2-4x-5探究活动三:变5：若BC不动，

点D为线段BC下方抛物线上一动点，则S△BCD是否存在最大值，若存在，求此时点D的坐标；若不存在，请说明理由.(-1,0)(0,-5)(5,0)小组交流小组展示y=x2-4x-5探究活动三:变5：若BC不动，点D为线段BC下方抛物线上任意一动点，则S△BCD是否存在

最大值，若存在，求此时点D的坐标；若不存在，请说明理由.F12DEOB52DEE(-1,0)(5,0)S△BCD=S△CED+S△BDE12DECM12DEBF1()2DECMBF1()2DEOFBFM(0,-5)y=x2-4x-5探究活动三:FS△BCD=12DEOB

52DEE(-1,0)(5,0)(m,m2-4m-5)(m,)直线BC:y=x-5m-5DE=yE-yD=-m2+5mS△BCD=25(5)2mm25125285()2m当时，ΔBCD面积有最大值为.52m1258535(,)24D此

时.=(m-5)-(m2-4m-5)(0,-5)MS△BCD=S△CED+S△BDE12OBDE解题反思（5,0）（0,-5）（x,y）EF12S水平宽x铅垂高铅垂高水平宽D(x右-x左)(y上-y下)12S水平宽x铅垂高(y上-y下)(x右-x左)12如图，抛物线y

=-x2-2x+8与直线AB相交于A（1，5），B（-5，-7）.牛刀小试:（1）求直线AB的表达式;（2）点P为直线AB上方抛物线一动点,则△ABP的面积是否有最大值，若有请求出来，若不存在，请说明理由．(y上-y下)(x右-x左)12S

解：(1)y=2x+3;(2)当P(-2,-1)时，ΔABP面积有最大值为27.函数图像中的面积计算要跟点的坐标联系起来，学会转换线段与点的坐标之间的关系.求三角形面积，关键就是要找到底与高，实在不行可以构造底或高.要注意点的坐标

与线段长之间的区别，坐标有正负，线段长都是正的.(y上-y下)(x右-x左)12S当堂测评已知抛物线y=-x2+2x+3交x轴于点A和B，交y轴于点C,顶点坐标为D.（1）求S△BCD(2)设点E是线段BC上方的抛物线上的一个动点，是否存在一点

E，使S△EBC面积最大？若存在，请求出点E的坐标，若不存在，请说明理由.22(1)3;39(2)2232728315(,)243()2yPxx