【文档说明】《2.1多边形的概念及内角和》导学案-八年级下册数学湘教版.doc，共(3)页，96.500 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-19386.html

以下为本文档部分文字说明：

课题探索多边形的内角和课时第一课时课型讲、议、练相结合学习目标1、掌握多边形内角和定理，进一步了解转化的数学思想。2、经历质疑、猜想、归纳等活动发展学生的合情推理能力，积累数学活动的经验，在探索中学会与人合作，学会交流自己的思想和方法。学

习重点多边形内角和定理的探索和应用。学习难点多边形定义的理解；多边形内角和公式的推导；转化的数学思维方法的渗透。实施过程教师活动学生活动一、自学检测，概念学习1、在平面内，由一些线段首尾顺次相接组成的封闭图形叫作。2、相邻两边组成的

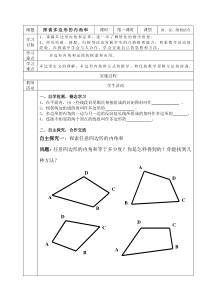
角叫作多边形的。3、多边形的内角的一边与另一边的反向延长线所组成的角叫作多边形的。4、连接不相邻的两个顶点的线段叫作多边形的。二、自主探究，合作交流自主探究一：探索任意四边形的内角和问题：任意四边形的内角和等于多少度？你是怎样得到的？你能找到几种

方法？ACBAABBCCCDDDBDA自主探究二：探索多边形的内角和公式问题：选择同一种方法分别求出任意五边形、六边形、七边形的内角和等于多少度？结论：n边形的内角和等于。三、实践应用：例：十边形的内角和是多少度数？四、课

堂练习，运用新知1、巩固练习：（1）一个多边形的内角和等于1980°，它是几边形？（2）正十二边形的内角和是多少？每一个内角是多少度2、求下列图形中x的值：A11A2A3A4A5An五边形六边形七边形AAABBBCCCDDDEEEFFG0x0x01200800x07501401360五、拓展

延伸：1、欣赏多边形平铺图片2、动手拼一拼请同学们拿出准备好的正多边形纸片，小组合作，用同一种图形依次拼凑，观察有哪几种情形可以拼出平整、无空隙的图案？哪几种不可以？为什么？六、课堂小结：1.本节课，你有何收获？2.

你还有什么疑惑？七、课后作业：1、在2008年的北京奥运会上有很多设计美丽的多边形花坛,猜想:是否存在一个内角和为2008°的花坛?2、一天小明爸爸给小明出了一道智力题考考他。将一个多边形截去一个角后(没有过顶点）得到多边形的内角和将会（）A、不变B、增加180°C、减少

180°D、无法确定教与学反思