【文档说明】《4.5 相似三角形的性质及应用》PPT课件1-九年级上册数学浙教版.ppt，共(17)页，1.151 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-18738.html

以下为本文档部分文字说明：

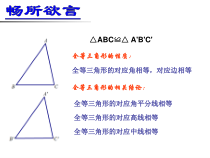
全等三角形的对应角相等，对应边相等全等三角形的性质：全等三角形的相关结论：全等三角形的对应角平分线相等全等三角形的对应高线相等全等三角形的对应中线相等△ABC≌△A'B'C'全等三角形的对应角相等，对应边相等相似三角形的对应角相等，对应边成比例全等三角形

的性质：相似三角形的性质：全等三角形的相关结论：相似三角形的相关结论：全等三角形的对应角平分线相等相似三角形的对应高线之比等于相似比相似三角形的对应角平分线之比等于相似比相似三角形的对应中线之比等于相似比全等三角形的对应高线相等全等三角形的对应中线相等类比猜想△ABC≌△A'B

'C'△ABC∽△A'B'C'1、如图，已知△ABC∽△A’B’C’，相似比为，AD与A’D’为这两个三角形的角平分线，求AD与A’D’的比kC'B'BC笛卡尔说过:我所解决的每一个问题都将成为一个范例,以用于

解决其他问题,这便是学习数学的真谛!1、如图，已知△ABC∽△A’B’C’，相似比为，AD与A’D’为这两个三角形的角平分线，求AD与A’D’的比将AD与A’D’改为高线，求AD与A’D’的比kC'B'BC变式1：如图，已知△ABC∽△A’B

’C’，相似比为，AD与A’D’为这两个三角形的高线，则kkC'B'BC''DAADk变式2：如图，已知△ABC∽△A’B’C’，相似比为，AD与A’D’为这两个三角形的中线，则''DAADkC'B'BC全等三角形的对应角相等，对应边相等相似

三角形的对应角相等，对应边成比例全等三角形的性质：相似三角形的性质：全等三角形的相关结论：相似三角形的相关结论：全等三角形的对应角平分线相等相似三角形的对应高线之比等于相似比相似三角形的对应角平分线之比等于相似比相似三角形的

对应中线之比等于相似比全等三角形的对应高线相等全等三角形的对应中线相等类比猜想△ABC≌△A'B'C'△ABC∽△A'B'C'验证PE2、如图，已知AD，CE是△ABC的两条中线，P是它们的交点，证明：CP

EPAPDPFkC'B'BC变式2：如图，已知△ABC∽△A’B’C’，相似比为，AD与A’D’为这两个三角形的中线，则''DAADk如图，已知AD，BF是△ABC的两条中线，Q是它们的交点，则AQDQ2

1APDP211、如图，AD为△ABC的一条中线，P为△ABC的重心，连结BP，若,则2BDPSABCS12S2S3SSSSSSS1:21:22、如图，在△ABC中，中线AD，BF相交于点P，过点F作EF∥BC，交AD于点E，则AE:AD=，

EP:PD=AE:EP=?3:1我们有哪些收获？---与大家共分享！学而不思则罔回头一看，我想说…小结学而不思则罔回头一看，我想说…三角形若相似对应角则相等对应边成比例中线高线角平分线对应也是成比例比值都是相似比线段比我能行相似三角形找一找

三中线交一点此点称之为重心它分中线1:2有一块三角形的余料ABC，它的边BC=120，高AD=80，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上，则加工成的正方形零件的边长为BCFIADAE1208080aa△AFI∽△ABC48a80-aa