【文档说明】《阅读材料 从勾股定理到图形面积关系的拓展》教学设计1-八年级上册数学浙教版.doc，共(5)页，337.000 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-18437.html

以下为本文档部分文字说明：

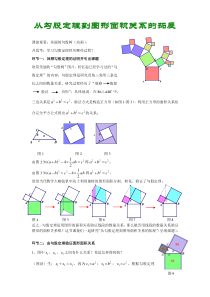
CDBAFABCABCBACABCBACcbaABC课前观看：美丽的勾股树（动画），并思考：学习勾股定理经历哪些过程？环节一：回顾勾股定理的证明并引出课题欣赏美丽的“勾股树”图片，回忆起已经学习过的“勾股定理”的内容：勾股定理是研究直角三角形三条边长之间的

数量关系，研究过程经历了“观察猜想验证应用”；具体地说，在Rt△ABC中，三边关系是222abc，验证方式是构造正方形（如图1-图3），利用正方形的面积关系结合完全平方公式得出222abc的关系；图1图2图3由图2知221()42ababc得222abc；由

图3知221()42abcab得222abc。欣赏当代数学大咖张景中院士利用独特的图形面积分割、转化，验证了勾股定理：图4图5图6图7图8总之，勾股定理是用图形的面积关系验证线段的数量关系，那么能否用线段的数量关系验证

图形的面积关系呢？这节课我们一起研究“从勾股定理到图形面积关系的拓展”（呈现课题）。环节二：由勾股定理验证图形面积关系1、图中1s，2s，3s之间有什么关系？你是怎样得到的？（预设）生：123sss，因为1s=2a；2s=2b；3s=2c，根据勾股定理从勾股定理到图形面积关系的拓展

baccba图9S3S2S1ABCS1S2S3BAC222abc得123sss。结论：以直角三角形的三边为边长向外作正方形，得到的两个小正方形面积之和等于大正方形的面积。我们把这个结论记作123sss。2、

除了向外作三个正方形外还可以向外作哪些几何图形？结论还成立吗？（等边三角形，半圆，等腰直角三角形等，根据学生描述的顺序点击相应的图形）图10图11图12图13图143、在师生作图基础上逐个解释图形的面积关系，如图10往外作等边

三角形113s22aa234a，同理223s4b，233s4c，根据222abc得123sss。重点解释等腰直角三角形（图11、12）的面积关系，从代数列式、几何图形两个方面解释。4、将图12等腰直角三角形改为一般的

等腰三角形（图15），上述结论123sss还成立吗？如果不成立，需要添加什么条件才能使得123sss成立？图13中向外作长方形呢？（教师引导学生计算相应的高线与a，b，c比值高线）发现结论，揭示本质：以直角三角形的三边为底边向外作等腰三角形，

三个图形的对应高线与底边之比的比值保持相等，则结论123sss都成立。5、更一般地，改变图15中高线的位置得到一般的三角形，结论仍成立。环节三：拓展应用，翻折变换1、将图14中半圆3s沿AB翻折得月牙图（图16），图中1s，2s，3s之间有什

么关系？你是怎样得到的？（学生思考、回答，师生补充完善）cbaS3S2S1BACP图15图16若ABC=30°S1S2S3EDNMGFABCcbaS3S4S1S2ABCS2S1S3S4EFBAC2．类似的，将图9中3s沿AB翻折得图17，则图中1s，2s，3s，4s之间有什么关系？你是怎样得

到的？（讨论交流汇报）1342+=+sssss4=ss132==ssss环节四：知识运用练习1.如图，已知在Rt△ABC中，∠ACB=Rt∠，AB=4，分别以AC、BC为直径作半圆，面积分别记为S1、S2，则S1+S

2的值等于.变式1：图19中添加∠ABC=30°，则月牙S1+S2的值等于.练习2.如图，在Rt△ABC中，∠C=90°，分别以AB、AC、BC为边，在AB的同侧作正方形ABEF、ACPQ、BDMC，四块阴影部分的面积分别为S1、S2、S3、

S4，若S正方形ABEF=25，S正方形ACPQ=9，则S1+S2+S3+S4等于（）A.12B.15C.18D.20练习3.如图，在△ABC中，∠ACB＝90º，AC＞BC，分别以AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG，连

接EF、GM、ND，设△AEF、△BND、△CGM的面积分别为S1、S2、S3，则下列结论正确的是（）A．S1＝S2＝S3B．S1＝S2＜S3C．S1＝S3＜S2D．S2＝S3＜S1图17图18图19BAC练习4.已知：如图，以Rt△ABC的三边a、b、c为边分别向外作等腰

直角三角形．面积分别为S1、S2、S3，若斜边c＝6，则S1+S2为．环节五：课堂小结知识：从勾股定理到图形面积关系的拓展能力：转化、应用、创新思想方法：类比、建模、化归、特殊到一般、分类讨论类比分类

讨论特殊到一般从勾股定理到图形面积关系的拓展cabS3S2S1BACcabS3S2S1BACcabS1S2S3ABCcabS3S2S1BACcabS1S2S3ABCPS3S2S1ABC板书设计：观察——猜想——验证——应用类比转化222abc

本质：三个图形对应高线与边长之比的比值保持相等，则结论123sss都成立。