【文档说明】《复习题》导学案1-八年级上册数学华师大版.doc，共(1)页，57.000 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-14067.html

以下为本文档部分文字说明：

《全等三角形复习习题课1——对SSA的探究》学案一、课前完成.㈠全等三角形判定方法有：SAS、、、和，要特别注意“两边和分别对应相等的两个三角形()”不一定全等。请思考：SSA在什么情况下成立?在什么情况下不成立?㈡思考：满足:“两边和一角分别对

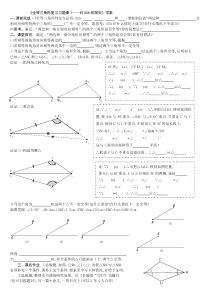
应相等”的两个三角形是否全等?你有何想法?二、课堂探究.满足:“两边和一角分别对应相等”的两个三角形是否全等?你有何想法?㈠若相等的角为对应相等两边的,则这两个三角形全等,根据㈡若相等的角为对应相等两边其中一边的,则这两个三角形不一定全等.⒈当这个角为时这两个三角形全等,根据

；⒉当这个角为时这两个三角形全等,证明如下.已知：△ABC和△A1B1C1,∠A=∠A1>90°,AB=A1B1,BC=B1C1,求证：△ABC≌△A1B1C1.证法一:把钝角△转化为证法二:重合法证法三:构造等腰△⒊当这个角为时这两个△不一定全等!是什么原因?在什么情况下一定

全等?画图发现:∠A=30°,AB=4cm,⑴BC=1.5cm;⑵BC=2cm;⑶3cm;⑷BC=4cm;⑸BC=5cm.原因:当时,符合条件的△只能画出1个,两个△全等.三、课后作业.⒈必做题.如图,已知:∠1=∠2,为使△ABC≌△ABD,必须补充一个条件,请补上这个条件.要求至少写6种情

况,并给予证明.⒉选做题.整理本节课的研究成果，以《有趣的“SSA”》为题目(也可自拟题目),写一篇小论文,一周后交上(可以2至4人合作).4321ABCDC1B1A1CBAC1B1A1CBAC1B1A1CBA证:作()⊥()

于D,()⊥()于D1,∴∠=∠=90°,∵∠=∠∴∠=∠∵()=(),∴△≌△,∴()=(),∵()=(),∴△≌△,∴∠=∠,∴△≌△.证:∵()=(),∴可把△A1B1C1移到如图位置,使B1C1与BC重合,A与A1分别在BC的两侧,连结∵()=(),∴∠=∠

∵∠=∠,∴∠=∠,∴()=(),∵()=(),∴△≌△.证:∵∠=∠,()=()∴可把△A1B1C1移到如图位置,使A1B1与AB重合,∠BAC与∠N1A1C1重合.只要证C与C1重合.假设C与C1不重合,不妨设C1在AC的延长线上,∵BC=B1C1，∴∠C1=

∠>∠BAC>>90°∴∠+∠+∠>()°这与三角形内角和等于矛盾！∴假设C与C1不重合是错误的，∴△≌△.⑴BA⑵⑶⑷BAABAB⑸AB