【文档说明】《积的乘方》PPT课件1-八年级上册数学华师大版.ppt，共(25)页，901.500 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-14018.html

以下为本文档部分文字说明：

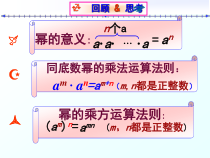
回顾与思考回顾&思考☞幂的意义:a·a·…·an个aan=同底数幂的乘法运算法则：am·an=am+n（m,n都是正整数）幂的乘方运算法则:(am)n=(m、n都是正整数)amnam·an同底数幂相

乘（am)n幂的乘方（ab)3积的乘方——积的乘方12.1幂的运算（3）探索与交流(1)根据乘方定义(幂的意义)，(ab)3表示什么?探索&交流参与活动：(2)为了计算(化简)算式ab·ab·ab，可以应用乘法的交换律和结合律。又可以把它写成什么形式?探索与交流探索&交流参与活动：(a

b)3=ab·ab·ab=a·a·a·b·b·b=a3·b3(3)由特殊的(ab)3=a3b3出发，你能想到一般的公式吗?猜想(ab)n=anbn的证明在下面推导中说明每一步变形的依据：(ab)n=ab·ab·……·ab()=(a·a·……·a)(b

·b·……·b)=an·bn．()幂的意义(乘法交换律、结合律)幂的意义n个abn个an个b♐(ab)n=an·bn积的乘方法则上式显示:积的乘方=.(ab)n=an·bn积的乘方乘方的积（n是正整数）每个因式分别乘方后的积积的乘方法则积的乘方法则积的乘方法则你能说出法则中“因式”这两个

字的意义吗?(a+b)n，可以用积的乘方法则计算吗?即(a+b)n=an·bn成立吗？又(a+b)n=an+bn成立吗？公式的拓展三个或三个以上的积的乘方，是否也具有上面的性质?怎样用公式表示?(abc)n=an·bn·cn怎样证明?(abc)n=[(ab)·c]n=(ab)n·cn=an·b

n·cn.例题解析【例1】计算：(1)(2b)3;(2)(-a)3;(3)(-3x)4;(4)(2a3)2.=23b3=8b3;(1)(2b)3解：(2)(-a)3=(-1)3a3=-a3;(3)(-3x)4=(-3)4x4=81x4(4)(2a

3)2=22(a3)2=4a6阅读体验☞1.判断下列计算是否正确，并说明理由：=xy6(2)(-2x)3=-6x3（1）(xy3)2巩固练习2计算：(1)(3a)2;(2)(-3a)3;(3)(ab3)2(4)(-2×103)3=32a2=9a2;(1)(3a)2解：(2

)(-3a)3=(-3)3a3=-27a3;(3)(ab3)2=a2(b3)2=a2b6(4)(-2×103)3=-8×109例题解析【例2】地球可以近似地看做是球体，如果用V,r分别代表球的体积和半径，那么。地球的半径约为6×103千米，它的体积大约是多少立方千米?阅读体验☞334rV例题

解析解：阅读体验☞334rV34=×(6×103)334=×63×109≈9.04×1011(千米3)注意运算顺序!公式的反向使用(ab)n=an·bn（n是正整数）反向使用:an·bn=(ab)n公式的反向使用试用简便方法计算:

(1)23×53;(2)28×58;(3)(-5)16×(-2)15(4)24×44×(-0.125)4=(2×5)3=103=(2×5)8=108=(-5)×[(-5)×(-2)]15=[2×4×(-0.125)]4=1.=-5×1015练习3、

计算：72708)125.0)(1(23)()()2(nmyxyx本节课你的收获是什么？幂的意义:a·a·…·an个aan=同底数幂的乘法运算法则：am·an=am+n积的乘方运算法则:(ab)n=anbn积的乘方=.反向使用am·an=am+n、(am)

n=amn可使某些计算简捷。每个因式分别乘方后的积公式的拓展三个或三个以上的积的乘方，是否也具有上面的性质?怎样用公式表示?有两种思路______一种思路是利用乘法结合律，把三个因式积的乘方转化成两个因式积的乘方、再用积的乘方法则;另一种思路是仍用推

导两个因式的积的乘方的方法：乘方的意义、乘法的交换律与结合律.方法提示3、计算：的值求已知nmnm232,42,32)3(例题解析【例2】计算：(1)(3x)2;(2)(-2b)5;(3)(-2xy)4;(4)(3a2)n.=32x2=9x2;(1)(3x)2

解：(2)(-2b)5=(-2)5b5=-32b25;(3)(-2xy)4=(-2x)4y4=(-2)4x4y4(4)(3a2)n=3n(a2)n=3na2n。阅读体验☞=16x4y4；3、计算：的值求已知2685152

0,64)3(zyxzyx的值求已知nmnm232,42,32)4(随堂练习随堂练习p181、计算：(1)(-3n)3;(2)(2)(5xy)3;(3)(3)–a3+(–4a)2a。三、过手训练：1.计算：224)3)(1(yx43)()2(nm21

3)())(3(mmaann则如果,3)9()1(82baba236,27)2(则2.填空：