【文档说明】《14.2 勾股定理的应用》PPT课件1-八年级上册数学华师大版.ppt，共(20)页，2.306 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-14012.html

以下为本文档部分文字说明：

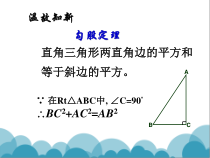
温故知新勾股定理直角三角形两直角边的平方和等于斜边的平方。ABC∵在Rt△ABC中,∠C=90ºBC2+AC2=AB2如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.abc勾股定理的逆定理∵

a2+b2=c2∴ΔABC为直角三角形如图，学校有一块长方形花园，有极少数人为了避开拐角走“捷径”，在花园内走出了一条“路”，仅仅少走了________步路,却踩伤了花草。（假设1米为2步）3米4米“路”ABC5

米4问题情境：☞学习目标1.能运用勾股定理及其逆定理解决简单的实际问题.(重点)2.经历勾股定理的应用过程，熟练掌握其应用方法，明确应用条件.（难点）板块一：勾股定理及其逆定理的简单应用如图，有两棵树，一棵高8m，另一棵高2m，两树相距8m，

一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少要飞______m8m2m8mABC板块二：勾股定理实际应用中常见的几个问题如图，已知CD＝6cm，AD＝8cm，∠ADC＝90o，BC＝24cm，AB＝26cm，求阴影部分面积.面积问题解：在Rt△ADC中，∵AC2=AD2+CD2（勾股定理）=

82+62=100，∴AC=10.∵AC2+BC2=102+242=676=262，∴△ACB为直角三角形(勾股定理的逆定理).∴S阴影部分=S△ACB-S△ACD=120-24=96.折叠问题如图，

在矩形ABCD中，沿直线AE把△ADE折叠，使点D恰好落在边BC上一点F处，AB＝8cm，CE=3cm，求BF的长度。ABAB如图，一圆柱高8cm，底面半径2cm，一只蚂蚁沿着圆柱表面从点A爬到点B处吃食，问蚂蚁要爬行的最短路程是多少？最短路程

问题如果圆柱换成如图长为3cm，宽为2cm，高为1cm的长方体，蚂蚁沿着表面需要爬行的最短路程又是多少呢？（计算结果保留根号）AB321分析：蚂蚁由A爬到B过程中较短的路线有多少种情况？(1)经过前面和上底

面;(2)经过前面和右面;(3)经过左面和上底面.AB23AB1C321BCA321BCA(1)当蚂蚁经过前面和上底面时，如图，最短路程为223318解:AB23AB1C22BCACAB＝＝＝(2)当蚂蚁经

过前面和右面时，如图，最短路程为22BCAC221526AB321BCAAB＝＝＝(3)当蚂蚁经过左面和上底面时，如图，最短路程为AB22BCAC222420262018AB＝＝＝321BCA最短路程为㎝1852网格问题(2)(1)(3)已知如图所示，正方形的边长都是1,如图(

1)所示,可以算出正方形的对角线长为,那么两个正方形并排所构成的矩形的对角线长为,n个正方形并排所得矩形的对角线为.(4)12n小试身手：☞“实数与数轴上的点一一对应”你能在数轴上找到表示的点吗？5通过本堂课的学习，你有何收获？点滴收获如数家珍勾股定理是几何中最重要的定理之一

，它揭示了直角三角形三边之间的数量关系。考虑问题要全面，不要漏了某些情况。学会分类讨论思想和方程思想的使用。要学会根据题意画出草图，构建直角三角形,建立数学模型解决问题。