【文档说明】2022年中考数学一轮复习习题精选《三角形（含多边形及其内角和）》(含答案).doc，共(14)页，1023.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-41671.html

以下为本文档部分文字说明：

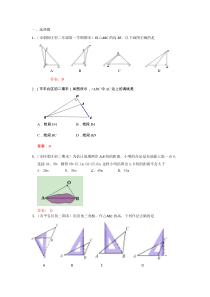
一、选择题1．（市朝阳区初二年级第一学期期末）画△ABC的高BE，以下画图正确的是ABCD答案：D2．（市丰台区初二期末）如图所示，△ABC中AC边上的高线是A．线段DAB．线段BAC．线段BCD．线段BD答案：D3．（市怀柔区初二期末）为估计池塘两岸A,

B间的距离，小明的办法是在地面上取一点O,连接OA，OB，测得OB=15.1m,OA=25.6m.这样小明估算出A,B间的距离不会大于A．26mB．38mC．40mD．41m答案：D4.（市平谷区初二期末）用直角三角板，作△

ABC的高，下列作法正确的是ABCD答案：D5.（延庆区八年级第一学区期末）如图，将ABC△放在正方形网格图中（图中每个小正方形的边长均为1），点A，B，C恰好在网格图中的格点上，那么ABC△中BC边上的高是A.102B.104C.105D.5答案：A6、

（房山区二模）如图，在△ABC中，过点B作PB⊥BC于B，交AC于P，过点C作CQ⊥AB，交AB延长线于Q，则△ABC的高是A．线段PBB．线段BCC．线段CQD．线段AQ答案：C7．（西城区九年级统一测试）如果一个正多边形的内角和

等于720，那么该正多边形的一个外角等于（）．A．45B．60C．72D．90答案：B8．（延庆区初三统一练习）利用尺规作图，作△ABC边上的高AD，正确的是答案：B9．（平谷区中考统一练习）一个正多边形的每个内角的度数都等于相邻外角的度数，

则该正多边形的边数是A．3B．4C．6D．12ABCDABCDABCDABCDA．B．C．D．答案B10．（市大兴区检测）已知一个多边形的内角和是它的外角和的2倍，那么这个多边形的边数是A.3B.4C．5D

．6答案D11．（海淀区第二学期练习）若正多边形的一个外角是120°，则该正多边形的边数是A.6B.5C.4D.3答案D12．（门头沟区初三综合练习）如图所示，有一条线段是ABC(AB>AC)的中线，

该线段是A．线段GHB．线段ADC．线段AED．线段AF答案B13．（海淀区第二学期练习）用三角板作ABC△的边BC上的高，下列三角板的摆放位置正确的是ABCD答案A二、填空题14．（延庆区初三统一练习）右图是一个正五边形，则∠

1的度数是．答案：72°15、（丰台区二模）正六边形每个内角的度数是．答案：120°16.（昌平区初二年级期末）小龙平时爱观察也喜欢动脑，他看到路边的建筑和电线架等，发现了一个现象：一切需要稳固的物品都是由三角形这个图形构成的，当时他就思考，数学王国

中不仅只有三角形，为何偏偏用三角形稳固它们呢？请你用所学的数学知识解ABCDEFG1CBAABCABCCBACBAABCABCCBACBAABCABCCBACBAABCABCCBAGHEFDABC释这一现象的依据为.答案：三角形具有稳定性17.（市朝阳区初二年级第一学期期末）如图，点D是线段

AB上一点，90CABADEABF，ACBD，ADBF，ABDE．若AEB，则CEF．（用含的式子表示）答案：900-α18、（市海淀区八年级期末）如图，在四边形ABCD中，∠A=90°，∠D=40°，则∠B+∠C为．答案：230°19、（市怀

柔区初二期末）三角形的三个内角的度数比是1:1:2.则最大内角的度数是____________．答案：90°20、.（市怀柔区初二期末）如图，△ABC中，BC边所在直线上的高是线段____________．答案

：AD21．（市门头沟区八年级期末）年11月5日19时45分，我国在西昌卫星发射中心用长征三号乙运载火箭，以“一箭双星”的方式成功发射第二十四、二十五颗北斗导航卫星．这两颗卫星属于中圆地球轨道卫星，是我国北斗三号第一、二GEDCBA颗组网卫星，开启了北

斗卫星导航系统全球组网的新时代．如图所示，在发射运载火箭时，运载火箭的发射架被焊接成了许多的三角形，这样做的原因是：．答案：略22.（市顺义区八年级期末）已知：ABC中，ABAC，30BA，则A.答案：

4023．（市顺义区八年级期末）将一副直角三角板如图放置，使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合，则∠1的度数为度．答案：7524．（市顺义区八年级期末）已知:如图，ABC△中，45ABC，H是高AD和BE的交点，12AD,17BC

，则线段BH的长为.答案：1325．（石景山区初三毕业考试）若正多边形的一个外角是45°，则该正多边形的边数是_______．答案：八26、（昌平区二模）10.如图，∠1是五边形ABCDE的一个外角．若∠1＝60°，则∠A＋∠B＋∠C＋∠D的度数为_________

．HECDBA答案：420°27．（东城区一模）若多边形的内角和为其外角和的3倍，则该多边形的边数为________________.答案8三、解答题28．（延庆区初三统一练习）如图，在△ABC中，AD平分∠BAC交BC于点D，过点D作DE∥AB交AC于点E．求

证：AE=DE．证明：∵AD平分∠BAC∴∠BAD=∠DAE，∵DE∥AB∴∠BAD=∠ADE……3分∴∠DAE=∠ADE……4分∴AE=DE……5分29．（市朝阳区一模）如图，BD是△ABC的角平分线，DE//BC交AB于点E．（1）求证：BE=DE；（2）若AB=BC=10，求DE的长．解

（1）证明：∵BD是△ABC的角平分线，∴∠EBD=∠CBD．∵DE//BC，∴∠EDB=∠CBD.∴∠EDB=∠EBD．∴BE=DE．„„„„„„„„„„„„„„„„„„„„2分EDCBA（2）解：∵AB

=BC，BD是△ABC的角平分线，∴AD=DC．„„„„„„„„„„„„„„„„„„„„„„3分∵DE//BC，∴1DCADEBAE．„„„„„„„„„„„„„„„„„„„„„4分∴521ABBE．∴5DE．„„„„„„„„„„„„„„„„„„„„„5分

30.（市朝阳区综合练习（一））如图，在△ACB中，AC=BC，AD为△ACB的高线，CE为△ACB的中线.求证：∠DAB=∠ACE.∴∠CAB＝∠B，CE⊥AB.„„„„„„„„„„„„„„„2分∴∠CAB＋∠ACE＝90°.„„„„„„„„„„„

„„„„„3分∵AD为△ACB的高线，∴∠D＝90°.∴∠DAB＋∠B＝90°.„„„„„„„„„„„„„„„4分∴∠DAB＝∠ACE.„„„„„„„„„„„„„„„„„„„5分31．（门头沟区初三综合练习）如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于E，∠BAC

＝60°，∠ABE＝25°.求∠DAC的度数.解∵BE平分∠ABC，∴∠ABC=2∠ABE=2×25°=50°，„„„2分∵AD是BC边上的高，∴∠BAD=90°﹣∠ABC=90°﹣50°=40°，„„„„4分∴∠DAC=∠BAC﹣∠BAD=60°﹣40

°=20°„„„„„„5分32.（通州区一模）EDABC答案：33．（市大兴区检测）如图，在△ABC中，AB=AC，点D，点E分别是BC，AC上一点，且DE⊥AD.若∠BAD=55°，∠B=50°，求∠DEC的度数．解：∵AB=AC，∴∠

B=∠C．∵∠B=50°，∴∠C=50°．……………………1分∴∠BAC=180°-50°-50°=80°．…………………………………………………2分∵∠BAD=55°，∴∠DAE=25°．…………………………………………………………………3分∵DE⊥AD，∴∠ADE=90°．………………………

…………………………………………4分∴∠DEC=∠DAE+∠ADE=115°．………………………………………………5分34.（东城区一模）如图，在△ABC中，∠BAC=90°，AD⊥BC于点D.BF平分∠ABC交AD于点E，交AC于点F.求证：AE=AF.证明：∵∠

BAC=90°，∴∠FBA+∠AFB=90°.-------------------1分∵AD⊥BC，∴∠DBE+∠DEB=90°．----------------2分∵BE平分∠ABC,∴∠DBE=∠FBA.------

-------------3分∴∠AFB=∠DEB.-------------------4分∵∠DEB=∠FEA，∴∠AFB=∠FEA.∴AE=AF.-------------------5分35．（市

朝阳区初二年级第一学期期末）已知：如图，点D，E在ABC的边BC上，ABAC，ADAE．求证：BDCE．证明：过点A作AHBC于点H．„„„„„„„„„„„„„„„„„„1分∵ABAC，ADAE，∴HBHC

，HDHE．„„„„„„„„„„„„„„„„„3分∴HBHDHCHE．即BDCE．„„„„„„„„„„„„„„„„„„„„5分36．（市朝阳区初二年级第一学期期末）在等边ABC外作射线AD，使得AD和AC在直线AB的两侧，BAD（0180），点B关于

直线AD的对称点为P，连接PB，PC．（1）依题意补全图1；（2）在图1中，求BPC的度数；EDCBA（3）直接写出使得PBC是等腰三角形的的值．解：（1）补全的图形如图所示．„„„„„„„„„„„„1分（2）解：连接AP，如图．由点B关于直线AD的对称点为P，

可得AD垂直平分PB．∴APAB．∴PADBAD．∵ABC是等边三角形，∴ABAC，60BAC．∴APAC．„„„„„„„„„„„„„„„„„„„„„„„„2分∴APCACP．∴在APC中，22180APCPADBAC．∴60

APCPAD．∴30BPC．„„„„„„„„„„„„„„„„„„„„„„3分（3）30，75，120，165．„„„„„„„„„„„„„„„„„7分37.（市东城区初二期末）如图，在△ABC

中，AB＝AC，AD⊥于点D，AM是△ABC的外角∠CAE的平分线．(1)求证：AM∥BC；(2)若DN平分∠ADC交AM于点N，判断△ADN的形状并说明理由．CBA备用图图1DCBAPDCBAPDCBAABCPABCPNDBCAEM

解：（1）∵AB=AC，AD⊥BC，∴∠BAD=∠CAD=12BAC．„„„„„1分∵AM平分∠EAC，∴∠EAM=∠MAC=12EAC．„„„„„2分∴∠MAD=∠MAC+∠DAC=1122EACB

AC=1180902。∵AD⊥BC∴90ADC∴∠MAD+180ADC∴AM∥BC.。„„„„„3分（2）△ADN是等腰直角三角形„„„„„4分理由是：∵AM∥AD∴∠AND=

∠NDC，∵DN平分∠ADC，∴∠ADN=∠NDC=∠AND.∴AD=AN．„„„„„6分∴△ADN是等腰直角三角形．38．（市丰台区初二期末）如图，△ABC中，∠ACB＝90°，AC＝BC．在△ABC外侧作直线CP，点A关于直线CP

的对称点为D，连接AD，BD，其中BD交直线CP于点E．图1图2（1）如图1，∠ACP＝15°.①依题意补全图形；②求∠CBD的度数；（2）如图2，若45°<∠ACP<90°，直接用等式表示线段AC，DE，BE之间的数量关系．答案：39．（市海淀区八年级期末）如图，A，B分别为CD，C

E的中点，AE⊥CD于点A，BD⊥CE于点B．求∠AEC的度数．解：连接DE．----------------------------------------------1分∵A，B分别为CD，CE的中点，AE⊥CD于点A，BD⊥CE于点B，∴CD=CE=DE，∴△CDE为等边三

角形．----------------------------3分∴∠C=60°．∴∠AEC=90°12∠C=30°．----------------------5分40．（市西城区八年级期末附加题）在平面直角坐标系xOy中，直线l1：12yxb与x轴交于点A，

与y轴交于点B，且点C的坐标为（4，4）．（1）点A的坐标为，点B的坐标为；（用含b的式子表示）（2）当4b时，如图1所示．连接AC，BC，判断△ABC的形状，并证明你的结论；EDCBAEDCBA（3）过点C作平行于y轴的直线l2

，点P在直线l2上．当54b时，在直线l1平移的过程中，若存在点P使得△ABP是以AB为直角边的等腰直角三角形，请直接写出所有满足条件的点P的纵坐标．解：（1）（2b，0），（0，b）；„„„„„„„„„„„„„„„„„„„„„2分（

2）等腰直角三角形；„„„„„„„„„„„„„„„„„„„„„„„3分证明：过点C作CD⊥y轴于点D，如图，则∠BDC=∠AOB=90°．∵点C的坐标为（4，4），∴点D的坐标为（0，4），CD=

4．∵当b=4时，点A，B的坐标分别为（8，0），（0，4），∴AO=8，BO=4，BD=8．∴AO=BD，BO=CD．在△AOB和△BDC中，AO=BD，∠AOB=∠BDC，BO=CD，∴△AOB≌△BDC．„„„„„„„„„„„„„„„„„„„4分∴∠1=∠2，

AB=BC．∵∠1+∠3=90°，∴∠2+∠3=90°，即∠ABC=90°．∴△ABC是等腰直角三角形．„„„„„„„„„„„„„„„5分（3）12，83，8．„„„„„„„„„„„„„„„„„„„„„„„„8分备用图图1