【文档说明】2022年中考数学一轮复习第22课《圆的基本性质》知识梳理练习 (含答案).doc，共(7)页，358.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-41643.html

以下为本文档部分文字说明：

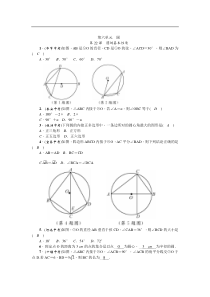
第六单元圆第22课圆的基本性质1．(毕节中考)如图，AB是⊙O的直径，CD是⊙O的弦，∠ACD＝30°，则∠BAD为(C)A．30°B．50°C．60°D．70°2．(泰安中考)如图，△ABC内接于⊙O，若∠A＝α，则∠OBC等于(D)A．180°－2αB．2αC．9

0°＋αD．90°－α3．(株洲中考)下列圆的内接正多边形中，一条边所对的圆心角最大的图形是(A)A．正三角形B．正方形C．正五边形D．正六边形4．(宜昌中考)如图，四边形ABCD内接于⊙O，AC平分∠BAD，则下列结论正确的是(B)A．AB＝ADB．BC＝CDC.AB︵＝AD︵D．∠BCA＝∠

DCA5．(河池中考)如图，⊙O的直径AB垂直于弦CD，∠CAB＝36°，则∠BCD的大小是(B)A．18°B．36°C．54°D．72°6．到定点O的距离为3cm的点的集合是以点__O__为圆心，__3__cm__为半径的圆．7．(十堰中考)如图，△ABC内接于⊙O，∠A

CB＝90°，∠ACB的角平分线交⊙O于点D.若AC＝6，BD＝52，则BC的长为__8__．8．(东营中考)如图，AB是半圆直径，半径OC⊥AB于点O，D为半圆上一点，AC∥OD，AD与OC交于点E，连接CD、BD，给出以下三个结论：①OD平分∠COB

；②BD＝CD；③CD2＝CE·CO，其中正确结论的序号是__①②③__．9．(毕节中考)正六边形的边长为8cm，则它的面积为__963__cm2.10．(绥化中考)半径为2的圆内接正三角形、正四边形、正六边形的边心距之比为__1∶2∶3__．11．(西宁中考)如图，四边形ABCD内接于⊙O，点E

在BC的延长线上，若∠BOD＝120°，则∠DCE＝__60°__．12．如图，已知AB是⊙O的弦，点C在线段AB上，OC＝AC＝4，CB＝8.求⊙O的半径．解：连接OA，过点O作OD⊥AB于点D.∵AC＝4，CB＝8，∴AB＝12.∵OD⊥AB，∴AD＝DB＝6，∴CD＝2.在

Rt△CDO中，∠CDO＝90°，∴OD＝OC2－CD2＝23.在Rt△ADO中，∠ADO＝90°，由勾股定理，得OA＝（23）2＋62＝43，即⊙O的半径是43.13．(株洲中考)如图所示，AB为⊙O的一条弦，点C为劣弧AB︵的中点，E为优弧AB︵上一点，点F在AE的延长线上，且BE＝EF

，线段CE交弦AB于点D.(1)求证：CE∥BF；(2)若BD＝2，且EA∶EB∶EC＝3∶1∶5，求△BCD的面积．(注：根据圆的对称性可知OC⊥AB)解：(1)连接AC.∵BE＝EF，∴∠F＝∠EBF.∵∠AEB＝∠EBF＋∠F，∴∠F＝12∠AEB.∵C是AB︵的中点

，∴AC︵＝BC︵，∴∠AEC＝∠BEC.∵∠AEB＝∠AEC＋∠BEC，∴∠AEC＝12∠AEB.∴∠AEC＝∠F，∴CE∥BF；(2)作直线OC交AB于点G，∵∠DAE＝∠DCB，∠AED＝∠CEB，∴△ADE∽△CBE，∵EA∶EB∶

EC＝3∶1∶5，∴ADCB＝AECE＝35，∵∠CBD＝∠AEC＝12∠AEB＝∠CEB，∠BCD＝∠ECB，∴△CBE∽△CDB，∴BDCB＝BECE，即2CB＝15，∴CB＝25，∴AD＝6，∴AB＝8.∵点C为劣弧AB的中点，∴OC⊥AB，AG＝BG＝12

AB＝4，∴CG＝CB2－BG2＝2，∴△BCD的面积＝12BD·CG＝12×2×2＝2.14．如图，在⊙O中，CD为⊙O的直径，AC︵＝BC︵，点E为OD上任意一点(不与O，D重合)．求证：AE＝BE.证明：∵AC︵＝BC︵，∴∠AOC＝∠BOC，∴∠AOE

＝∠BOE.∵OA，OB是⊙O的半径，∴OA＝OB.又OE＝OE，∴△AOE≌△BOE(SAS)，∴AE＝BE.15．(郴州中考)如图，AB是⊙O的弦，BC切⊙O于点B，AD⊥BC，垂足为点D，OA是⊙O的半径，且

OA＝3.(1)求证：AB平分∠OAD；(2)若点E是优弧AEB︵上一点，且∠AEB＝60°，求扇形OAB的面积．(计算结果保留π)解：(1)连接OB.∵BC切⊙O于点B，∴OB⊥BC.∵AD⊥BC，∴AD∥

OB，∴∠DAB＝∠OBA.∵OA＝OB，∴∠OAB＝∠OBA，∴∠DAB＝∠OAB，∴AB平分∠OAD；(2)∵E是优弧AEB︵上一点，且∠AEB＝60°，∴∠AOB＝2∠AEB＝120°，∴S扇形OAB＝120π×

32360＝3π.16．(台州中考)如图，已知等腰直角三角形ABC，点P是斜边BC上一点(不与B，C重合)，PE是△ABP的外接圆⊙O的直径．(1)求证：△APE是等腰直角三角形；(2)若⊙O的直径为2，求PC2＋PB2的值．解：(1)∵AB＝AC，∠BAC＝90°，

∴∠C＝∠ABC＝45°，∴∠AEP＝∠ABP＝45°，∵PE是直径，∴∠PAB＝90°，∴∠APE＝∠AEP＝45°，∴AP＝AE，∴△PAE是等腰直角三角形；(2)作PM⊥AC于M，PN⊥AB于N，则四边形PMAN是矩形，∴PM＝AN，∵△PCM，△PNB都是等腰直角三角形，∴

PC＝2PM，PB＝2PN，∴PC2＋PB2＝2(PM2＋PN2)＝2(AN2＋PN2)＝2PA2＝PE2＝22＝4.