【文档说明】2021年人教版高中数学选择性必修第二册（精讲)拓展二《数列求和的方法》（解析版）.doc，共(18)页，1.399 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38168.html

以下为本文档部分文字说明：

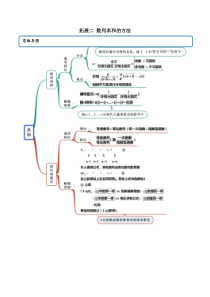
拓展二数列求和的方法思维导图常见考法考点一裂项相消【例1】（2020·云南弥勒市一中月考（理））若数列na的前n项和nS满足2nnSan.(1)求证：数列1na是等比数列；(2)设2log1nnba，求数列11nnbb的前

n项和nT.【答案】（1）详见解析（2）1nnTn【解析】证明：当1n时，11121aSa，计算得出11a，当1n时，根据题意得，1121nnSan，所以111221221nnnnnnSSananaa，即121n

naa1121nnaa，即1121nnaa数列1na是首项为-2，公比为2的等比数列由（1）知，11222nnna12nna22log1

log2nnnban1111111nnbbnnnn，1则1111111...1311122nnnnnnT【一隅三反】1．（2020·湖南天心·长郡中学月考（文））设数列na

满足：11a，且112nnnaaa（2n），3412aa.（1）求na的通项公式：（2）求数列21nnaa的前n项和.【答案】（1）21nan（*nN）（2）113(21)(23)

nnn【解析】(1)由112nnnaaa(2n)可知数列na是等差数列,设公差为d,因为11a,所以34112312aaadad,解得2d,所以na的通项公式为:21nan(*nN);(2)由(1)知211111(21)(23)4212

3nnaannnn,所以数列21nnaa的前n项和:1111111114537592123nSnn11111432123nn113(21)(

23)nnn.2．（2020·石嘴山市第三中学月考）已知na是公差不为零的等差数列，11a，且139,,aaa成等比数列.（1）求数列na的通项公式；（2）求数列11nnaa的前n项和nS.【答案】（1）nan，（2）1nnSn【解析】（1）设等

差数列na的公差为d（0d），因为11a，且139,,aaa成等比数列，所以2319aaa，即2(12)1(18)dd，解得0d（舍去）或1d，所以nan，（2）由（1）可得11111(1)1nn

aannnn，所以111111+2231nnnS1111nnn考点二错位相减【例2】．（2020·贵州省思南中学月考）已知

数列{}na满足1(1)nnnana，且11a（1）求数列{}na的通项公式；（2）设2nnnba，求数列{}nb的前n项和nS.【答案】（1）nan；（2）1*(1)22,()nnSnnN.【解析】（1）11nnanan

2n时，有32412312341231nnaaaanaaaan，即1nana，故nan，又1n时也适合该式，nan（2）因为2nnbn，所以1231222322nnSn①则234121222

322nnSn②①-②得，123112(12)22222212nnnnnSnn1*(1)22,()nnSnnN.【一隅三反】1．（2020·赣榆智贤中学月考）已知数列na是公差0d的等差数列，其

前n项和为nS，满足42210Sa，且1a，2a，5a恰为等比数列nb的前三项．（1）求数列na，nb的通项公式；（2）设nnnacb，数列nc的前n项和为nT，求证：3nT．【答案】（1）21nan，13nnb；（2）见解析【解析】（1）由题意，

422215210Saaaa，得121252addad，由0d，得11a，2d．所以21nan．由11b，23b，得公比3q，所以13nnb．（2）因为1213nnnc，所以012113

5213333nnnT①得23111352321333333nnnnnT②①-②得21222221133333nnnnT12113321221213313nnnnn．所以333

3nnnT．从而3nT．2．（2020·江苏泗阳·桃州中学月考）设数列na、nb都有无穷项，na的前n项和为21352nSnn，nb是等比数列，34b且632b.（1）求na和nb的通项公式；（2）记nnnacb，求数列nc的前n项和为nT.【

答案】（1）31nan；1*,2nnbnN（2）137142nn【解析】（1）当1n时，1a=1S=4；当2n时，22111353(1)5(1)22nnnaSSnnnn1[3(21)5]312n

n，且14a亦满足此关系，∴na的通项为*31,nannN，设nb的公比为q，则3638bqb，则2q=，∴31*32nnnbbqnN；（2）由题意，1312nnn

nancb，而214710323112422nnnnnT，27101331281242nnnT，两式相减，有21111318312422nnnnT，21

11313783214222nnnnn．3．（2020·江苏泗阳·桃州中学月考）已知数列na满足121nnaa()nN，12a.（1）求数列na的通项公式；（2）求数列nna的前n项和nS

()nN.【答案】（1）121nna；（2）(1)(1)212nnnnSn．【解析】（1）∵121nnaa，∴112(1)nnaa，而1110a，∴数列{1}na是等比数列，公比为1，首项为1，

∴112nna，∴121nna；（2）由（1）11212nnnnannn，21(111)(222)(323)(2)nnSnn21(1122322)(123)nnn

设21122322nnTn，则2312122232(1)22nnnTnn，两式相减得2112222212nnnnnTnn，∴(1)21nnTn，∴(1)(1)212nnnnSn

．考点三分组求和【例3】．（2020·赣榆智贤中学月考）已知等差数列na的前n项和为nS，等比数列nb的前n项和为nT.若113ab，42ab，4212ST.（1）求数列na与nb的通项公式；（

2）求数列nnab的前n项和.【答案】（1）213nnnanb，（2）33122nnn【解析】（1）由11ab,42ab，则421234122312STaaaabbaa

，设等差数列na的公差为d，则231236312aaadd，所以2d，所以3(1)21nandn设等比数列nb的公比为q由4219,3abb，2139bbqq，解得3q，所

以113nnnbbq，（2）213nnnabn，数列nnab的前n项和22222naaabbb231332135213332213nnnnnnn3312n【一隅三反】1

．（2020·河南高二月考）已知数列nc的前n项和122nnT，在各项均不相等的等差数列nb中，11b，且1b，2b，5b成等比数列，（1）求数列nb、nc的通项公式；（2）设22lognbnnac，求数列na的前n项和nS．【答案】（1）1121n

bbndn，2nnc；（2）nS2122232nnn．【解析】（1）设数列nb的公差为d，则21bbd，514bbd，∵1b，2b，5b成等比数列，∴2215bbb，即21114bdbbd．整理得212dbd，解得0d（舍去

）或122db，∴1121nbbndn．当1n时，12c，当2n时，1112222222222nnnnnnnnnncTT．验证：当1n时，12c满足上式，∴数列nc的通项公式为2nn

c．（2）由（1）得，2122log2nbnnnacn，∴35212122232nnSn35212222123nn21221412214232nnnnnn

．2．（2020·河南高二月考（理））已知在等比数列na中，11a，且2a是1a和31a的等差中项.（1）求数列na的通项公式；（2）若数列nb满足*2nnbnanN，求nb的前n项和

nS.【答案】（1）12nna-=；（2）221nnSnn.【解析】（1）设等比数列na的公比为q，则0q，则21aaqq，2231aaqq，由于2a是1a和31a的等差中项，即21321aaa，即22qq，解得2

q=.因此，数列na的通项公式为1111122nnnnaaq；（2）1222nnnbnan，012112322426222nnnSbbbbn212

(22)12(2462)122221212nnnnnnnn.3．（2020·天水市第一中学）已知等比数列na的各项均为正数，22a，3412aa.（1）求数列na的通项公式；（2）设2lognnnbaa，求数列nb的前n项和

nS.【答案】（1）12nna-=（2）(1)212nnnnS【解析】（1）设公比为q由题意可知12311212aqaqaq，整理得260qq，解得3q（舍），2q=，即11a则11122nnna

（2）11122log221nnnnbn12(1)(1)211222nnnnnnnS考点四倒序相加【例4】．（2020·全国高三其他（文））已知函数coslnxfxxx，若22018201920192019fff

1009ln0,0)abab（，则11ab的最小值为（）A．2B．4C．6D．8【答案】A【解析】由题可知：2coslncoslnln2lnxxfxfxxxxx

令22018201920192019Sfff又20182017201920192019Sfff于是有22ln2ln2

ln22018lnS2018lnS因此2ab所以11111112222222ababababba当且仅当1ab时取

等号本题正确选项：A【一隅三反】1．（2020·江苏高二期中）设函数221xfx，利用课本（苏教版必修5）中推导等差数列前n项和的方法，求得54045fffff的值为（）A．9B．11C．

92D．112【答案】B【解析】221xfx，22222212121221xxxxxxfxfx2122222211221xxxxx，设54045Sffff

f，则54045Sfffff，两式相加得2115511222Sff，因此，11S.故选：B.2．（2019·浙江丽水·高二月考）已知函数si

n3fxxx，则12340332017201720172017ffff的值为（）A．4033B．-4033C．8066D．-8066【答案】D【解析】2sin32sin234fxfxxxxx

，所以原式4033480662.3．（2020·江苏常熟中学月考）已知函数442xxfx，设2019nnaf（nN），则数列na的前2019项和2019S的值为（）A．30293B．30323

C．60563D．60593【答案】A【解析】因为442xxfx，所以114214242xxxfx所以21414242xxxfxfx因为2019nnaf所以2019nnaf，20192019120192019nnnffa

所以20191nnaa则数列na的前2018项和2018S则1220182018aaSa2018212018017Saaa所以201820182S所以20181009S又9120112011942201942

3aff20192018201923029100933SSa故选：A考点五奇偶并项【例5】．（2020·湖南高二月考）设*Nn，数列na的前n项和为nS，已知12nnnSSa，______.请

在①1a，2a，5a成等比数列，②69a，③535S，这三个条件中任选一个补充在上面题干中，并解答下面问题.（1）求数列na的通项公式；（2）若数列nb满足121nannnba，求数列nb的前2

n项的和2nT.【答案】（1）答案见解析；（2）答案见解析.【解析】选①，（1）由12nnnSSa得：*12Nnnaan，∴数列na是以1a为首项，2为公差的等差数列.由1a，2a，5a成等比数列得211128aaa，解得11a.∴

*21Nnann.（2）1212121nannnnnban，22122211357...434122221nnnTnnn.选②，（1）由12nnnSSa

得*12Nnnaan，∴数列na是以1a为首项，2为公差的等差数列.由69a得1529a，解得11a，∴*23Nnann.（2）11212123nannnnnban，∴2221

1135...454321nnTnn2212412nnnn.选③，（1）同理，由12nnnSSa得*12Nnnaan，∴数列na是以1a为首项，2为公差的等差数列

，由535S得151035ad，解得13a，∴*21Nnann.（2）11212121nannnnnban，∴2222213579...414121nnTnn221242442nnnn

.【一隅三反】．1（2019·广东汕头·金山中学高二月考（理））设nS是数列na的前n项和，已知11a，122nnSa⑴求数列na的通项公式；⑵设121lognnnba，求数列

nb的前n项和nT．【答案】（1）112nna（2）1,2,2nnnTnn为奇数为偶数【解析】（1）因为122nnSa，所以当2n时，122nnSa两式相减得122nnnaaa

，所以112nnaa当1n时，1222Sa，11a，则212a所以数列na为首项为1，公比为12的等比数列，故112nna（2）由（1）可得121log11nnnnban所以012311nnTn

故当n为奇数时，101234212nnTnn当n为偶数时，012345212nnTnn综上1,2,2nnnTnn为奇数为偶数2．（

2020·内蒙古集宁一中期中（理））已知数列na的前n项和为,239nnnSSa．(1)求数列na的通项公式；(2)若31lognnnba，求数列nb的前n项和nT．【答案】（1）13nna；（2）,23,2nnnTnn为偶数为奇数【解析】（1

）当1n时，11239Sa.因为11Sa，所以11239aa，所以19a.因为239nnSa，所以11239nnSa.两式相减，得11233nnnaaa，即13nnaa又因为19a，所以0na.所以数列na是以9为首项，3为公比的等比数列.所

以11933nnna.（2）由（1）可知31log11nnnnban故当n为偶数时，234512nnTnn当n为奇数时，123451112nnTnnnn

32n所以,23,2nnnTnn为偶数为奇数考点六绝对值求和【例6】．（2020·鄂尔多斯市第一中学高二期中（理））已知数列na的通项公式100nann，则122399100aaaaaa（）A

．150B．162C．180D．210【答案】B【解析】由对勾函数的性质可知：当10n时，数列na为递减；当10n≥时，数列na为递增．所以122310099aaaaaa=1223

9101110121110099()()()()()()aaaaaaaaaaaa=11010010aaaa=1100(1010)(1001)(1010)=162【一隅三反】1．（2020·广东宝安·高二期末）已知na是首项为32的等比数列，nS是其

前n项和，且636564SS，则数列2logna前10项和为()A．58B．56C．50D．45【答案】A【解析】na是首项为32的等比数列,nS是其前n项和,且636564SS,所以公比不为1，63321651643211qqqq,3

65164q,14q,172132()24nnna,2log72nan,数列2logna前10项和为53113579111358,故选：A